Последовательность натуральных чисел.

Рассмотрим некоторое множество (класс) множеств 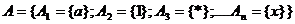, каждое из которых содержит по одному элементу. Любое натуральное число – это характеристика класса равносильных конечных множеств, тогда поставим в соответствие этому классу натуральное число «единица» и обозначим его символом «1». Выберем из данного класса любое «единичное» множество, пусть 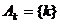, и добавим в это множество еще один элемент, получим новое множество 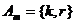. Если образовать класс конечных множеств, равносильных множеству 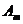, то новому классу поставим в соответствие натуральное число «два» и обозначим его символом «2». Дальнейшее продолжение этого бесконечного процесса образования новых конечных множеств и соответствующих им классов приводит к образованию двух бесконечных последовательностей:

(а) бесконечной последовательности множеств 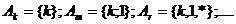(1); каждое из этих множеств служит представителем соответствующего класса;

(b) бесконечной последовательности натуральных чисел 1;2;3;…r…(2), каждое из этих чисел являются характеристикой соответствующего класса.

Сравнение последовательностей (1) и (2) приводит к следующим выводам:

1). В (1) есть начальный элемент 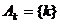и в (2) есть начальный элемент 1;

2). В (1) за каждым множеством непосредственно следует единственное множество, в котором на один элемент больше, чем в множестве предыдущего класса, поэтому в (2) за каждым натуральным числом непосредственно следует только одно натуральное число, большее предыдущего на единицу.

3). В (1) каждый класс, кроме начального, непосредственно следует только за одним классом, поэтому в (2) каждое натуральное число, кроме единицы, непосредственно следует только за одним натуральным числом.

4). В (1) каждое множество данного класса является либо подмножеством любого множества следующего за ним класса, либо равносильно подмножеству любого множества следующего за ним класса, поэтому в (2) натуральные числа расположены так, что каждое из них меньше любого, следующего за ним: 1<2<3<…..<n<n+1<… (3).

Опираясь нам основные положения метода математической индукции, можно утверждать, что (2) – это последовательность натуральных чисел.

3. Использование последовательности натуральных чисел для определения численности конечного множества.

Определить численность конечного множества – это значит сосчитать количество элементов в этом множестве, для такого подсчета используется понятие отрезка .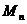

Опр. 4. Отрезком 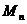последовательности (2) называется множество первых натуральных чисел последовательности (2), не превосходящих числа «n».

Пример. .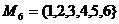

Для определение численности, например, множества 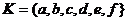приведем последовательность его элементов во взаимно однозначное соответствие с элементами отрезка :

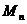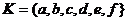
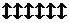
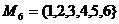. Так как 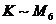, то множеству К можно поставить в соответствие число «6», это число называют числом элементов множества K: n(K)=6, говорят, что число «6» выражает численность множества К.

Опр. 5. Счетомэлементов множества 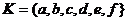называется процесс приведения во взаимно однозначное соответствие элементов множества К с элементами отрезка натурального ряда .

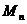При пересчете элементов конечного множества натурального ряда чисел выясняется не только количество элементов множества, но и определяется порядок расположения элементов в множестве. В первом случае натуральное число «n» показывает, сколько элементов содержит множество, «n» - называется количественнымчислом. Во втором случае натуральное число «n» представляет собой порядковый номер некоторого элемента множества, оно называется порядковым числом.

4. Операция сложения чисел в множестве N.

В множестве N натуральных чисел, кроме отношений равенства и неравенства, вводятся ряд операций. Каждую из операций можно ввести теорию на основе теории множеств.

Опр.6. Суммой двух данных натуральных чисел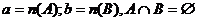

называется натуральное число 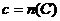, где .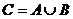

Обозначается: 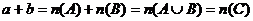, a,b – слагаемые, с – сумма.

Замечание:Определение суммы двух натуральных чисел можно распространить на любое их число.

Операция нахождения суммы двух чисел (сложение чисел) обладает рядом свойств:

1) Сумма двух натуральных чисел 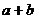существует и единственна (доказательство этого свойства суммы, как и последующих свойств, опирается на свойства операций с множествами).

2) 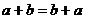- 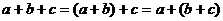свойство переместительности (коммутативности) суммы;

3) 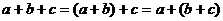- свойство сочетательности (ассоциативности) суммы;

4) 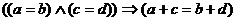- свойство аддитивности суммы ( при сложении равных чисел получаем равные суммы);

5) 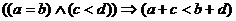, 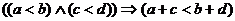- свойство монотонности суммы (при сложении неравных чисел получаем неравные числа того же смысла).