Вывод параметрических уравнений прямой на плоскости.
В разделе способы задания прямой линии на плоскости мы показали, что конкретную прямую можно определить, если указать принадлежащую ей точку и направляющий вектор прямой.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Зададим прямую a, указав лежащую на прямой a точку 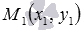 и направляющий вектор этой прямой
и направляющий вектор этой прямой 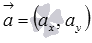 . Опишем прямую a с помощью уравнений.
. Опишем прямую a с помощью уравнений.
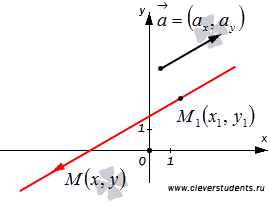
Возьмем произвольную точку плоскости 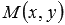 . Мы можем вычислить координаты вектора
. Мы можем вычислить координаты вектора 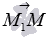 по координатам точек его начала и конца:
по координатам точек его начала и конца: 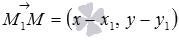 . Очевидно, что множество всех точек
. Очевидно, что множество всех точек 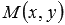 задают прямую, проходящую через точку
задают прямую, проходящую через точку 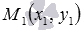 и имеющую направляющий вектор
и имеющую направляющий вектор 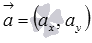 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 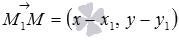 и
и 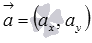 коллинеарны.
коллинеарны.
Необходимое и достаточное условие коллинеарности векторов 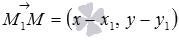 и
и 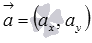 записывается в виде уравнения
записывается в виде уравнения 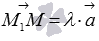 , где
, где 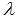 - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой. Векторно-параметрическое уравнение прямой в координатной форме имеет вид
- некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой. Векторно-параметрическое уравнение прямой в координатной форме имеет вид 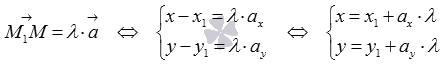 . Уравнения полученной системы
. Уравнения полученной системы 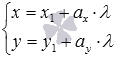 называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy. Смысл такого названия прост: координаты всех точек прямой могут быть вычислены по параметрическим уравнениям прямой на плоскости вида
называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy. Смысл такого названия прост: координаты всех точек прямой могут быть вычислены по параметрическим уравнениям прямой на плоскости вида 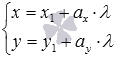 при переборе всех действительных значений параметра
при переборе всех действительных значений параметра 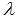 .
.
| Взаимное расположение двух прямых в пространстве |
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
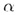 , а прямая с пересекает , а прямая с пересекает  в точке N. Прямые a и с — скрещивающиеся. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой. в точке N. Прямые a и с — скрещивающиеся. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой. 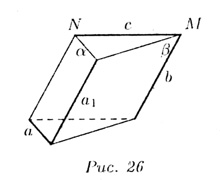 На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость 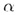 || b (в плоскости указана прямая a1 || b). Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты. || b (в плоскости указана прямая a1 || b). Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты. |
| Взаимное расположение прямой и плоскости в пространстве (формулировки и примеры) |
Прямая и плоскость в пространство могут:
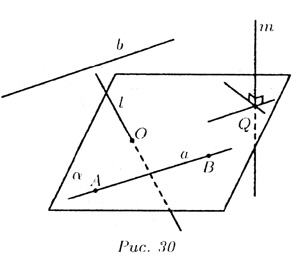 На рис. 30 изображены все эти возможности. В случае а) прямая b параллельна плоскости На рис. 30 изображены все эти возможности. В случае а) прямая b параллельна плоскости 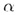 : b || : b || 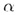 . В случае б) прямая l пересекает плоскость . В случае б) прямая l пересекает плоскость 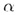 в одной точке О; l в одной точке О; l 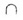 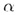 = О. В случае в) прямая а принадлежит плоскости = О. В случае в) прямая а принадлежит плоскости 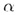 : : 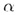 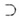 а или а а или а  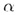 . Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости . Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости 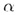 , то прямая параллельна плоскости , то прямая параллельна плоскости 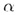 . Предположим, что прямая m пересекает плоскость . Предположим, что прямая m пересекает плоскость 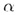 в точке Q.Если m перпендикулярна каждой прямой плоскости в точке Q.Если m перпендикулярна каждой прямой плоскости 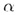 , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости 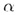 . Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные). . Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные). |
