Взаимное расположение двух линий

Чётность

Основная статья: Нечётные и чётные функции

• Функция 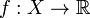называется нечётной, если справедливо равенство

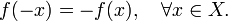
• Функция f называется чётной, если справедливо равенство

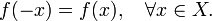
Ограниченность функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что

m ≤ f(x) ≤ M

при хє(a,b).

Число m_o= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,

а число M_o= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).

Разность M_o- m_o называется колебанием функции на промежутке (a,b).

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

9. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая).

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

• алгебраические:
• степенная;
• рациональная.
• трансцендентные:
• показательная и логарифмическая;
• тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Постоянная функция.

Постоянной называется функция, заданная формулой у = b, где b - некоторое число.

Графиком постоянной функции у = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рисунке изображены графики нескольких постоянных функций. В частности, графиком функции y = 0 является ось абсцисс.

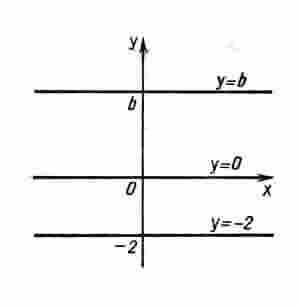
Если b = 0, то получаем прямую пропорциональность у = kх.

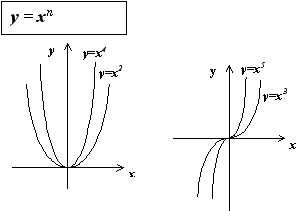
Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

Показательная функция — математическая функция 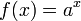, где a называется «основанием», а x — «показателем» степени.

• В вещественном случае основание степени 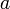— некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.
• В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
• В самом общем виде — u^v, введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

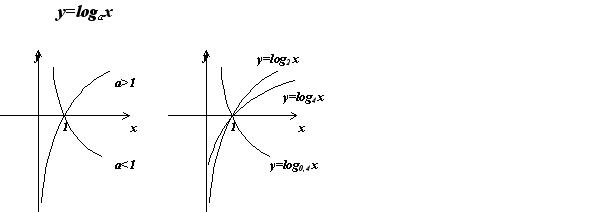
Функцияy=log_a х(гдеа> 0,а$$\ne$$1) называется логарифмической.

Построение графиков. График логарифмической функции log_aх можно построить, воспользовавшись тем, что функция log_aх обратна показательной функции y = a^x. Поэтому достаточно построить график функции y = a^x, а затем отобразить его симметртрично относительно прямой у = х.

Свойства функции у = logaх , a > 1: 1. D(f) = (0; +$$\infty$$); 2. не является ни четной, ни нечетной; 3. возрастает на (0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. не имеет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-$$\infty$$;+ $$\infty$$); 8. выпукла вверх; дифференцируема.	Свойства функцииу= logaх, 0 <a< 1 : 1. D(f) = (0;+$$\infty$$ ); 2. не является ни четной, ни нечетной; 3. убывает на (0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. нет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-;$$\infty$$+ $$\infty$$); 8. выпукла вниз; дифференцируема.
Свойства функции у = ln х : 1. D(f) = (0; +$$\infty$$); 2. не является ни четной, ни нечетной; 3. возрастает на {0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. не имеет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-$$\infty$$;+ $$\infty$$); 8. выпукла вверх; дифференцируема.

10. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести).

Определение. Уравнением линии (кривой) на плоскости 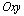называется уравнение, 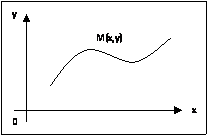которому удовлетворяют координаты и каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Если точка 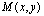передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты 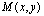называются текущими координатами.

Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию. Например: 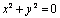определяет только одну точку (0;0); 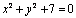не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю. Чтобы убедится, лежит ли точка 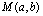на данной линии 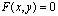, надо проверить, удовлетворяют ли координаты этой точки уравнению.

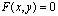Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.

Уравнение пучка прямых

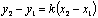
Уравнение прямой в отрезках

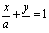
11. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.

Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.
• Произведение бесконечно малых — бесконечно малая.
• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 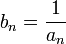— бесконечно большая последовательность.

Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.

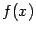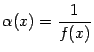Теорема 2.16 Пусть -- функция, бесконечно большая при базе . Тогда величина -- бесконечно малая при базе .

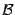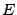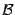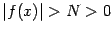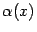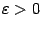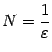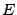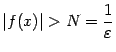Доказательство. Для начала заметим, что на всех достаточно далёких окончаниях базы будет , так что функция определена на этих окончаниях. Далее, пусть взято некоторое . Положим и выберем такое окончание , что при 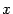из этого окончания. Тогда 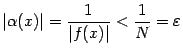при таких 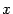, что и означает, что .

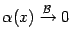Замечание 2.9 Утверждение, обратное к доказанной теореме, вообще говоря, неверно: если 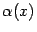-- бесконечно малая при базе 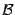, то функция 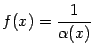не всегда является бесконечно большой при базе 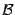, хотя бы потому, что может быть не определена ни на каком окончании 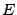базы 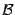. Простейший пример -- это постоянная величина 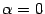, которая, очевидно, бесконечно мала при любой базе ( 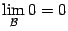), но 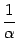не имеет смысла ни при каких 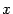. Однако если сделать дополнительное предположение, что 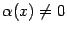при всех 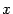из некоторого окончания 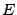базы 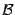, то обратное утверждение становится верным.

15.Второй замечательный предел, число е. Понятие о натуральных логарифмах.

Определение. Числом 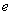(вторым замечательным пределом) называется предел числовой последовательности :

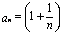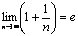, где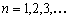

Прямым вычислением можно убедиться, что 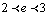, 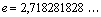(иррациональное число, число Эйлера).

Если рассмотреть функцию 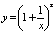, то при 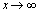функция имеет предел, равный числу :

.

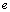Или если 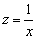, то .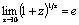

Непосредственное вычисление этого предела приводит к неопределенности 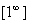. Однако доказано, что он равен числу 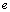. Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .

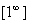Число 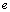(число Эйлера, неперово число) играет важную роль в математическом анализе. График функции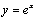

Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию 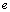, называемые натуральными. Натуральные логарифмы обозначаются символом .

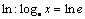Пример. .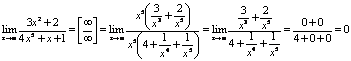

Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.

Функция f(x) называется непрерывной в точке х = а, если она определена в некоторой двусторонней окрестности этой точки, включая и саму эту точку.

Функция называется непрерывной на промежутке, если она непрерывна во всех точках этого промежутка.

Точки разрыва и их типы

Определение 2. Точка х = а называется точкой устранимого разрыва, если в этой точке функция имеет равные между собой конечные пределы, но сама в этой точке либо принимает другое значение, либо вообще не определена.

Определение 3. Точка х = а называется точкой разрыва первого рода, если в этой точке функция имеет конечные, но различные односторонние пределы. При этом разность

f(a + 0) - f(a - 0)

называется скачком функции в точке х = а.

Определение 4. Точка х = а называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или равен .

Теорема 1. Если функции f(x) и g(x) непрерывны в точке х = а, то функции f(x) ± g(x), f(x) • g(x), , где g(a) 0 также непрерывны в этой точке.

Теорема 2. Если функция f(x) непрерывна в точке х = а, а функция g(y) непрерывна в точке у = b, b = f(a), то сложная функция g(f(x)) непрерывна в точке х = а.

Теорема 3. Все элементарные функции непрерывны во всех точках, где они определены.

Таблица производных простейших элементарных функций

Легко получить следующую таблицу производных основных элементарных функций, используя определение производной. Для более подробного изучения данного материала рекомендуем использовать, например, "Математический анализ" ч.1 В.А. Ильина, В.А. Садовничего, Бл.Х. Сендова.

1. (u^a(x))' = a u^a-1(x)u'(x), в частности,

(1/u(x))' = -u'(x)/u2(x), ( )' = u'(x)/2 ;

2. (log_au(x))' = (u'(x)log_ae)/u(x) при 0<a¹1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x);

3. (a^u(x))' = a^u(x)ln a u'(x) при 0<a¹1, в частности, (e^u(x))' = u'(x)e^u(x);

4. (sin u(x))' = cos u(x)u'(x);

5. (cos u(x))' = -sin u(x)u'(x);

6. (tg u(x))' = u'(x)/cos²u(x) x¹ p/2+p n, n=0,+-1,...;

7. (ctg u(x))' = -u'(x)/sin²u(x) x¹ p n, n=0,+-1,...;

8. (arcsin u(x))' = u'(x)/ , -1<u(x)<1;

9. (arccos u(x))' = -u'(x)/ , -1<u(x)<1;

10. (arctg u(x))' = u'(x)/(1+u²(x));

11. (arcctg u(x))' = -u'(x)/(1+u²(x)).

Введем гиперболические функции:

sh x = (1/2)(e^x-e^-x)- гиперболический синус;

ch x = (1/2)(e^x+e^x)- гиперболический косинус;

th x = sh x/ch x -гиперболический тангенс;

cth x = ch x/sh x - гиперболический котангенс.

Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.

1. (sh x)' = ch x;

2. (ch x)' = sh x;

3. (th x)' = 1/ch² x;

4. (cth x)' = -1/sh² x.

Пример 7. Найти y', если

1. y(x) = x³arcsin x.

2. y(x) = ln sin (x²+1).

y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1)

Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.

"Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.
Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!

Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.

21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.

Теорема 1. (Теорема Ролля) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b);

3. на концах отрезка [a, b] принимает равные значения.

Тогда существует точка c О (a, b) такая, что f'(c) = 0.

Геометрическая интерпретация теоремы Ролля

Из теоремы Ролля следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна оси ОX (рис. 1).

Теорема 2. (Теорема Лагранжа) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с О (a, b) такая, что

f(b) − f(a) = f '(c) · (b − a) .

(1)

Формула (1) называется формулой Лагранжа, или формулой конечных приращений

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.

Геометрическая интерпретация теоремы Лагранжа

Представим формулу (1) в виде

f(b) − f(a) b − a = f '(c) .

(2)

Число

f(b) − f(a)

b − a

есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке
(c, f(c) ). Из формулы (2) следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

22. Достаточные признаки монотонности функции (график см. стр. 127 учебника)

y=f(x) называется монотонной (возраст. или убыв.) на промежутке М, если для любых двух значений,таких, что х2>x1

Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.

Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале

Исследование функций с помощью производных

Условия монотонности функции на интервале

Рассмотрим сначала достаточные условия строгой монотонности функции на интервале.

Теорема 22.1. Для того чтобы дифференцируемая на интервале (a;b) функция возрастала (убывала) на этом интервале достаточно, чтобы производная была положительной (отрицательной) всюду на этом интервале.

Доказательство. Рассмотрим случай, когда . Пусть x1 и x2 - любые две точки интервала (a;b), удовлетворяющие условию . На отрезке функция дифференцируема, а, следовательно, непрерывна. Поэтому к ней можно применить формулу Лагранжа:

, где .

По условию . Поэтому или , т.е. функция возрастает на интервале (a;b). Случай, когда , рассматривается аналогично.

Теорема доказана.

Из последней теоремы следует, что отличие от нуля производной является достаточным условием строгой монотонности функции. Однако это условие не является необходимым. Так, например, функция возрастает на любом интервале действительной оси, но при x=0 производная этой функции обращается в нуль (рис. 6). Следующая теорема устанавливает необходимое и достаточное условие монотонности функции.

воторой вариант : Достаточные признаки монотонности ф-ций (один из них доказать).

Теорема (достаточное условие возрастания ф-ции). Если производная дифференцируемой ф-ции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Рассм х₁ и х₂ на данном промежутке Х. Пусть х₂>х_1,х_1,х₂єХ. Докажем, что f(x₂)>f(x₁).Для ф-ции f(x) на отрехке [x₁;x₂] выполняются условия т. Лагранжа, поэтому f(x₂)-f(x₁)=f ^/(Е)(x₂-x₁), где х₁<Е>х_2, т е Е є промежутку, на кот производная положительна, следов. f^/(Е)>0 и правая часть равенства lim_{x→xo(x→∞)} f(x)/g(x)= lim_{x→xo(x→∞)} f^/(x)/g^/(x)- положительна. f(x₂)-f(x₁)>0 и f(x₂)>f(x₁).

Теорема (достаточное усл убывания ф-ции): Если производная дифференцируемой ф-ции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

23. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).

Общая схема исследования функций и построения их графиков. Пример.

1. область определения. Точки разрыва.

2. если есть точки разрыва, то находим ВА

3. исследуем поведение функций при x→∞, т.е. находим ГА

4. y’. y’=0, схема знаков производных между критическими точками, устанавливаем точки экстремума

5. точки пересечения гр.функций с осями 0х и 0у

6. исследование на четность/нечетность функции

Метод наименьших квадратов.

Дана экспериментальная зависимость

x	x1	x2	….	xn
y	y1	y2	….	yn

n-экспериментальных точек

Теорема.

Пусть функции и определены соответственно на промежутках и , причем . Если функция имеет на первообразную и, следовательно,

(1)

а функция дифференцируема на , то функция имеет на , первообразную и

(2)

Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде

то будет видно, что, для того чтобы вычислить интеграл ), можно сделать подстановку , вычислить интеграл и затем вернуться к переменной , положив .

Теорема 1. Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.

В таком случае

(22)

Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.

Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.

36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.

Неопределенный интеграл

Рассмотрим дифференцируемые функции переменной

U=U(x) и V=V(x)

Т.к. d(uv) = (uv)’dx=u’vdx+uv’dx= du*v+u*dv, то проинтегрируем по переменной х это равенство и учтем, что интеграл суммы функции – это сумма интегралов

⌠d(uv)= ⌠vdu+⌠udv

uv=⌠vdu+⌠udv

Метод интегрирования по частям применяется, когда нельзя вычесть интеграл методом замены переменной.

Пример.

⌠lnx*x⁸dx = {u=lnx;dv= x⁸dx; du = 1/8dx; v= ⌠ x⁸dx= x⁹/9}=lnx* x⁹/9-⌠ x⁹/9-1/xdv=lnx* x⁹/9-1/9⌠ x⁸dx=lnx* x⁹/9-1/9* x⁹/9+C

Определенный интеграл.

^b⌠udv=(uv-⌠vdu)^b│

^{a a}

u=u(x), v=v(x)

^b⌠udv=uv^b│-⌠ ^b vdu

^{a a a}

Формула Ньютона-Лейбница.

Определенный интеграл в пределах от a и b от непрерывной функции равен приращению любой ее первообразной на отрезке [a;b].

^b⌠f(x)dx = F(b)-F(a)

^a

1.при x=a ^a⌠f(t)dt=F(a)+C

^a

F(a)+C→C= -F(a)

2.x=b

^b⌠f(t)dt=F(b)-F(a)

^a

34. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).

Опр. Несобственным интегралом ^+∞∫_а f(x) dx от фун-и f(x) на полуинтервале [a;+∞] наз-ся предел фун-и Ф(t) при t, стремящимся к +∞.

^+∞∫_-∞ e^-x2/2 dx – несобственный интеграл Эйлера-Пуассона.

Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.

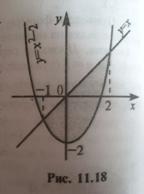
1.Пусть фун-я y=f(x) неотрицательна и непрерывна на отрезке [a,b]. Тогда по геометрич.смыслу определ.интеграла площадь S под кривой y=f(x) на [a,b] численно равна опред.интегралу, т.е. S = ^b∫_a f(x)dx. 2.Пусть фун-я y=f(x) неположительна и непрерывна на [a,b]. Тогда S = ^b∫_a (-f(x)) dx, т.е. S = - ^b∫_a f(x)dx. 3.Пусть на отрезке задана непрерывная фун-я общего вида. Тогда, S=S₁+S₂+S₃, т.е. равна алгебраич.сумме соответствующих опред.интегралов: S = ^c∫_a f(x)dx - ^d∫_c f(x)dx + ^b∫_d f(x)dx. 4.Тео-ма. Пусть на отрезке заданы непрерывные фун-и y=f₁(x) и y=f₂(x) такие, что f₂(x)> f₁(x). Тогда площадь S фигуры, заключенной между кривыми y=f₂(x) и y=f₁(x), на отрезке вычисляется по формуле: S = ^b∫_a (f₂(x) – f₁(x)) dx. При-р:Найти пло-дь фиг-ры, огранич.линиями y=x²-2, y=x.(рис.11.18).Реш-е: система: y=x²-2 и y=x => (-1;-1) и (2;2). На отр-ке [-1,2] x>x²-2. f₂(x)=x, f₁(x)=x²-2. S=²∫_-1 (x-(x²-2)) dx = x²/2 ²|_-1 – x³/3 ²|_-1 +2x ²|_-1 =1/2(4-(-1)²) – 1/3(2³-(-1)³) +2(2-1)) = 4,5 (ед.²).

Чётность

Основная статья: Нечётные и чётные функции

• Функция 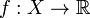называется нечётной, если справедливо равенство

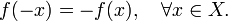
• Функция f называется чётной, если справедливо равенство

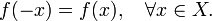
Ограниченность функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что

m ≤ f(x) ≤ M

при хє(a,b).

Число m_o= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,

а число M_o= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).

Разность M_o- m_o называется колебанием функции на промежутке (a,b).

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

9. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая).

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

• алгебраические:
• степенная;
• рациональная.
• трансцендентные:
• показательная и логарифмическая;
• тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Постоянная функция.

Постоянной называется функция, заданная формулой у = b, где b - некоторое число.

Графиком постоянной функции у = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рисунке изображены графики нескольких постоянных функций. В частности, графиком функции y = 0 является ось абсцисс.

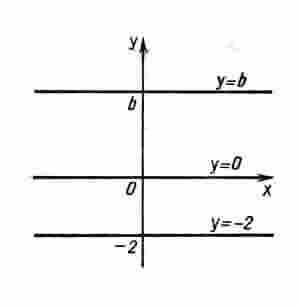
Если b = 0, то получаем прямую пропорциональность у = kх.

Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

Показательная функция — математическая функция 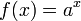, где a называется «основанием», а x — «показателем» степени.

• В вещественном случае основание степени 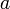— некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.
• В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
• В самом общем виде — u^v, введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

Функцияy=log_a х(гдеа> 0,а$$\ne$$1) называется логарифмической.

Построение графиков. График логарифмической функции log_aх можно построить, воспользовавшись тем, что функция log_aх обратна показательной функции y = a^x. Поэтому достаточно построить график функции y = a^x, а затем отобразить его симметртрично относительно прямой у = х.

Свойства функции у = logaх , a > 1: 1. D(f) = (0; +$$\infty$$); 2. не является ни четной, ни нечетной; 3. возрастает на (0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. не имеет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-$$\infty$$;+ $$\infty$$); 8. выпукла вверх; дифференцируема.	Свойства функцииу= logaх, 0 <a< 1 : 1. D(f) = (0;+$$\infty$$ ); 2. не является ни четной, ни нечетной; 3. убывает на (0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. нет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-;$$\infty$$+ $$\infty$$); 8. выпукла вниз; дифференцируема.
Свойства функции у = ln х : 1. D(f) = (0; +$$\infty$$); 2. не является ни четной, ни нечетной; 3. возрастает на {0; +$$\infty$$); 4. не ограничена сверху, не ограничена снизу; 5. не имеет ни наибольшего, ни наименьшего значений; 6. непрерывна; 7. E(f) = (-$$\infty$$;+ $$\infty$$); 8. выпукла вверх; дифференцируема.

10. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести).

Определение. Уравнением линии (кривой) на плоскости называется уравнение, 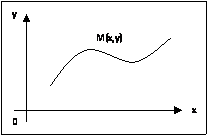которому удовлетворяют координаты 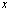и 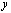каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Если точка 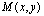передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты 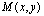называются текущими координатами.

Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию. Например: 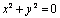определяет только одну точку (0;0); 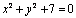не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю. Чтобы убедится, лежит ли точка 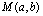на данной линии