Шаг 3. Определение проекций начальной скорости и ускорения.

Шаг 4. Построение графика зависимости проекции скорости автомобиля от времени и определения по этому графику искомых величин t и L.

Ответ: t = _____________ L = ___________________

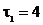4. Пассажир, стоящий на платформе, заметил, что первый вагон прибывающего поезда прошёл мимо него за время с, а второй вагон — за 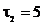с. Когда поезд остановился, пассажир оказался на расстоянии 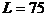м от начала первого вагона. Определите модуль ускорения поезда, считая его постоянным.

5. Вдоль наклонной плоскости скользит брусок. Участок АВ брусок проходит, двигаясь равноускоренно, со средней скоростью, модуль которой равен υ₀. В точке А его скорость по модулю на Δυ меньше, чем в точке В. Определите скорость бруска в точке С, расположенной между точками А и В и отстоящей от точки А на 1/n часть длины участка АВ.

6. Ракета, запускаемая вертикально вверх с поверхности Земли, в течение 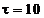сразгоняется с ускорением, модуль которого в 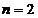раза больше модуля ускорения свободного падения g. Затем двигатели прекращают работу. Определите: а) модуль максимальной скорости ракеты; б) высоту подъёма ракеты; в) путь, пройденный ракетой. Считайте движение ракеты с неработающими двигателями свободным падением.

7. Кабина лифта движется вертикально вверх с постоянной скоростью относительно Земли. На пол кабины вертикально вниз падает упругий шарик. Известно, что после отскока шарик, не касаясь потолка, удаляется от пола лифта на максимальное расстояние за время τ, а к моменту следующего удара о пол проходит путь S относительно Земли. Определите скорость лифта.

8. Зачеркните в пунктах а) и б) варианты, образующие неверные утверждения.

При свободном падении точечного тела, брошенного под углом к горизонту:

а) проекция его скорости на лежащую в плоскости падения горизонтальную ось X, неподвижную относительно Земли:

не изменяется с течением времени; всё время увеличивается; всё время уменьшается; до некоторого момента уменьшается, а потом увеличивается; до некоторого момента увеличивается, а потом уменьшается.

б) проекция его скорости на неподвижную относительно Земли и направленную вертикально вверх ось Y:

не изменяется с течением времени; увеличивается с течением времени; уменьшается с течением времени; до некоторого момента уменьшается, а потом увеличивается; до некоторого момента увеличивается, а потом уменьшается.

9. Из миномёта произведён выстрел по мишени, находящейся на высоте h над горизонтальной поверхностью. Мина вылетает под углом α к горизонту с начальной скоростью, модуль которой равен v₀. После пролёта максимальной высоты мина попадает в мишень. Пренебрегая влиянием воздуха на мину, определите время t_п и дальность L её полёта по горизонтали от места выстрела до места попадания в мишень, модуль скорости υ(t_п) падения мины, а также высоту Н её максимального подъёма. Задачу решите аналитически.

Решение.

Шаг 0.

Будем считать мину ___________ телом, а её движение _______________ падением, поскольку влиянием воздуха можно пренебречь. Поэтому в любой момент времени ускорение мины направлено ______________ и по модулю равно _______.

Шаг 1.

Систему отсчёта свяжем с ___________. Начало отсчёта поместим в точку выстрела. Ось X направим горизонтально в направлении ______________. Ось Y направим _________________. Часы включим в момент ____________.

Шаг 2.

В выбранной системе отсчёта начальные координаты мины: х 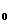= _____, y = _______.

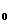Шаг 3.

Проекции начальной скорости 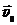мины на координатные оси X и Y соответственно равны: 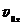= ____________________________________________и = ______________________________________.

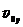Шаг 4.

Ускорение 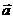мины в любой момент времени равно ___ и направлено ______________________ оси Y. Поэтому проекции ускорения мины на оси X и Y равны: 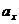= ___; 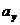= _____. Движение мины вдоль оси X является _________________, а ее координата х изменяется по закону: x(t) = _______________________.

Так как проекция ускорения мины на ось Y _______________, координата мины вдоль оси Y изменяется по закону: y(t) = ________________________.

Шаг 4*.

Законы изменения проекций скорости мины от времени имеет вид:

υ_х (t) = ______________________, υ_y (t) = ______________________.

Шаг 5.

По условию задачи в момент времени t_п падения мины на мишень координата у мины удовлетворяет уравнению: y(t_п) = _____________________.

В этот момент проекция скорости мины на ось y равна:

υ_y(t_п) = ________________________.

Время t_м достижения максимальной высоты полёта определим из условия равенства нулю компоненты скорости мины вдоль оси ____: ___________________________________.

Шаг 6.

Система уравнений имеет вид:

y(t) = ________________________; (1) (закон движения по оси Y)

x(t) = ________________________; (2) (закон движения по оси X)

υ_y(t) = _______________________; (3) (закон изменения проекции скорости

вдоль оси Y)

υ_x(t) = _______________________; (4) (закон изменения проекции скорости

вдоль оси X)

y(t_п) = _______________________; (5) (условие падения)

υ_y (t_м) = ______________________; (6) (условие максимального подъёма)

Шаг 7. Решение системы уравнений.

Из уравнений (1) и (5) получим уравнение для расчета времени движения до попадания в мишень: _________________________________________.

Решение этого уравнения даёт два корня, отвечающие моментам времени прохождения миной уровня h. Попаданию в мишень соответствует больший из этих корней. Поэтому: t_п = _____________________.

Подставляя это значение в уравнение (2), вычисляем дальность полёта мины по горизонтали (вдоль оси Х): L = _______________________________.

Подстановка полученного значения времени полёта t_п мины в уравнение (3) позволяет вычислить проекцию скорости мины v_y(t_п) на ось Y в момент попадания в мишень: υ_y(t_п) = _______________________________.

Модуль скорости мины в момент попадания в мишень определим из (3) и (4): υ(t_п) = __________________________.

Угол φ между вектором скорости мины в момент t_п и осью Х определим из соотношения: tgφ = _____________.

Из уравнений (7) и (3) найдём время подъёма мины на максимальную высоту:

t_м = _____________________; а затем из (1), определим максимальную высоту подъёма мины: H = _____________________________________.

Ответ: Время полёта мины t_п = _____________; в момент t_п модуль скорости мины υ(t_п) = _____________. Вектор скорости мины в этот момент образует с осью Х угол φ = _____.

Дальность полёта мины по горизонтали L = ___________, а максимальная высота подъёма мины H = _________.

10. Камень, брошенный вертикально вверх, упал на Землю через t с. На каком расстоянии по горизонтали от точки бросания упадёт камень на Землю, если его бросить с той же начальной скоростью, но под углом a к горизонту?

11. Самолёт, летящий на высоте Н горизонтально со скоростью 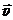, сбрасывает груз. Под каким углом к горизонту штурман должен видеть место приземления груза в оптический прицел в момент сброса, чтобы обеспечить попадание?