I. признаки возрастания и убывания функции
Критерий возрастания и убывания функции: пусть 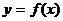 - дифференцируемая на интервале
- дифференцируемая на интервале 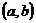 функция. Функция
функция. Функция 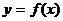 возрастает на
возрастает на 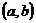 тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
Функция 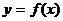 убывает на
убывает на 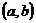 тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
Критерий возрастания и убывания функции удобно представляется в виде схемы:
| f(x)ä | 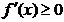 |
| f(x) æ | 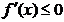 |
- Достаточные условия существования экстремума
Критическими точками функции (первого рода) называются точки, в которых производная функции равна нулю или не существует. По теореме Ферма (необходимое условие существования экстремума функции), точки экстремума нужно искать среди критических точек. Но не любая критическая точка является точкой экстремума функции. Чтобы выяснить, в каких критических точках функция имеет экстремум, рассмотрим достаточные условия существования экстремума.
Достаточные условия существования экстремума (критерий нахождения точек экстремума):пусть функция 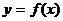 непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда:
непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда:
1. если производная 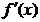 при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
2. если производная 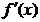 при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума.
при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума.
Критерий нахождения точек экстремума функции удобно представляется в виде схемы:
| хо – критическая точка: f`(xо)=0 или f`(xо) не существует | ||||
| хо – точка минимума |   хо хо | 
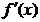  | ||
| хо – точка максимума | 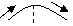 хо хо |
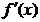  |
Для нахождения промежутков монотонности и экстремумов функции используется следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции.
3. Определите критические точки первого рода (f'(xo)=0 или f'(xo) не существует).
4. На числовой оси отметьте критические точки и определите знаки производной на каждом из получившихся интервалов.
5. Найдите интервалы монотонности, выпишите точки экстремума функции (если они есть), используя соответствующие критерии, вычислите значения функции в точках экстремума.
Пример 1. Найдите промежутки монотонности и экстремумы функции 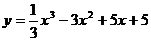 .
.
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции: 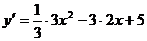 =
= 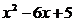 .
.
3. Определим критические точки первого рода (у'=0): 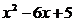 =0;
=0;
х1=1 или х2=5.
4. На числовой оси отметим критические точки х1=1 и х2=5. Эти точки разбивают область определения функции на три интервала (-∞;1), (1;5); (5;+∞). Расставим знаки производной функции у' = 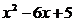 на каждом из полученных интервалов:
на каждом из полученных интервалов:
при х=0  (-∞;1) у'(0)=5>0;
(-∞;1) у'(0)=5>0;
при х=2  (1;5) у'(2)=
(1;5) у'(2)= 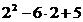 =-3<0;
=-3<0;
при х=6  (5;+∞) у'(6)=
(5;+∞) у'(6)= 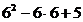 =5>0.
=5>0.
|
|
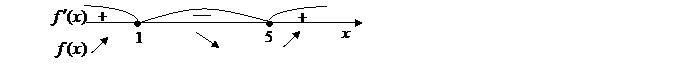
5. Согласно критерию возрастания и убывания функция 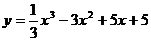 возрастает при х
возрастает при х  (-∞;1]
(-∞;1]  [5;+∞), убывает при х
[5;+∞), убывает при х  [1;5].
[1;5].
Согласно критерию нахождения точек экстремума х=1 – точка максимума, х=5 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках: 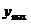 =
= 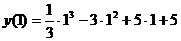 =
= 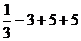 =
= 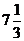 - максимум функции;
- максимум функции;
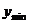 =
= 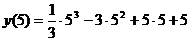 =
= 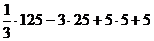 =
= 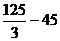 =
= 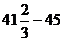 =
= 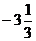 - минимум функции.
- минимум функции.
Ответ: 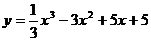 возрастает при х
возрастает при х  (-∞;1]
(-∞;1] 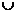 [5;+∞), убывает при х
[5;+∞), убывает при х 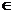 [1;5];
[1;5];
х=1 – точка максимума; 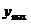 =
= 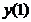 =
= 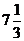 ;
;
х=5 – точка минимума; 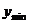 =
= 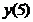 =
= 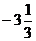 .
.
Пример 2. Найдите промежутки монотонности и экстремумы функции 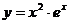 .
.
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции по правилу производной произведения:
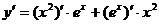 =
= 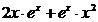 =
= 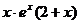
3. Определим критические точки первого рода (у' =0): 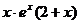 =0;
=0;
х1=0 или 2+х=0 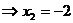
 (ех≠0 для всех х из множества R).
(ех≠0 для всех х из множества R).
4. На числовой оси отметим критические точки х=-2 и х=0. Эти точки разбивают область определения функции на три интервала (-∞;-2), (-2;0); (0;+∞). Расставим знаки производной функции у'= 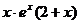 на каждом из полученных интервалов:
на каждом из полученных интервалов:
|
|
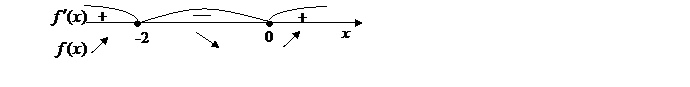
5. Согласно критерию возрастания и убывания функция 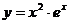 возрастает при
возрастает при
х 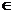 (-∞;-2]
(-∞;-2] 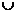 [0;+∞), убывает при х
[0;+∞), убывает при х 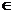 [-2;0].
[-2;0].
Согласно критерию нахождения точек экстремума х=-2 – точка максимума, х=0 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках: 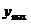 =
= 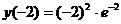
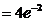 =
= 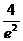 - максимум функции;
- максимум функции;
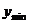 =
= 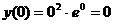 - минимум функции.
- минимум функции.
Ответ: 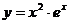 возрастает при х
возрастает при х 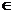 (-∞;-2]
(-∞;-2] 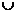 [0;+∞), убывает при х
[0;+∞), убывает при х  [-2;0];
[-2;0];
х=-2 – точка максимума; 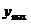 =
= 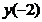 =
= 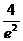 ;
;
х=5 – точка минимума; 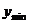 =
= 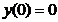 .
.
Список литературы:
1. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 38-39, стр. 220-226.
2. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с. – Глава 6, §6.3, стр. 126 – 127; §6.7, стр. 138 – 141.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §7, стр. 255– 265.
