И алгебраических дополнений – 1 ч.
Цель:формирование умения находить определители второго, третьего и четвертого порядка, вычислять миноры и алгебраические дополнения элементов определителя.
Задание для самостоятельной внеаудиторной работы:
&3.1. Запомните, какова методика нахождения определителей второго, третьего и четвертого порядка. Выучите, что называют минорами и алгебраическими дополнениями элементов определителя.
?3.2.Вычислите определитель:
а)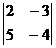 ;б)
;б)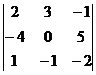 ;в)
;в) 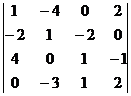 .
.
&3.3. Выучите, какими основными свойствами обладает определитель.
?3.4. Вычислите определитель 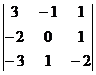 . Используя свойства определителей, найдите определитель:
. Используя свойства определителей, найдите определитель:
а) 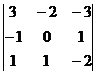 ; б)
; б) 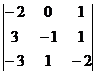 ; в)
; в) 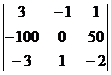 ; г)
; г) 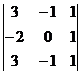 .
.
?3.5. Найдите миноры и алгебраические дополнения элементов второй строки определителя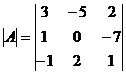 .
.
¶3.6.Вычислите определитель:  а)
а)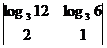 ;б)
;б)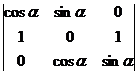 .
.
¶3.7. Решите уравнение и неравенство: а) 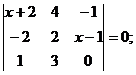 б)
б) 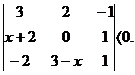
Методические указания по выполнению работы:
Каждой квадратнойматрице можно поставить в соответствиенекоторое число |A|, называемое её определителем, следующим образом:
1. Второго порядка: 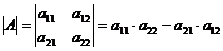 .
.
2. Третьего порядка:
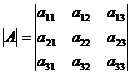 =
= 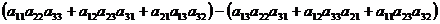 .
.
3. Любого порядка. Определитель равен сумме произведенийэлементов любой строки или столбца определителя на их алгебраические дополнения:
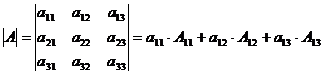 =
= 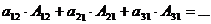
где Аij - алгебраическое дополнениеэлемента аij : Аij = (-1)i+ j ·Мij;
Мij – минорэлемента аij - новый определитель порядка (п-1), полученный из 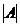 вычеркиваниемi-й строки и j-го столбца, на пересечении которых находится элемент аij.
вычеркиваниемi-й строки и j-го столбца, на пересечении которых находится элемент аij.
Свойства определителей:
1. Определитель не изменится, если его строки заменить столбцами и наоборот (свойство равноправности строк и столбцов).
2. При перестановке двух строк или столбцов определитель меняет свой знак на противоположный.
3. Определитель с двумя одинаковыми строками или столбцами равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
Следствие: Если элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.
Приведем примеры нахождения определителей второго, третьего и четвертого порядков:
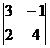
Пример 1. Найдите определитель |A| =
Решение: 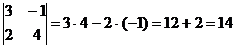 .
.
Ответ: |A| = 14.
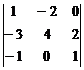
Пример 2. Найдите определитель матрицы А =
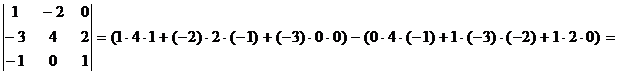 Решение:
Решение:
= 4 + 4 + 0 – 6 = 2. Ответ: |A| = 2.
Для нахождения определителя четвертого порядка необходимо уметь вычислять миноры и алгебраические дополнения элементов определителя.
Пример 3.Найдите миноры и алгебраические дополнения элементов третьего столбца определителя 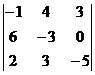 .
.
Решение:
1. Минор элемента а13 (М13) получаем вычеркиванием из определителя первой строки и третьего столбца:
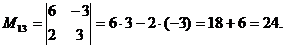
2. Алгебраическое дополнение элемента а13 (А13)найдем по формуле: А13=(-1)1+3М13;
А13=(-1)4∙24=24.
3. М23получаем вычеркиванием из определителя второй строки и третьего столбца:
М23= 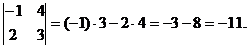
4. А23 найдем по формуле: А23=(-1)2+3М23;
А23 = (-1)5∙(-11) = 11.
5. М33получаем вычеркиванием из определителя третьей строки и третьего столбца:
М33= 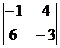 = (-1)∙(-3) - 6∙4 = 3 - 24 = -21.
= (-1)∙(-3) - 6∙4 = 3 - 24 = -21.
6. А33 найдем по формуле: А33=(-1)3+3М33;
А33 = (-1)6∙(-21) = -21.
Ответ:М13=24, А13=24; М23= -11, А23=11; М33= -21, А33= -21.
Пример 4. Вычислите определитель четвертого порядка: 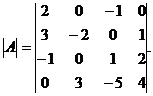
Решение:
1. Разложим определитель по элементам первой строки: 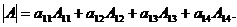
Так как а11=2, а12=0, а13= -1, а14=0, то 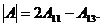
2. Вычислим алгебраическое дополнение А11:
А11=(-1)1+1М11, где М11= 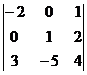 =(-2)∙1∙4+3∙0∙2+1∙0∙(-5) - (3∙1∙1+(-2)∙2∙(-5)+4∙0∙0 =
=(-2)∙1∙4+3∙0∙2+1∙0∙(-5) - (3∙1∙1+(-2)∙2∙(-5)+4∙0∙0 =
= -8+0+0-(3+20+0) = -8-23= -31.
Тогда А11=(-1)2∙(-31)= -31.
3. Вычислим алгебраическое дополнение А13:
А13=(-1)1+3М13, где М13= 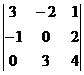 = 3∙0∙4+(-1)∙3∙1+0∙2∙(-2) - (1∙0∙0+4∙(-1)∙(-2)+3∙2∙3) =
= 3∙0∙4+(-1)∙3∙1+0∙2∙(-2) - (1∙0∙0+4∙(-1)∙(-2)+3∙2∙3) =
=0-3+0-(0+8+18) = -3-26 = -29.
Тогда А13=(-1)4∙ (-29) = -29.
4. Поскольку 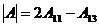 , получим:
, получим: 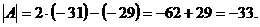
Ответ: 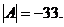
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с. – Глава 2, §2.2, стр. 17 – 33.
2. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 1, § 2, стр. 71 – 78.
