Числовые характеристики системы двух случайных величин
Среди числовых характеристик двумерной случайной величины важнейшими являются условное математическое ожидание и ковариация.
Условным математическим ожиданием дискретной случайной величины Y при X = х называют сумму произведений возможных значений Y на их условные вероятности
M(Y /X = x) = 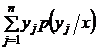 .
.
Для непрерывных случайных величин условное математическое ожидание определяется интегралом:
M(Y /X = x) = 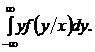
Условное математическое ожидание M(Y/ X = х) называется также регрессией величины Y на X.
Аналогично определяется регрессия X на Y:
-для дискретной случайной величины:
М(Х /Y = y) = 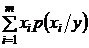 ;
;
-для непрерывной случайной величины:
M(X/Y = y) = 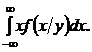
Ковариацией или корреляционным моментом случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
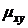 = М((Х – Mx)(Y – Му)).
= М((Х – Mx)(Y – Му)).
Коэффициентом корреляции rxy случайных величин X и Y называется отношение ковариации к произведению средних квадратичных отклонений этих величин:
rxy = 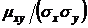 –1
–1 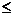 rху
rху 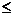 1.
1.
Линейной средней квадратической регрессией Y на X называется функция вида:
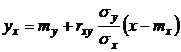 ,
,
где mx = М(Х), my = M(Y),
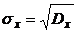 ,
, 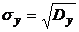 ,
, 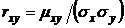 .
.
4.2. Найти регрессию величины Y на X для двух значений x1 = 3 и х2 = 6 на основе заданной таблицы распределения двумерной случайной величины
| X Y | ||
| 0,25 | 0,10 | |
| 0,15 | 0,05 | |
| 0,32 | 0,13 |
Решение. Условное математическое ожидание, или регрессия, величины Y на X находится на основе соотношения
M(Y /Х = xi) = 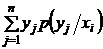 .
.
Определяем Р(Х = 3) и Р(Х = 6):
Р(Х = 3) = 0,25 + 0,15 + 0,32 = 0,72;
Р(Х = 6) = 0,10 + 0,05 + 0,13 = 0,28.
Вычисляем условные вероятности:
Р(Y = 10 / Х = 3) = 0,25/0,72 = 0,35; P(Y = 10 / Х = 6) = 0,10/0,28 = 0,36;
P(Y = 14 / Х = 3) = 0,15/0,72 = 0,21; P(Y = 14 / X = 6) = 0,05/0,28 = 0,18;
Р(Y = 18 / Х= 3) = 0,32/0,72 = 0,44; Р(Y = 18 / Х= 6) = 0,13/0,28 = 0,46.
Находим условные математические ожидания:
M(Y / X = 3) = 10 · 0,35 + 14 · 0,21 + 18 · 0,44 = 14,4;
M(Y / X = 6) = 10 · 0,36 + 14 · 0,18 + 18 · 0,46 = 14,3.
4.3. Задан закон распределения двумерной случайной величины (X, Y)
| Y X | |||
| 0,10 | 0,20 | 0,15 | |
| 0,05 | 0,14 | 0,11 | |
| 0,12 | 0,08 | 0,05 |
Найти условное математическое ожидание величины X для всех возможных значений величины Y.
4.4. Для заданного в задаче 4.3 закона распределения найти коэффициент корреляции между величинами X и Y.
Решение. Находим вероятности значений X = 1, X = 3, X = 4:
Р(Х = 1) = 0,10 + 0,20 + 0,15 = 0,45;
Р(Х = 3) = 0,05 + 0,14 + 0,11 = 0,30;
Р(Х = 4) = 0,12 + 0,08 + 0,05 = 0,25.
Определяем вероятности значений Y = 2, Y = 3, Y = 5:
P(Y = 2) = 0,10 + 0,05 + 0,12 = 0,27;
P(Y = 3) = 0,20 + 0,14 + 0,08 = 0,42;
P(Y = 5) = 0,15 + 0,11 + 0,05 = 0,31.
Находим M(Y):
M(Y) = 2 · 0,27 + 3 · 0,42 + 5 · 0,31 = 3,35.
Определяем М(Х):
М(Х) = 1 · 0,45 + 3 · 0,3 + 4 · 0,25 = 2,35.
Вычисляем М(Х2) и M(Y2):
М(Х2) = 1 · 0,45 + 9 · 0,3 + 16 · 0,25 = 7,15;
М(Y2) = 4 · 0,27 + 9 · 0,42 + 25 · 0,31 = 12,61.
Находим Dx, Dy:
Dx = 7,15 – 2,352 = 7,15 – 5,52 = 1,63;
Dy = 12,61 – 3,352 = 12,61 – 11,22 = 1,39.
Откуда 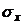 = 1,28;
= 1,28; 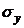 = 1,18.
= 1,18.
Ковариация величин X и Y может быть найдена по формуле
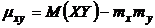 .
.
Итак,
M(XY) = 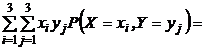
= 1 · 2 · 0,1 + 1 · 3 · 0,2 + 1 · 5 · 0,15 + 3 · 2 · 0,05 + 3 · 3 · 0,14 + 3 · 5 · 0,11 +
+ 4 · 2 · 0,12 + 4 · 3 · 0,08 +4 · 5 · 0,05 = 7,68,
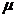 xy= 7,68 – 2,35 · 3,35 = – 0,19,
xy= 7,68 – 2,35 · 3,35 = – 0,19,
rxy = 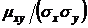 = – 0,19/(1,28 · 1,18) = – 0,126.
= – 0,19/(1,28 · 1,18) = – 0,126.
ПРАКТИКУМ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Задания
1. В партии из N изделий n изделий имеют скрытый дефект (табл. 2). Какова вероятность того, что из взятых наугад т изделий k изделий являются дефектными?
2. В магазине выставлены для продажи n изделий, среди которых k изделий некачественные (табл. 3). Какова вероятность того, что взятые случайным образом m изделий будут некачественными?
3. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n1 с первого завода, n2 со второго, n3 с третьего (табл. 4). Вероятность качественного изготовления изделий на первом заводе p1, на втором р2, на третьем р3. Какова вероятность того, что взятое случайным образом изделие будет качественным?
4. Дано распределение дискретной случайной величины X (табл. 5). Найти математическое ожидание и среднее квадратичное отклонение.
5. В городе имеется N оптовых баз (табл. 6). Вероятность того, что требуемого сорта товар отсутствует на этих базах одинакова и равна р. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
6. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно Мх, среднее квадратичное отклонение равно 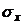 (табл. 7). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (а, b).
(табл. 7). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (а, b).
7. Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины (табл. 8).
Таблица 2
| Вариант | N | n | m | k | Вариант | N | n | m | k |
Таблица 3
| Вариант | n | k | m | Вариант | n | k | m |
Таблица 4
| Вариант | n1 | p1 | n2 | p2 | n3 | p3 | Вариант | n1 | p1 | n2 | p2 | n3 | p3 |
| 0,9 | 0,8 | 0,7 | 0,9 | 0,8 | 0,7 | ||||||||
| 0,8 | 0,7 | 0,7 | 0,8 | 0,7 | 0,9 | ||||||||
| 0,9 | 0,7 | 0,9 | 0,9 | 0,8 | 0,8 | ||||||||
| 0,7 | 0,9 | 0,8 | 0,8 | 0,6 | 0,7 | ||||||||
| 0,9 | 0,8 | 0,6 | 0,9 | 0,8 | 0,7 | ||||||||
| 0,8 | 0,8 | 0,9 | 0,9 | 0,7 | 0,8 | ||||||||
| 0,8 | 0,9 | 0,8 | 0,9 | 0,8 | 0,9 | ||||||||
| 0,7 | 0,8 | 0,9 | 0,9 | 0,7 | 0,7 | ||||||||
| 0,9 | 0,8 | 0,9 | 0,8 | 0,9 | 0,8 | ||||||||
| 0,8 | 0,7 | 0,8 | 0,8 | 0.8 | 0,9 | ||||||||
| 0,9 | 0,9 | 0,8 | 0,9 | 0,8 | 0,6 | ||||||||
| 0,8 | 0,9 | 0,8 | 0,8 | 0,7 | 0,8 | ||||||||
| 0,8 | 0,9 | 0,7 | 0,8 | 0,9 | 0,8 | ||||||||
| 0,9 | 0,7 | 0,7 | 0,9 | 0,8 | 0,9 | ||||||||
| 0,8 | 0,9 | 0,9 | 0,7 | 0,9 | 0,7 |
Таблица 5
| Вариант | Числовые данные | Вариант | Числовые данные | ||||||||
| xi | -5 | xi | |||||||||
| pi | 0,4 | 0,3 | 0,1 | 0,2 | pi | 0,4 | 0,3 | 0,3 | |||
| xi | 0,2 | 0,5 | 0,6 | 0,8 | xi | ||||||
| pi | 0,1 | 0,5 | 0,2 | 0,2 | pi | 0,3 | 0,1 | 0,1 | 0,5 | ||
| xi | -6 | -2 | xi | ||||||||
| pi | 0,1 | 0,3 | 0,4 | 0,2 | pi | 0,3 | 0,2 | 0,1 | 0,4 | ||
| xi | 0,2 | 0,5 | 0,6 | xi | |||||||
| pi | 0,5 | 0,4 | 0,5 | 0,1 | pi | 0,4 | 0,2 | 0,1 | 0,3 | ||
| xi | -8 | -2 | xi | ||||||||
| pi | 0,1 | 0,3 | 0,4 | 0,2 | pi | 0,2 | 0,4 | 0,4 | |||
| xi | -2 | xi | |||||||||
| pi | 0,1 | 0,3 | 0,4 | 0,2 | pi | 0,4 | 0,3 | 0,1 | 0,2 | ||
| xi | -3 | xi | |||||||||
| pi | 0,3 | 0,4 | 0,1 | 0,2 | pi | 0,1 | 0,5 | 0,2 | 0,2 | ||
| xi | xi | ||||||||||
| pi | 0,1 | 0,4 | 0,5 | pi | 0,3 | 0,1 | 0,4 | 0,2 | |||
| xi | -4 | -1 | xi | ||||||||
| pi | 0,3 | 0,1 | 0,4 | 0,2 | pi | 0,1 | 0,4 | 0,5 |
Окончание табл. 5
| xi | -3 | xi | -3 | -1 | |||||||
| pi | 0,3 | 0,4 | 0,1 | 0,2 | pi | 0,4 | 0,3 | 0,1 | 0,2 | ||
| xi | -6 | -2 | xi | ||||||||
| pi | 0,2 | 0,4 | 0,1 | 0,3 | pi | 0,1 | 0,3 | 0,3 | 0,3 | ||
| xi | xi | ||||||||||
| pi | 0,5 | 0,1 | 0,4 | pi | 0,5 | 0,1 | 0,3 | 0,1 | |||
| xi | -5 | -3 | xi | ||||||||
| pi | 0,2 | 0,1 | 0,1 | 0,6 | pi | 0,2 | 0,1 | 0,7 | |||
| xi | xi | ||||||||||
| pi | 0,2 | 0,2 | 0,4 | 0,2 | pi | 0,3 | 0,2 | 0,4 | 0,1 | ||
| xi | xi | ||||||||||
| pi | 0,3 | 0,1 | 0,3 | 0,3 | pi | 0,2 | 0,3 | 0,1 | 0,4 |
Таблица 6
| Вариант | N | Р | Вариант | N | Р |
| 0,2 | 0,15 | ||||
| 0,25 | 0,24 | ||||
| 0,1 | 0,1 | ||||
| 0,2 | 0,12 | ||||
| 0,1 | 0,14 | ||||
| 0,2 | 0,16 | ||||
| 0,3 | 0,15 | ||||
| 0,1 | 0,13 | ||||
| 0,12 | 0,21 | ||||
| 0,3 | 0,16 | ||||
| 0,15 | 0,19 | ||||
| 0,18 | 0,26 | ||||
| 0,24 | 0,14 | ||||
| 0,14 | 0,15 | ||||
| 0,16 | 0,22 |
Таблица 7
| Вариант | Мх | 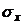 | а | b | Вариант | Мх | 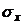 | а | b |
Окончание табл. 7
Таблица 8
| Вариант | Числовые данные | Вариант | Числовые данные | ||||||
| Y X | X Y | ||||||||
| 0,16 | 0,10 | 0,28 | 0,14 | 0,15 | 0,21 | ||||
| 0,14 | 0,20 | 0,12 | 0,16 | 0,20 | 0,14 | ||||
| Y X | X Y | ||||||||
| 0,06 | 0,18 | 0,24 | 0,14 | 0,12 | 0,13 | ||||
| 0,12 | 0,13 | 0,27 | 0,13 | 0,20 | 0,28 | ||||
| Y X | X Y | ||||||||
| 0,12 | 0,24 | 0,22 | 0,11 | 0,13 | 0,26 | ||||
| 0,20 | 0,15 | 0,07 | 0,21 | 0,06 | 0,23 | ||||
| Y X | X Y | ||||||||
| 0,16 | 0,10 | 0,28 | 0,22 | 0,09 | 0,32 | ||||
| 0,14 | 0,20 | 0,12 | 0,14 | 0,17 | 0,06 | ||||
| Y X | X Y | ||||||||
| 0,06 | 0,18 | 0,24 | 0,14 | 0,11 | 0,18 | ||||
| 0,12 | 0,13 | 0,27 | 0,23 | 0,04 | 0,30 | ||||
| Y X | X Y | ||||||||
| 0,16 | 0,10 | 0,28 | 0,21 | 0,07 | 0,23 | ||||
| 0,14 | 0,20 | 0,12 | 0,11 | 0,20 | 0,18 | ||||
| Y X | X Y | ||||||||
| 0,12 | 0,13 | 0,24 | 0,15 | 0,23 | 0,15 | ||||
| 0,18 | 0,06 | 0,27 | 0,21 | 0,09 | 0,17 |
Окончание табл. 8
| Y X | Х Y | ||||||||
| 0,06 | 0,18 | 0,24 | 0,13 | 0,14 | 0,19 | ||||
| 0,12 | 0,13 | 0,27 | 0,24 | 0,08 | 0,22 | ||||
| Y X | Х Y | ||||||||
| 0,12 | 0,13 | 0,24 | 0,23 | 0,07 | 0,15 | ||||
| 0,18 | 0,06 | 0,27 | 0,17 | 0,20 | 0,18 | ||||
| Y X | X Y | ||||||||
| 0,13 | 0,24 | 0,12 | 0,11 | 0,21 | 0,14 | ||||
| 0,18 | 0,06 | 0,27 | 0,20 | 0,09 | 0,25 | ||||
| Х Y | X Y | ||||||||
| 0,13 | 0,24 | 0,12 | 0,30 | 0,12 | 0,10 | ||||
| 0,18 | 0,06 | 0,27 | 0,08 | 0,12 | 0,28 | ||||
| X Y | X Y | ||||||||
| 0,12 | 0,24 | 0,22 | 0,21 | 0,18 | 0,14 | ||||
| 0,20 | 0,15 | 0,07 | 0,08 | 0,14 | 0,25 | ||||
| X Y | X Y | ||||||||
| 0,13 | 0,08 | 0,12 | 0,09 | 0,15 | 0,16 | ||||
| 0,20 | 0,16 | 0,31 | 0,17 | 0,23 | 0,20 | ||||
| X Y | X Y | ||||||||
| 0,30 | 0,20 | 0,10 | 0,11 | 0,24 | 0,17 | ||||
| 0,05 | 0,12 | 0,23 | 0,21 | 0,08 | 0,19 | ||||
| X Y | X Y | ||||||||
| 0,24 | 0,30 | 0,05 | 0,12 | 0,13 | 0,20 | ||||
| 0,10 | 0,12 | 0,19 | 0,23 | 0,12 | 0,20 |
СПИСОК ЛИТЕРАРУРЫ
1. Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М., 2000.
2. Кремер Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер. – М., 2005.
3. Гмурман В.Е Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. – М., 1997.
4. Сборник задач по высшей математике для экономистов: Учеб. пособие / Под ред. В.И. Ермакова. – М.: ИНФА, 2003.
СОДЕРЖАНИЕ
1. СЛУЧАЙНЫЕ СОБЫТИЯ………………………………………………..3
1.1. Множество событий. Классическое определение вероятности
события……………………………………………………………………….3
1.2. Теоремы сложения и умножения вероятностей………………………4
1.3. Вероятность появления хотя бы одного события…………………….6
1.4. Формула полной вероятности и формула Байеса…………………….7
1.5. Формулы Бернулли и Пуассона………………………………………..8
2. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ…………………………..9
2.1. Закон распределения вероятностей……………………………………9
2.2. Математическое ожидание и дисперсия……………………………...12
3. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ……………………….14
3.1. Функция распределения вероятностей и плотность вероятности…..14
3.2. Математическое ожидание и дисперсия. Мода и медиана………….16
3.3. Равномерное распределение…………………………………………..17
3.4. Нормальное распределение…………………………………………...18
3.5. Показательное распределение………………………………………...19
4. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН………………………………..20
4.1. Законы распределения двумерной случайной величины…………...20
4.2. Числовые характеристики системы двух случайных величин……..22
ПРАКТИКУМ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ…………………………24
Задания………………………………………………………………………24
СПИСОК ЛИТЕРАТУРЫ………………………………………………….30
Составители: ИЗМАЙЛОВ Шамиль Зинурович
САФИН Рашит Рафаилович
Методические указания
для самостоятельного изучения
дисциплины «Математика»
с контрольными заданиями
Раздел III
«Теория вероятностей»
Технический редактор: С.А. Юдина
Подписано в печать 02.02.09. Формат 60×84 1/16.
Бумага писчая. Гарнитура «Таймс».
Усл. печ. л. 1,86. Уч.-изд. л. 2. Тираж 100 экз.
Цена свободная. Заказ № 13.
Отпечатано с готовых авторских оригиналов
на ризографе в издательском отделе
Уфимской государственной академии экономики и сервиса
450078, г. Уфа, ул. Чернышевского, 145; тел. (347) 241-69-85.
