Формулировка и математич.модельтрансп.задачи(ТЗ) по критерию стоимости. Особенности модели как ЗЛП.

У mпоставщиков А1, А2, …, Аm имеется a1, a2, …,am единиц однородного груза, к-рыйд.б.доставленnпотребителям В1, В2, …, Вn в количествах b1, b2,…,bn. Известна стоимость( 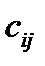) доставки ед-цы груза из пункта Ai в пункт Bj (j=от 1 до m). Необходимо найти такой план транспорт-кипрод-ии при к-ром суммарные затраты минимальны. Обозначим ч/з xij объем перевозки груза из i-го пункта в j-ый (i=от 1 до m; j=от 1 доn). Тогда матрица 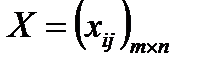и есть план транспортировки грузаУдельные трансп.издержкизапис-ся в форме матрицы С=[cij]m *n и наз-ся она матрицей тарифов.

Экономико-матем.модель ТЗ должна отражать все условия и цель задачи в математич.форме. Переменные xij(i=от 1 до m;j=от 1 до n) должны удовлетворять ограничениям по запасам, потребностям и условиям неотрицательности:

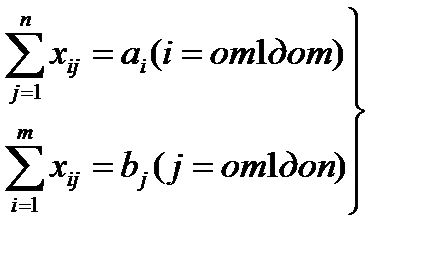(1)

xij>=0 (i=от 1 до m; j=от 1 до n) (2)

Цель ТЗ – минимизировать общие затраты на реализацию плана перевозок, к-рые можно представить функцией

f=c1.1 x1.1+c1.2 x1.2+…+c1.nx1.n+…+cm.1 xm.1+cm.2 xm.2+…+ cm.nxm.n=(i=от 1 до m)Σ(j=от 1 до n)Σcijxij. (3)

Математически ТЗ ставится так. Даны система ограничений (1) при условии (2) и линейная функция (3). Требуется среди множ-ва решений системы (1) найти такое неотрицат.решение, при к-ром линейная функция (3) принимает минимальное значение. План перевозок 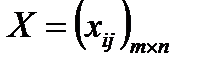называется допустимым, если он удовлетворяет ограничениям (1) и (2). Допустимый план перевозок, доставляющий минимум целевой функции (3), наз-сяоптимальным.

Теорема: для того чтобы ТЗ имела допустимые планы, необходимо и достаточно выполнение равенства

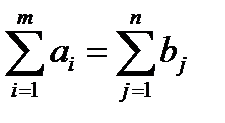(4)

Если равенство не выполняется, в задачу вводится фиктивный пославщик или потребитель.

21. ТЗ с открытой и закрытой моделью. Преобразование открытой модели в закрытую модель.

Модель ТЗ наз-ют закрытой, если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т.е. выполняется равенство

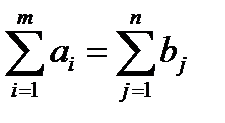
Если для ТЗ выполняется одно из условий:

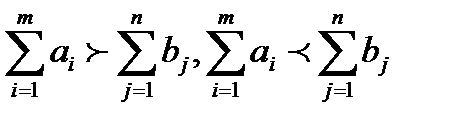
То модель наз-ют открытой.

Для разрешимости ТЗ с открытой моделью необходимо преобразовать ее в закрытую. Так, при выполнении первого условия необходимо ввести фиктивный (n+1)-й пункт назначения 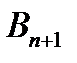, т.е. в матрице задачи предусматривается дополнительный столбец. Спрос фиктивного потребителя полагают равным небалансу, т.е. 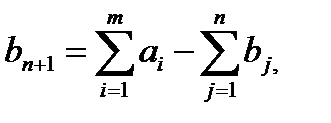а все тарифы – одинаковыми, чаще всего равными нулю, т.е. 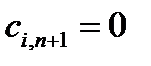(i=от 1 до m). Аналогично при выполнении второго условия вводится фиктивный поставщик 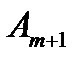, запас груза у которого равен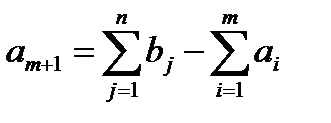

А тарифы дополнительной строки распределительной таблицы равны нулю, т.е. 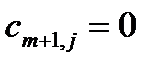(j=от 1 до n)

При преобразовании открытой задачи в закрытую целевая функция не меняется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю.

22. условие разрешимости ТЗ. Условие целочисленности оптимального плана.

Для разрешимости поставленной задачи необходимо и достаточно, чтобы сумма запасов продукта равнялась сумме спроса на него, т.е.