Интегрирование дробно рациональных функций

Если под знаком интеграла стоит правильная рациональная дробь, то, после разложения ее на простейшие, мы получим интегралы следующих четырех типов:

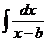(тип I), 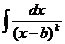(тип II), 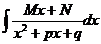(тип III), и 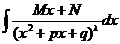(тип IV),

и если мы научимся вычислять эти интегралы, мы сможем найти интегралы от любых дробно рациональных функций.

Итак:

Тип I. Делая замену переменных 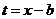, , 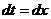получим:

.

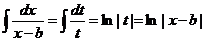Тип II. Делая замену переменных 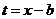, , 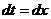получим:

.

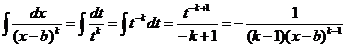Тип III.

Имеем .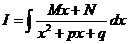

Выделим в знаменателе полный квадрат

,

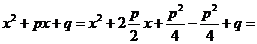
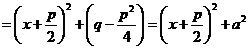где 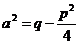. Тогда получаем

.

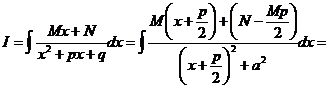
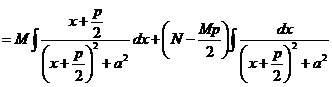В первом интеграле сделаем замену переменных 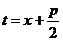. Тогда

.

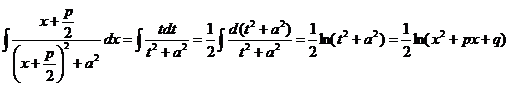Во втором интеграле, после той же замены переменных, получим

.

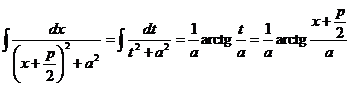Сводя все вместе и упрощая, получим

,

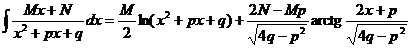что и дает явное выражение для интеграла третьего типа.

Тип IV. Мы не будем выводить выражение для интегралов этого типа - оно очень громоздкое и носит рекуррентный характер. При желании, Вы можете найти его в справочниках или в более подробных курсах по математическому анализу. Для нас принципиальным является лишь то, что все эти интегралы выражаются через элементарные функции, и поэтому неопределенный интеграл от дробно рациональной функции всегда может быть вычислен (хотя и с большими трудностями).

Интегралы от тригонометрических функций

Основная идея всего дальнейшего - свести изучаемые классы интегралов к интегралам от дробно рациональных функций. Это производится при помощи вполне определенных замен переменных, называемых далее подстановками. Поэтому дальнейшее изложение выглядит так: указывается подстановка, условия ее применимости и доказывается, что данная подстановка приводит рассматриваемый интеграл к интегралу от дробно рациональной функции.

Определение. Полиномом от двух переменных степени п называется выражение

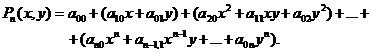
(Обратите внимание, как индексы у коэффициентов а соотносятся со степенями х и y).

Пусть 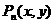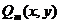- два полинома от двух переменных. Функция 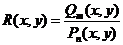называется дробно рациональной функцией двух переменных.

В этом разделе будут рассмотрены вопросы вычисления интегралов вида

.

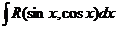Для их вычисления используют четыре подстановки.

Универсальная подстановка

Эта подстановка имеет вид .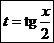

Докажем, что она приводит рассматриваемый класс интегралов к интегралам от дробно рациональных функций. Имеем:

;

;

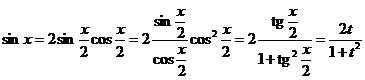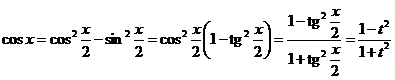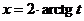Þ .

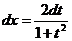В результате рассматриваемый интеграл принимает вид

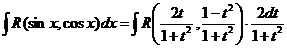
и он является интегралом от дробно рациональной функции, который вычисляется при помощи разложения на простейшие.

Упрощенные подстановки

Универсальная подстановка потому и называется универсальной, что позволяет любыеинтегралы рассматриваемого типа сводить к интегралам от дробно рациональных функций. Однако, получающиеся при этом интегралы обычно достаточно сложны. Поэтому ее следует использовать только в том случае, если нельзя применить так называемые упрощенные подстановки, к рассмотрению которых мы и переходим. Их всего три.

1. Условие применимости первой упрошенной подстановки имеет вид

.

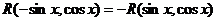Чтобы изложение дальнейшего было короче, будем писать u вместо 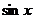и v вместо 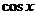. Тогда условие применимости первой упрощенной подстановки примет вид .

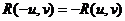Но в нашей формуле, определяющей функцию 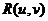и в числителе и в знаменателе стоят полиномы по переменным и и v. Когда же функция 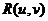будет нечетной функцией по переменной и? Легко догадаться, что это будет тогда, когда сомножитель и можно вынести за скобки и, после этого, в числителе и знаменателе останутся лишь полиномы от переменной и², то есть тогда, когда функция 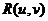может быть приведена к виду .

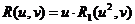Это условие и определяет первую упрощенную подстановку. Она имеет вид

.

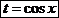Тогда 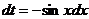и мы имеем

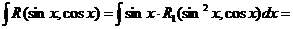
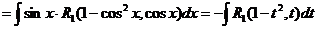
и мы получили интеграл от дробно рациональной функции.

2. Условие применимости второй упрошенной подстановки имеет вид

.

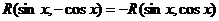Повторяя почти дословно все рассуждения, касающиеся первой упрощенной подстановки, можно получить, что в этом случае функция 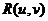может быть приведена к виду .

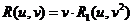Вторая упрощенная подстановка имеет вид 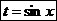. Тогда 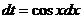и мы имеем

=

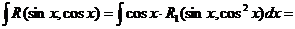
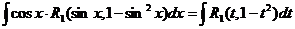
и мы получили интеграл от дробно рациональной функции.

2. Условие применимости третьей упрошенной подстановки имеет вид

.

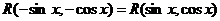Попытаемся сообразить, что это дает относительно вида функции 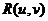. Прежде всего имеем

.

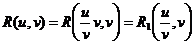Тогда условие применимости третьей упрощенной подстановки дает

.

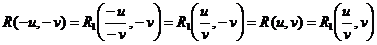Используя те же рассуждения, что и выше, легко догадаться, что второй аргумент у 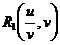должен содержать только четныестепени v. Поэтому 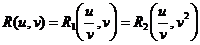, и

.

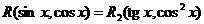Это и определяет третью упрощенную подстановку. Она имеет вид 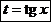. Действительно, в этом случае

, , ,

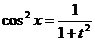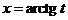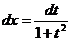и наш интеграл принимает вид

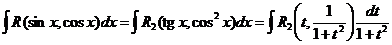
и мы получили интеграл от дробно рациональной функции.

6.11 Вычисление интегралов вида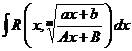

Рассмотрим вычисление интегралов вида 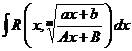при условии 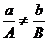(очевидно, что если имеет место равенство, то под знаком корня дробь сократится, и будет просто интеграл от дробно рациональной функции).

Все, что здесь надо запомнить - это то, какую замену переменных (подстановку) здесь нужно сделать, а именно

.

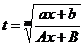Дальше все идет само собой. Выражаем х через t

, , ,

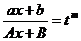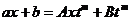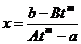и самое неприятное - корень - исчез.

Далее имеем

.

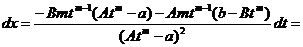
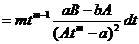Заметим, что .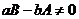

Окончательно получаем

,

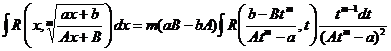и мы получили интеграл от дробно рациональной функции.

6.12 Вычисление интегралов вида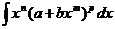

Рассмотрим теперь вычисление интегралов вида 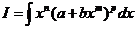,где т, п, и р - рациональныечисла.

Рассмотрим четыре возможных случая.

1. р - целое положительноечисло.

Тогда следует комбинацию 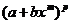раскрыть по формуле бинома Ньютона, раскрыть скобки и проинтегрировать почленно.

2. р - целое отрицательноечисло.

Вспомним, что т и п - рациональныечисла. Это значит, что они представимы в виде 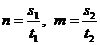. Пусть r есть наименьшее общее кратноечисел t₁ и t₂. Тогда .

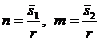Теперь сделаем замену переменных 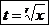. Тогда получаем

, , ,

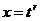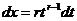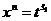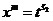
и рассматриваемый интеграл принимает вид

,

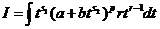и степени у t всюду целые числа и мы получили интеграл от дробно рациональной функции.

3. Комбинация 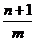- целое число.

Пусть 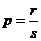. Тогда надо сделать следующую замену переменных

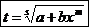
(обратите внимание, откуда в показателе корня взялось это s!).

А теперь проделаем аккуратно все выкладки. Сначала выразим х через t:

; .

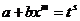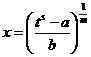Теперь найдем dx

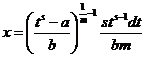
и подставим все это в изучаемый интеграл

.

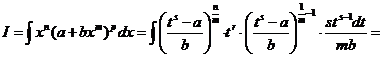
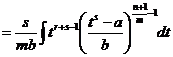Но 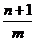- целое число! Все остальные степени также целые числа. Поэтому под знаком интеграла стоит дробно рациональная функция и интеграл вычисляется методом разложения подынтегральной функции на простейшие.

4. Комбинация 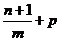- целое число.

Пусть снова 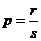. Тогда надо сделать следующую замену переменных

.

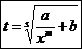А теперь проделаем аккуратно все выкладки. Сначала выразим х через t:

; .

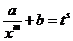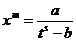Дифференцируем последнее соотношение

.

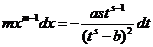Попытаемся переписать подынтегральное выражение так, чтобы в нем была явно видны комбинации, равные 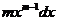и t:

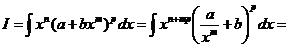
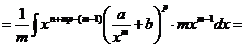
Заметим теперь, что

,

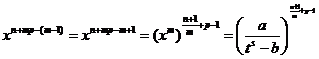так что, продолжая предыдущую строку, получаем

.

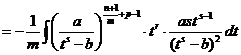Но 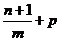- целое число. Все остальные степени также целые числа. Поэтому под знаком интеграла стоит дробно рациональная функция и интеграл вычисляется методом разложения подынтегральной функции на простейшие.

Как показал знаменитый русский математик П.Л. Чебышёв, во всех остальных случаях рассматриваемый интеграл через элементарные функции не выражается.

6.13 Вычисление интегралов вида 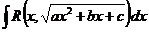. Подстановки Эйлера

Рассмотрим теперь вычисление интегралов вида 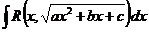.Они находятся с помощью так называемых подстановок Эйлера. Вообще-то их три, но мы рассмотрим только две - первую и третью.

Первая подстановка Эйлера

Эту подстановку можно применять, если выполнено условие 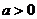. Она имеет вид

.

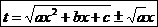Проделаем все вычисления, взяв, для определенности, знак +. Тогда

.

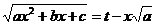Возводим это выражение в квадрат

,

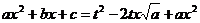сокращаем 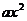и выражаем в явном виде х через t:

.

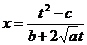Теперь можно выразить через t и комбинацию 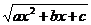. Имеем

,

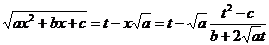и корень исчезает. Далее,

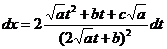
и подстановка всего этого в исходный интеграл приводит его к виду

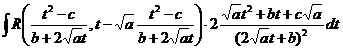
и под знаком интеграла стоит дробно рациональная функция от переменной t.

Третья подстановка Эйлера.

Условие применимости этой подстановки: полином 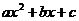имеет действительные корних₁ и х₂.

Сама третья подстановка Эйлера имеет вид

.

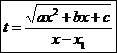Покажем, что она сводит наш интеграл к интегралу от дробно рациональной функции. Так как 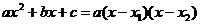, то

.

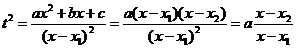Отсюда находится х через t:

.

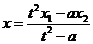Для комбинации 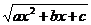получаем

,

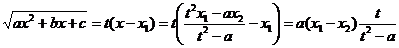и корень исчезает. Легко получить, что

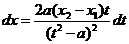
и рассматриваемый интеграл приводится к виду

,

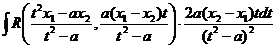и под знаком интеграла снова получилась дробно рациональная функция от переменной t.

Как видно из приведенных ниже рисунков, эти две подстановки исчерпывают все возможные случаи.

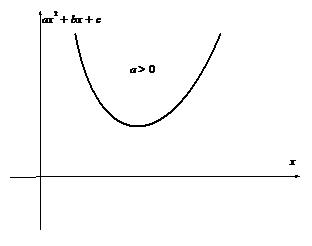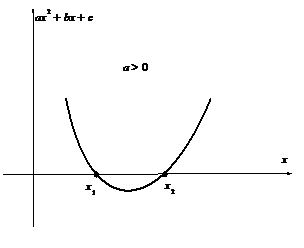Применима первая подстановка Эйлера	Применимы первая и третья подстановки Эйлера

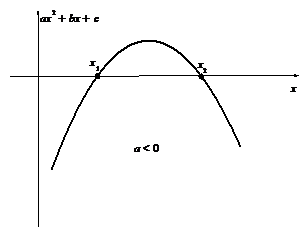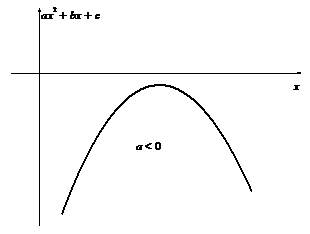Применима третья подстановка Эйлера	Подкоренное выражение всегда отрицательно, поэтому интеграл не имеет смысла.

Заметим в заключение, что если 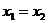, то 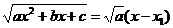и никаких иррациональностей нет.