Формула Эйлера. Показательная форма комплексного числа

Вспомним ряды Тейлора

,

,

.

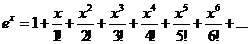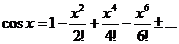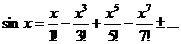Далее заметим, что 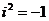, , 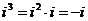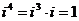и далее все повторяется.

Найдем теперь 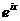. Имеем

.

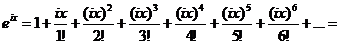
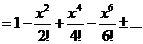
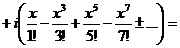
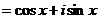Мы получили знаменитую формулу Эйлера

.

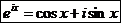Полезно помнить некоторые следствия из этой формулы. Заменяя в ней i на -i, получим

.

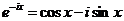Складывая и вычитая эти две формулы, получим

, .

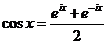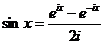Вспоминая гиперболические функции, можем записать:

, ,

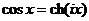что говорит о родстве этих функций.

Вернемся к комплексным числам. Имеем

,

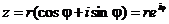что и дает так называемую показательную форму комплексного числа. Так как аргумент j определяется с точностью до слагаемого 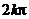, то, в общем случае,

, .

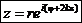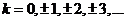Эта формула позволяет определить логарифм комплексного числа:

, .

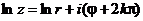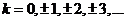Заметим, что логарифм - бесконечнозначная функция.

В частности, 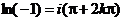, , 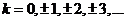так как 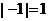и .

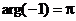6.6 Разложение полиномов (многочленов) на сомножители

Выражение

,

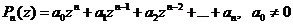называется полиномом или многочленом от переменной z степени п. Полином степени 0 - это константа ( ).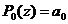

В дальнейшем мы будем считать, что переменная 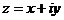комплексная,а коэффициенты 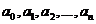- действительныечисла.

Пусть 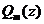есть полином от переменной z степени т<п. Тогда имеет место представление

,

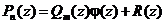где полином 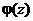(его степень равна 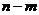) называется частнымполиномов 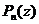и 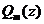, а полином 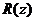- остаткомот деления 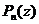на 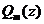. Степень остатка не выше 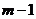. Обычно операция деления осуществляется столбиком, и как это делать - учат в школе.

Если 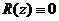, то говорят, что полином 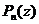делится на .

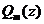Корни полинома

Определение.Число b (действительное или комплексное) называется корнемполинома 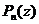, если .

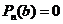Теорема 1. Для того, чтобы b было корнем полинома 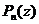,необходимо и достаточно, чтобы 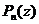делилось на .

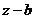Доказательство.

По сказанному выше, имеем

,

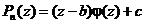где с - полином степени 0, то есть константа. Тогда

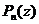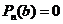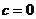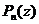1. Если b есть корень , то , откуда следует, что и делится на .

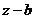2. Если 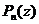делится на 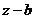, то 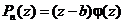и тогда 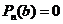, то есть b корень полинома . <

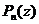Теорема 2. Пусть корень полинома b есть комплексное число. Тогда комплексно сопряженное число 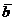также является корнем этого полинома.

Доказательство.

1. Докажем сначала, что 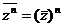. Имеем

,

,

.

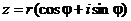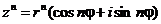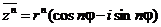С другой стороны

,

.

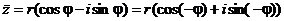2. Так как по условию все коэффициенты полинома есть действительные числа, то .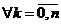

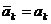3. Поэтому, если

,

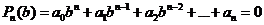то

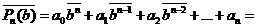
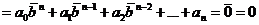
и 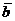также есть корень полинома . <

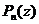Таким образом, комплексные корни полинома всегда «ходят парами»: если 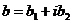есть корень, то 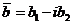- тоже корень.

Основная теорема алгебры. Всякий полином степени п ³ 1 имеет хотя бы один корень (действительный или комплексный).

Доказывать эту теорему мы не будем - все-таки это курс математического анализа, а не алгебры.

Теорема 3. Полином степени п имеет ровно п корней.

Доказательство.

Рассмотрим полином 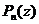. Тогда, по основной теореме алгебры, 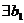такое, что 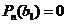и поэтому имеет место разложение .

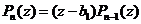Рассмотрим полином 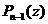. Тогда, по основной теореме алгебры, 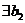такое, что 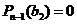и поэтому имеет место разложение .

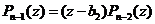Рассмотрим полином 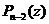. Тогда, по основной теореме алгебры, 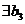такое, что 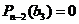и поэтому имеет место разложение .

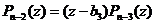И т.д., и т.д., и т.д.

Заметим, что каждый раз степень полинома уменьшается на 1. В конце концов, на п-м шаге мы дойдем до полинома степени 0 и получим такое разложение

.

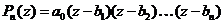Других корней у этого полинома нет, так если z не совпадает с каким-то из 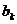, то все сомножители вида 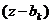отличны от нуля и . <

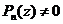Определение.Если в разложении 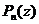на сомножители бином 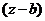повторяется k раз, то говорят, что корень b имеет кратность k.

Если k = 1, то корень называется простым.

Заметим еще, что в паре комплексно сопряженных корней оба корня имеют одинаковую кратность.