Супремум и инфимум числовых множеств.

Выше было описано правило, устанавливающее признак равенства двух вещественных чисел. Опишем теперь правило, позволяющее установить, какое из двух вещественных чисел больше.

1. Пусть оба вещественных числа имеют знак +.

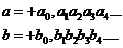
Найдем первую по порядку цифру в этих числах, которые не равны друг другу. Пусть это будет цифра с номером n, то есть

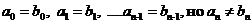
(заметим, что символами математики это записывается так: 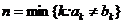). Тогда, если 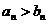, то считаем, что a>b, а если 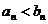, то a<b.

2. Если вещественные числа а и b разных знаков, то большим считается число, имеющее знак +.

3. Пусть оба числа имеют знак –. Назовем модулем вещественного числа это же число, но со знаком +:

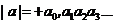
Тогда, если |a|>|b| то считаем, что а<b, если же |a|<|b| то считаем, что а>b.

Это правило будет необходимо нам ниже.

Определение. Множество, элементами которого являются вещественные числа, называется числовым множеством.

Числовые множества мы будем обозначать {x}, где под х будут пониматься вещественные числа.

Для того, чтобы все дальнейшие определения и теоремы записывались в принятой математической форме, введем специальные значки, которые носят название кванторов. Их два:

Знак 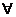называется «квантор общности» и читается «для каждого», «для любого» ( 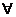есть перевернутая буква А из английского выражения «for All»).

Знак 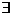называется «квантором существования» и читается «существует» ( 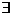есть перевернутая буква Е из английского слова «Exist»). Вариантом этого квантора является знак 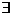!, который читается «существует единственный» или «существует один и только один».

А теперь перейдем к определениям.

Определение 1. Числовое множество {x} называется ограниченным сверху, если 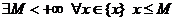(читается: существует такое 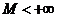, что для любого 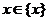выполнено условие x £ M). Число М называется верхней гранью числового множества {x}.

Определение 2. Числовое множество {x} называется ограниченным снизу, если 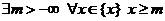. Число m называется нижней гранью числового множества {x}.

Определение 3. Числовое множество {x} называется ограниченным, если .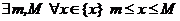

Очевидно, что если, скажем, существует одна верхняя грань, то их бесконечно много: если, например, М – верхняя грань числового множества {x}, то М+1, М+2, М+3 и т.д. – также верхние грани для {x}.

Определение 4. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества {x} (обозначение sup{x}).

Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества {x} (обозначение inf{x}).

Эти понятия столь важны, что опишем их в других терминах.

sup{x} определяется двумя свойствами:

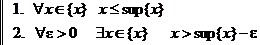
Первое свойство означает, что sup{x} – верхняя грань, то есть все элементы {x} не превосходят sup{x}.

Второе свойство означает, что любая попытка уменьшить эту верхнюю грань приводит к появлению элемента из {x}, который окажется больше .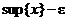

Говоря образно, sup{x} это планка, перепрыгнуть которую нельзя, но любая попытка опустить эту планку хоть чуть-чуть приводит к тому, что кто-то ее преодолевает.

Аналогично, inf{x} определяется двумя свойствами:

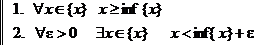
Заметим, что сами sup{x} и inf{x} могут как принадлежать, так и не принадлежать множеству {x}.

Теперь мы в состоянии доказать важнейшую теорему этого раздела и одну из важнейших теорем всего математического анализа.

Теорема о существовании супремума и инфимума.

Если числовое множество {x} не пусто и ограничено сверху, то у него существует sup{x}.

Если числовое множество {x} не пусто и ограничено снизу, то у него существует inf{x}.

Доказательство.

Мы докажем эту теорему только для sup{x} при одном дополнительном предположении – в множестве {x} имеются положительные числа. Доказательство разбивается на три части.

1. Процедура построения sup{x}.

Пусть М – верхняя грань для {x}, то есть 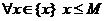. Проделаем следующее построение:

а) Выбросим из множества {x} все отрицательные числа.

б) У оставшихся чисел выпишем те цифры 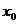, которые стоят перед запятой. Множество 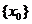этих цифр конечно, так как этих цифр не более чем [M] (целая часть М). Обратите внимание, что именно в этом месте используется ограничение теоремы – существование верхней грани. Если бы верхней грани не существовало, то множество {x} было бы бесконечным.

В силу конечности множества 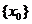из этих цифр до запятой можно выбрать самую большую -–ведь их же конечное число. Обозначим самую большую из этих цифр через .

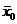в) Выбросим из {x} все те числа, у которых цифра до запятой меньше 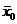. У оставшихся чисел выпишем первую цифру после запятой. Этих цифр 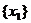не более 10. Выберем из них самую большую и обозначим ее через .

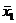г) Выбросим из {x} все те числа, у которых первая цифра после запятой меньше 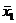. У оставшихся чисел выпишем вторую цифру после запятой. Этих цифр 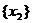не более 10. Выберем из них самую большую и обозначим ее через .

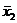д) Выбросим из {x} все те числа, у которых…

Повторяя эту операцию до бесконечности мы построим число

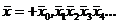
Покажем, что 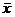и есть sup{x}.

2. Проверим первое свойство sup{x}.

Возьмем любое 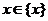. Если х имеет знак –, то ясно, что .

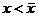Пусть х имеет знак +. Тогда

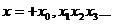
Сравним х₀ и 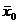. Вспомним, что 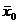было самым большим из 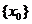. Поэтому может быть всего два варианта: либо 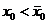, либо 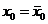. В первом случае 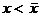и дальнейшая проверка ни к чему. Если же 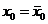, то сравним х₁ и 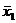. Опять-таки по построению возможны два варианта: либо 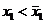и тогда 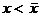и дальнейшая проверка ни к чему, либо .

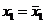Если 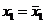, то сравним х₂ и 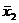. Опять-таки по построению возможны два варианта: либо 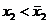и тогда 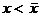и дальнейшая проверка ни к чему, либо .

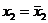Продолжая этот процесс и дальше, получим, что возможны два следующих варианта.

а) Найдется какое-то n, для которого 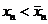. Тогда .

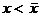б) Для всех n 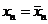. Тогда .

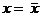Поэтому всегда 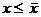и первое свойство супремума выполнено.

Эту процедуру можно пояснить следующей диаграммой:

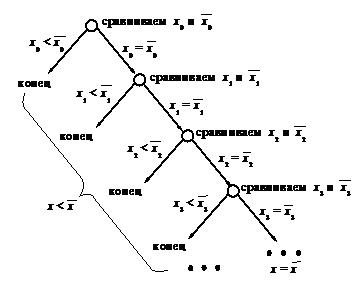
3. Проверка второго свойства супремума.

Заметим, что второе свойство 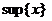можно записать так: 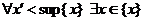такой, что .

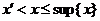Возьмем положительное :

.

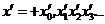Так как , то найдется такое n, что

.

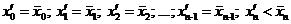Но вспомним процедуру построения 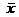. На n-м шаге после выбрасывания во множестве {x} оставались лишь те числа, для которых 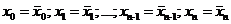. Любое из этих чисел будет больше x' (так как 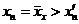), но естественно, меньше или равно 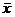. Поэтому любое из этих чисел удовлетворяет второму свойству супремума. <

Подумайте сами, что надо изменить в процедуре построения 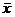, если во множестве {x} есть только отрицательные числа.