Определение и геометрический смысл производной
Глава 4. Производная
Определение и геометрический смысл производной
Пусть функция 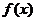 непрерывна в точке
непрерывна в точке 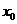 .
.
Определение. Производной от функции 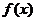 в точке
в точке 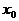 называется величина
называется величина
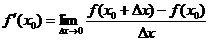 .
.
Дадим некоторые расшифровки этого важнейшего понятия математического анализа.
а) Вспоминая определение предела, можно записать определение 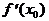 через кванторы
через кванторы 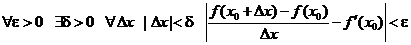 .
.
б) Величина 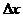 называется приращением аргумента, а величина
называется приращением аргумента, а величина 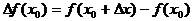 приращением функции. Тогда
приращением функции. Тогда
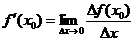 .
.
в) Обозначая 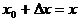 , можно записать
, можно записать
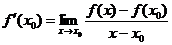 .
.
Понятие производной впервые появилось в физике в связи с понятием скорости. Пусть некоторая материальная точка движется по оси 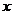 так что
так что 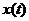 есть координата точки в момент времени
есть координата точки в момент времени 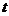 . Спустя время
. Спустя время 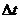 координата точки будет
координата точки будет 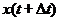 , т.е. за время
, т.е. за время 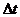 точка пройдет путь
точка пройдет путь 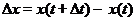 . Поэтому средняя скорость точки за интервал времени
. Поэтому средняя скорость точки за интервал времени 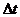 будет равна
будет равна 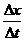 . Чтобы найти мгновенную скорость точки в момент времени
. Чтобы найти мгновенную скорость точки в момент времени 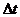 надо устремить
надо устремить 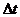 к нулю, то есть
к нулю, то есть
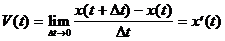 .
.
Таким образом, производная от координаты точки определяет ее мгновенную скорость. Поэтому и производную функции 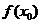 в некоторой точке
в некоторой точке 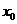 можно трактовать как скорость изменения функции в этой точке.
можно трактовать как скорость изменения функции в этой точке.
Дадим еще геометрический смысл производной. В определение производной входят две операции: деление 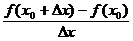 и предельный переход при
и предельный переход при 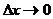 . Что же это дает? Нанося на график точки с координатами (
. Что же это дает? Нанося на график точки с координатами ( 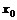 ,
, 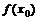 ) и (
) и ( 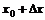 ,
, 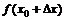 ) мы получим фигуру изображенную на рисунке. Проведем через эти точки линию, которая называется секущей. Тогда дробь
) мы получим фигуру изображенную на рисунке. Проведем через эти точки линию, которая называется секущей. Тогда дробь 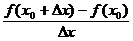 есть не что иное как
есть не что иное как 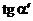 , где
, где 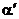 есть угол наклона секущей к оси OX.
есть угол наклона секущей к оси OX.

Но в определении производной есть еще предельный переход при 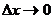 . Что же дает этот предельный переход?.
. Что же дает этот предельный переход?.
При 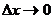 точка M начинает двигаться к точке M0. При этом вся секущая будет поворачиваться около точки M0 и в пределе она превратиться в касательную к точке M0. Угол
точка M начинает двигаться к точке M0. При этом вся секущая будет поворачиваться около точки M0 и в пределе она превратиться в касательную к точке M0. Угол 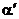 при этом перейдет в угол
при этом перейдет в угол 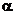 , который эта касательная образует с осью х. Поэтому можно утверждать, что
, который эта касательная образует с осью х. Поэтому можно утверждать, что
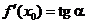 ,
,
где 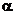 - угол, образованный касательной к кривой в точке
- угол, образованный касательной к кривой в точке 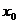 и осью OX.
и осью OX.
Алгебра производных
Выведем важнейшие формулы, касающиеся вычисления производных. В дальнейшем 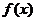 и
и 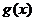 - некоторые функции, у которых существуют
- некоторые функции, у которых существуют 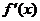 и
и 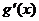 , а с - некоторая константа (число).
, а с - некоторая константа (число).
1. 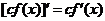 .
.
Доказательство.
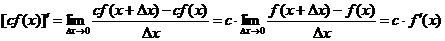 .
.
2. 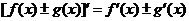 .
.
Доказательство
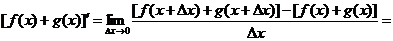
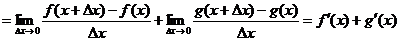
Аналогично выводится формула для 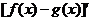 .
.
3. 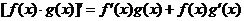 .
.
Доказательство
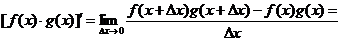
(В числителе дроби прибавим и вычтем комбинацию 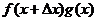 )
)
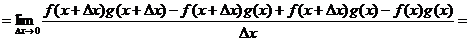
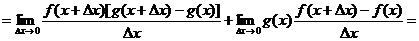
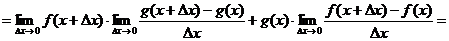
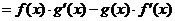
4. 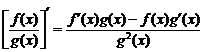 .
.
Доказательство
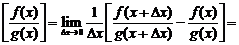
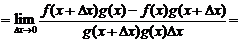
(прибавляем и вычитаем в числителе комбинацию 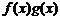 )
)
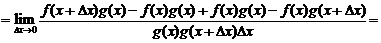
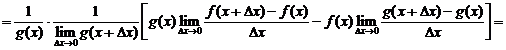
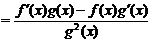
5. 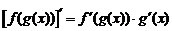 .
.
В выражении 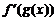 подразумевается, что производная от функции
подразумевается, что производная от функции 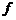 берется так, как будто
берется так, как будто 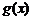 является единым целым (аргументом).
является единым целым (аргументом).
Доказательство
Пусть аргумент 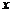 получил приращение
получил приращение 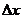 . Тогда функция
. Тогда функция 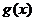 получила приращение
получила приращение 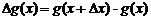 так что
так что 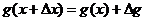 . Поэтому
. Поэтому
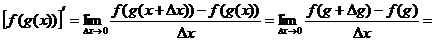
(делим и умножаем дробь на 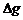 )
)
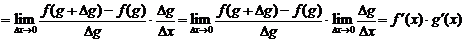 .
.
6. 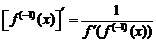
Доказательство
Пусть 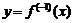 так что
так что 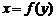 . Если аргументу x дать приращение
. Если аргументу x дать приращение 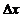 , то величина
, то величина 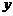 получит приращение
получит приращение 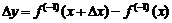 . Поэтому
. Поэтому
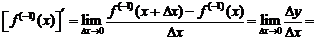
= 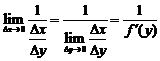
Однако в данной формуле есть одна неувязка. Слева стоит функция от 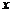 , а справа получилась функция от
, а справа получилась функция от 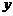 . Чтобы устранить это несоответствие надо в правой части заменить
. Чтобы устранить это несоответствие надо в правой части заменить 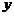 на
на 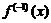 . Тогда получим окончательно
. Тогда получим окончательно
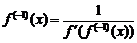 .
.
7. 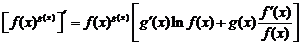
Вывод этой формулы следует разбирать после прочтения следующего параграфа.
Доказательство
Обозначим 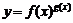 . Тогда
. Тогда 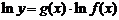 . Вычисляя производную от обеих частей этого равенства, получим
. Вычисляя производную от обеих частей этого равенства, получим
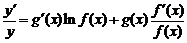 .
.
Отсюда
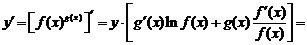
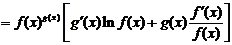 .
.
Вместо того чтобы запоминать эту формулу лучше запомнить правило: для того чтобы вычислить производную от 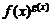 , надо это выражение сначала прологарифмировать.
, надо это выражение сначала прологарифмировать.
Все эти формулы сведены в следующую таблицу, которую следует запомнить (кроме последней формулы).
Таблица 1.
| Функция | Производная |
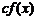 | 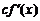 |
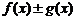 | 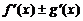 |
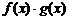 | 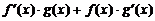 |
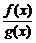 | 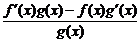 |
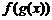 | 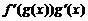 |
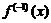 | 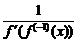 |
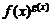 | 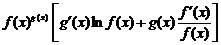 |
Таблица производных
Выведем теперь таблицу производных от элементарных функций
1. 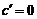
Действительно, если  , то
, то
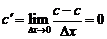 .
.
2. 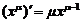
Имеем
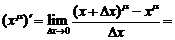
(вынесем вверху 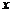 за скобки)
за скобки)
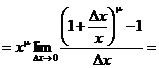
(Сделаем «замену переменных» 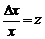 . Тогда
. Тогда 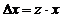 и )
и )
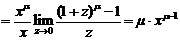 ,
,
где был использован замечательный предел.
Рекомендуется запомнить некоторые частные случаи этой формулы
а) 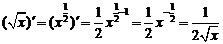
б) 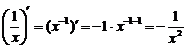
3. 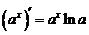
Имеем
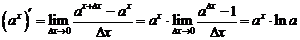 ,
,
где был использован замечательный предел
Особенно простой результат получается при 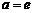
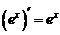
4. 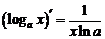
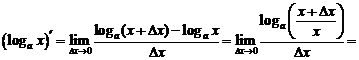
сделаем «замену переменных» 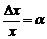 . Тогда
. Тогда 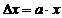 и
и
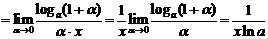
Особенно простой результат получается при 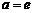
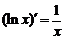
5. 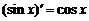
Имеем
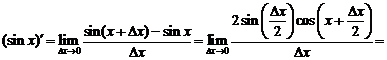
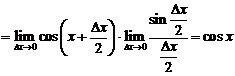 .
.
где также был использован замечательный предел.
6. 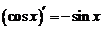 .
.
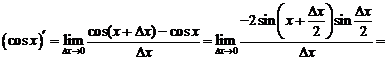
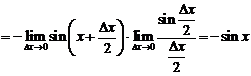
7. 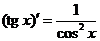 .
.
Так как 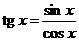 , то
, то
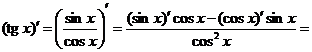
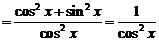 .
.
8. 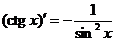 .
.
Вывод аналогичен
9. 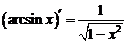
В данном случае 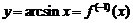 и
и 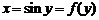 , то есть
, то есть 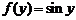 . Поэтому
. Поэтому
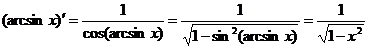 .
.
10. 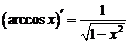
Вывод аналогичен.
11. 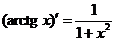 .
.
В данном случае 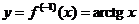 и
и 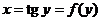 , то есть
, то есть 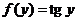 . Поэтому
. Поэтому
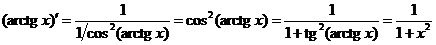 .
.
12. 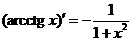 .
.
Вывод аналогичен.
13. 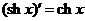
Действительно
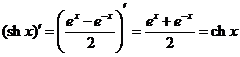 .
.
14. 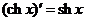 15.
15. 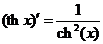 .
.
Вывод аналогичен
Все эти формулы сведены в таблицу, которую следует заучить
Таблица 2
| функция | производная | функция | производная |
1. 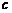 |  | 7. 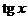 | 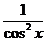 |
2. 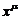 | 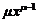 | 8. 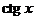 | 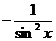 |
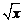 | 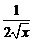 | 9. 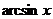 | 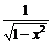 |
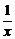 | 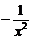 | 10. 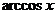 | - 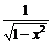 |
3. 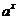 | 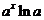 | 11. 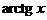 | 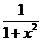 |
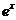 | 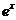 | 12. 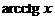 | 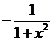 |
4. 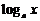 |  | 13. 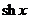 | 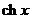 |
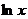 | 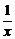 | 14. 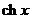 | 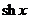 |
5. 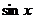 | 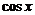 | 15. 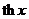 | 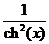 |
6. 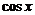 | 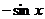 |
Особые случаи
То, что в точке 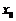 функция
функция  непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?
непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?
Односторонние производные
Назовем
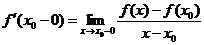
производной от функции  в точке
в точке 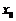 слева, а
слева, а
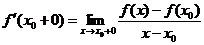
 | производной в той же точке справа. Разумеется, если 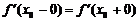 , то это означает, что в точке , то это означает, что в точке 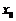 существует существует 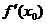 . Но могут быть случаи, когда . Но могут быть случаи, когда 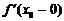 и и 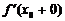 существуют, но не равны друг другу. В этом случае не существует и существуют, но не равны друг другу. В этом случае не существует и 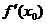 . График функции . График функции  имеет в точке имеет в точке 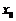 в этом случае «излом», и в этой точке к графику можно провести две касательные (см. рисунок). в этом случае «излом», и в этой точке к графику можно провести две касательные (см. рисунок). |
Бесконечная производная
 | Рассмотрим функцию 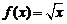 определенную для определенную для 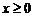 и потребуем найти и потребуем найти 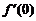 . Имеем . Имеем 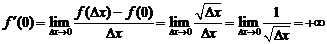 и производная равна и производная равна 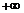 . Рассматривая график функции . Рассматривая график функции 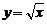 легко увидеть, что это означает просто то, что в точке легко увидеть, что это означает просто то, что в точке 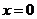 касательная к графику параллельна оси OY. касательная к графику параллельна оси OY. |
Несуществование производной
Наконец, может быть ситуация, когда 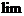 , фигурирующий в определении производной, не существует.
, фигурирующий в определении производной, не существует.
Рассмотрим для примера, 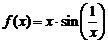 . Так как
. Так как 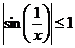 , то
, то 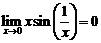 . Поэтому, полагая
. Поэтому, полагая 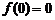 , получим
, получим
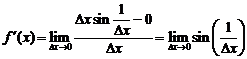 ,
,
и этот предел просто не существует.
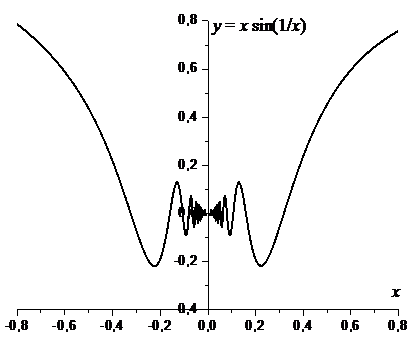 | Из графика функции 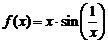 видно, что с приближением к точке видно, что с приближением к точке 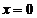 касательная колеблется, не стремясь ни к какому определенному положению. В математике построены даже примеры функций, которые являются непрерывными, но ни в одной точке не имеют производной. касательная колеблется, не стремясь ни к какому определенному положению. В математике построены даже примеры функций, которые являются непрерывными, но ни в одной точке не имеют производной. |
Теорема Ферма
Теорема. Пусть функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке 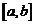 и в некоторой внутренней точке
и в некоторой внутренней точке 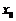 этого промежутка достигает своего наибольшего или наименьшего значения. Если в этой точке существует производная, то она равна нулю:
этого промежутка достигает своего наибольшего или наименьшего значения. Если в этой точке существует производная, то она равна нулю: 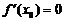 .
.
Доказательство
Пусть, для определенности, в точке 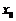 функция
функция  достигает своего наибольшего значения.
достигает своего наибольшего значения.
По условию теоремы эта точка внутренняя, то есть 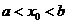 , и поэтому к этой точке можно подойти и слева и справа.
, и поэтому к этой точке можно подойти и слева и справа.
Пусть мы подходим к 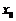 слева. Тогда
слева. Тогда
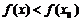 (так как
(так как 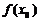 - наибольшее значение);
- наибольшее значение);
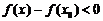 ;
;
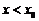 (так как мы подходим слева);
(так как мы подходим слева);
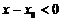 ;
;
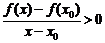 .
.
Делая предельный переход 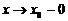 , получим
, получим
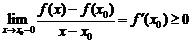 .
.
Пусть мы подходим к точке 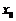 справа. Тогда
справа. Тогда
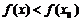 (так как
(так как 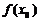 - наибольшее значение);
- наибольшее значение);
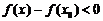 ;
;
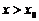 (так как мы подходим слева);
(так как мы подходим слева);
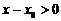 ;
;
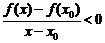 .
.
Делая предельный переход 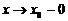 , получим
, получим
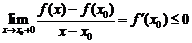 .
.
Совместить два полученных неравенства можно только в одном случае: 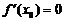 . <
. <
 | Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX. |
Существенность ограничений
В теореме Ферма по сути дела два ограничения: а) точка 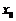 расположена внутри отрезка
расположена внутри отрезка 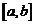 и б)
и б) 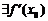 . Покажем, что оба ограничения являются существенными, то есть отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
. Покажем, что оба ограничения являются существенными, то есть отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
а) «внутренность» точки 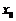 .
.
 | Если максимум или минимум функции  достигается на границе отрезка, то, как видно из рисунка, утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке достигается на границе отрезка, то, как видно из рисунка, утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке 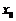 только с одной стороны, и поэтому не получится второго, противоположного неравенства. только с одной стороны, и поэтому не получится второго, противоположного неравенства. |
б) существование производной.
 | Пусть в точке 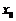 существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства 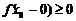 и и 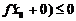 , которые нельзя будет объединить в одно равенство, так как теперь , которые нельзя будет объединить в одно равенство, так как теперь 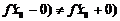 . . |
Теорема Ролля
Пусть функция 
а) определена и непрерывна на 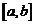 ;
;
б) 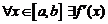 ;
;
в) 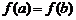
Тогда существует точка 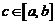 в которой
в которой 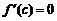 .
.
Доказательство этой теоремы следует из такой логической цепочки рассуждений:
1. Так как  определена и непрерывна на
определена и непрерывна на 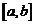 , то, по первой теореме Вейерштрасса, она ограничена на
, то, по первой теореме Вейерштрасса, она ограничена на 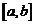 , то есть существуют конечные
, то есть существуют конечные 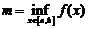 и
и 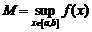 .
.
2. Если 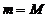 , то
, то  есть константа, то есть
есть константа, то есть 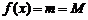 и поэтому
и поэтому 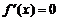
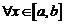 . В качестве точки
. В качестве точки 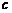 можно взять любую точку из
можно взять любую точку из 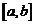 .
.
3. Если 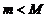 , то, в силу условия
, то, в силу условия 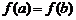 и второй теоремы Вейерштрасса, хотя бы одно из значений
и второй теоремы Вейерштрасса, хотя бы одно из значений 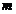 или
или 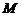 достигается во внутренней точке промежутка
достигается во внутренней точке промежутка 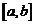 (см. рисунок). По теореме Ферма, в этой точке (их может быть и несколько) производная равна нулю. <
(см. рисунок). По теореме Ферма, в этой точке (их может быть и несколько) производная равна нулю. <
 |  |
| Внутри промежутка достигается sup | Внутри промежутка достигается inf |

Внутри промежутка достигаются и sup и inf.
Формулы Коши и Лагранжа
Теорема. Пусть функции  и
и 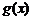
а) определены и непрерывны на 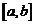 ;
;
б) 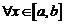
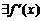 и
и 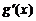 ;
;
в) 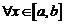
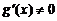 .
.
Тогда существует точка 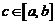 такая, что
такая, что
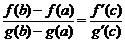 .
.
Эта формула носит название формулы Коши.
Доказательство. Прежде всего отметим, что 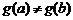 , иначе, по теореме Ролля, существовала бы точка
, иначе, по теореме Ролля, существовала бы точка 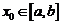 , где
, где 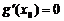 , что противоречит ограничению «в».
, что противоречит ограничению «в».
Рассмотрим функцию
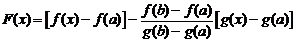 .
.
Она
а) определена и непрерывна на 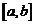 , так как
, так как 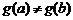 и функции
и функции  и
и 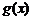 непрерывны на
непрерывны на 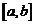 ;
;
б) 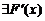
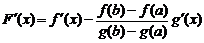 .
.
в) 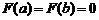 .
.
Таким образом, для 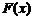 выполнены все условия теоремы Ролля. Поэтому
выполнены все условия теоремы Ролля. Поэтому 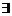
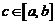 такая, что
такая, что
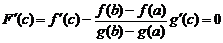 ,
,
но тогда в этой точке 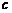
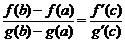 ,
,
что и дает формулу Коши. <
Формула Лагранжа
Рассмотри частный случай, когда 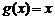 . Тогда формула Коши приобретает вид
. Тогда формула Коши приобретает вид
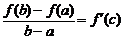 ,
,
или
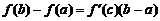 ,
,
где 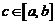 . Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
. Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
Заметим, что точка 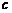 не обязательно единственная: может быть несколько точек
не обязательно единственная: может быть несколько точек 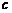 , удовлетворяющих формулам Коши или Лагранжа.
, удовлетворяющих формулам Коши или Лагранжа.
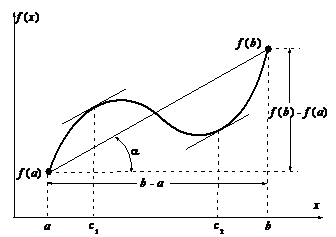 | Рассмотрим еще вопрос о геометрическом смысле формулы Лагранжа. Пусть мы имеем график  . Проведем через точки . Проведем через точки 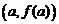 и и 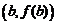 секущую. Она образует с осью OX угол секущую. Она образует с осью OX угол 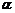 и, как видно из рисунка, и, как видно из рисунка, 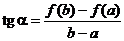 . Но . Но 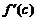 есть тангенс угла, который касательная к кривой в точке есть тангенс угла, который касательная к кривой в точке 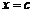 образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка 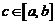 , , |
в которой касательная параллельна секущей, соединяющей точки 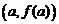 и
и 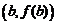 .
.
Дифференциал
Рассмотрим важное для дальнейшего понятие дифференциала.
Напомним, что величина 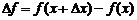 называется приращением функции.
называется приращением функции.
Определение 1. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 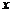 , если ее приращение можно представить в виде
, если ее приращение можно представить в виде
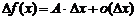 .
.
Определение 2. Линейная часть приращения функции, то есть 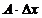 называется дифференциалом функции
называется дифференциалом функции  и обозначается
и обозначается 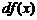
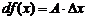 .
.
Чтобы точно уяснить эти определения функции рассмотрим пример. Пусть 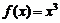 . Тогда
. Тогда
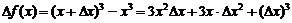
Заметим, что 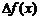 содержит слагаемое, линейное по
содержит слагаемое, линейное по 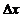 , слагаемые с
, слагаемые с 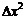 и
и 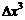 . Так вот, только слагаемое, линейное по
. Так вот, только слагаемое, линейное по 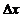 дает дифференциал, то есть
дает дифференциал, то есть
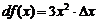 .
.
Выражение для дифференциала
Итак, мы получили, что для дифференцируемой функции 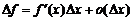 . Это означает, что
. Это означает, что
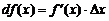 .
.
Но если взять 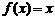 , то мы получим, что
, то мы получим, что 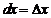 , то есть дифференциал независимой переменной равен ее приращению. Поэтому окончательно
, то есть дифференциал независимой переменной равен ее приращению. Поэтому окончательно
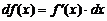
Отсюда следует, что
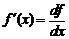
то есть производная есть отношение дифференциала функции к дифференциалу независимой переменной. Заметьте, что 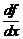 есть обычная дробь и с ней можно обращаться как с обычной дробью.
есть обычная дробь и с ней можно обращаться как с обычной дробью.
Правила дифференцирования
Пользуясь формулой 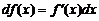 выведем несколько важных формул, касающихся дифференциалов.
выведем несколько важных формул, касающихся дифференциалов.
1. 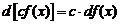 .
.
Действительно
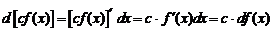 .
.
2. 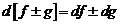
Имеем
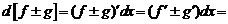
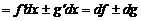 .
.
3. 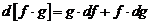 .
.
Имеем
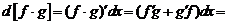
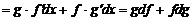 .
.
4. 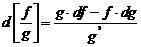 .
.
Имеем
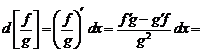
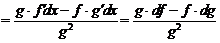 .
.
5. 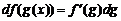 .
.
Имеем
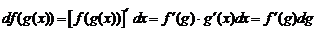 .
.
В качестве приложения понятия дифференциала выведем формулу для производной от функций, заданных параметрически.
Параметрическое задание функции заключается в том, что и 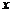 и
и 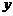 задаются как функции некоторого параметра
задаются как функции некоторого параметра 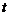 , то есть
, то есть
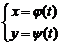 ,
, 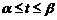 .
.
Значение параметра 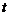 определяет одновременно и
определяет одновременно и 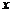 и
и 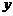 , и, тем самым, некоторую точку на плоскости. Меняя
, и, тем самым, некоторую точку на плоскости. Меняя 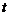 , мы двигаем точку на плоскости, и она описывает некоторую кривую, определяющую зависимость
, мы двигаем точку на плоскости, и она описывает некоторую кривую, определяющую зависимость 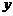 от
от 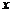 . Параметрическое задание функции считается самым общим способом задания кривых на плоскости.
. Параметрическое задание функции считается самым общим способом задания кривых на плоскости.
Имеем
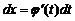 ,
,
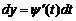 .
.
Отсюда производная от 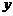 по
по 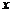 имеет вид
имеет вид

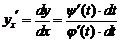 .
.
Сокращая на 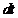 получим окончательно
получим окончательно
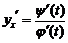 .
.
Формула Тейлора.
Свойства остаточного члена.
Напишем 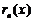 в явном виде
в явном виде
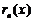 =
= 
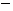
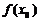
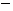
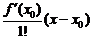
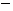
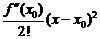
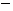

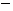
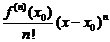 .
.
Полагая 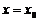 , получим
, получим
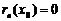
Далее, находя производные и полагая 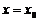 , получим
, получим
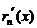 =
= 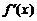
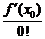
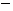
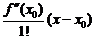

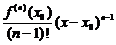 ,
,
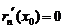 ,
,
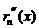 =
= 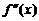
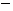
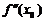
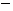

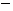
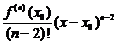 ,
,
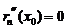 ,
,






























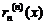 =
= 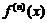
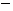
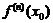 ,
,
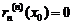 .
.
Таким образом, остаточный член в формуле Тейлора обладает следующим основным свойством

