Доказательство ограниченности последовательности.
Итак, пусть 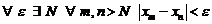 . Зафиксируем
. Зафиксируем 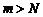 . Тогда
. Тогда 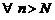
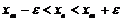 .
.
Рассмотрим
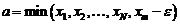 ,
,
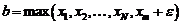 .
.
Тогда очевидно, что 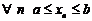 и последовательность
и последовательность 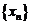 ограниченна.
ограниченна.
2. Выделение сходящейся подпоследовательности
Ссылаясь на лемму Больцано-Вейерштрасса выделим из нашей последовательности подпоследовательность 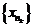 которая сходится к конечному пределу
которая сходится к конечному пределу 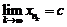 .
.
3. Доказательство того, что вся последовательность сходится к тому же пределу
Так как 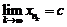 , то
, то 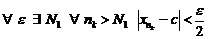 .
.
По условию леммы 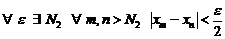 .
.
Возьмем 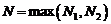 . Тогда
. Тогда 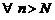 , взяв произвольное
, взяв произвольное 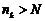 , получим
, получим
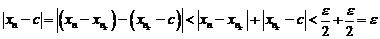 ,
,
что и говорит о том, что 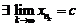 . <
. <
Признак Больцано-Коши имеет более теоретическое, чем практическое значение. Однако на его основе строится целый ряд рабочих признаков сходимости для целого ряда математических объектов.
2.10 Функция и способы ее задания
Пусть имеются две вещественные оси 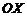 и
и 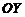 . Пусть на оси
. Пусть на оси 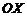 выбрано некоторое множество
выбрано некоторое множество 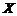 . Правило, которое каждому значению
. Правило, которое каждому значению 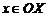 ставит в соответствие некоторое число
ставит в соответствие некоторое число 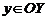 , называется функцией одной переменной и обозначается
, называется функцией одной переменной и обозначается 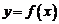 .
.
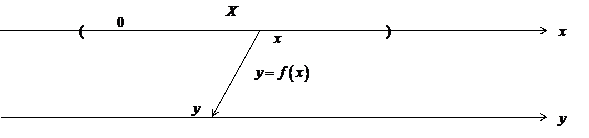
Множество 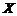 , где такое определение имеет смысл, называется областью определения функции. Однако, при доказательстве различных теорем в качестве множества
, где такое определение имеет смысл, называется областью определения функции. Однако, при доказательстве различных теорем в качестве множества 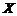 мы будем брать только какую-то часть области определения. Эту часть мы будем называть областью задания функции.
мы будем брать только какую-то часть области определения. Эту часть мы будем называть областью задания функции.
Способы задания функции.
1. Аналитический способ.
В этом случае функция 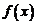 задается в виде одной или нескольких формул, описывающих правило, устанавливающее соответствие
задается в виде одной или нескольких формул, описывающих правило, устанавливающее соответствие 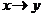 . Например
. Например
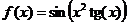 ,
,
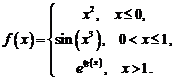
2. Графический способ.
 | В этом случае оси 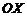 и и 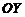 располагаются перпендикулярно друг другу так, что они образуют декартову систему координат. Соответствие располагаются перпендикулярно друг другу так, что они образуют декартову систему координат. Соответствие 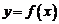 для каждого для каждого 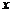 определяет некоторую точку на плоскости определяет некоторую точку на плоскости 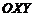 . Совокупность этих точек образует некоторую кривую на плоскости . Совокупность этих точек образует некоторую кривую на плоскости 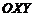 , которая называется графиком функции. Если нарисован график функции, то тем самым задано и правило, определяющее соответствие , которая называется графиком функции. Если нарисован график функции, то тем самым задано и правило, определяющее соответствие 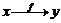 . . |
3. Табличный способ.
| В этом случае функция задается в виде таблицы, в одном из столбцов которой перечислены значения аргумента 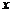 , а в другом указаны соответствующие значения , а в другом указаны соответствующие значения 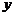 . Конечно, в одной таблице перечислить все значения аргумента . Конечно, в одной таблице перечислить все значения аргумента 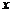 невозможно, но какое-то представление о виде соответствия невозможно, но какое-то представление о виде соответствия 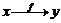 такая таблица обычно дает. такая таблица обычно дает. |
4. Алгоритмический способ.
В этом случае соответствие 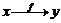 задается в виде некоторого алгоритма, позволяющего находить
задается в виде некоторого алгоритма, позволяющего находить 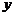 по
по 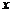 .
.
Например:
а) выписать 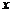 в виде бесконечной десятичной дроби. Например
в виде бесконечной десятичной дроби. Например 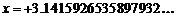 ;
;
б) выписать без изменения знак 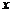 и те цифры которые стоят до запятой;
и те цифры которые стоят до запятой;
в) после запятой выписать первую, третью, пятую и так далее, т.е. вообще цифры с нечетными порядковыми номерами.
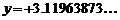
Это и определит значение 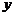 . Вряд ли это правило может быть легко записано в виде формул.
. Вряд ли это правило может быть легко записано в виде формул.
2.11 Предел функции.
Определение. Число b называется пределом или предельным значением функции 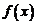 при
при 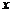 стремящимся к
стремящимся к 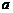 (обозначение:
(обозначение: 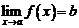 ,
, 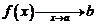 ) если
) если
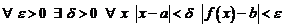 .
.
Это понятие предела также связано с идеей движения. В этом случае движение отражается в том, что при изменении аргумента x изменяется значение функции. Понятие предела возникает при определенном типе такого движения - когда аргумент приближается к a, то значения функции приближается к b.
Приведем без комментариев некоторые варианты этого определения
а) 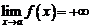 это значит, что
это значит, что
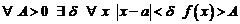 ;
;
б) 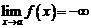 это значит, что
это значит, что
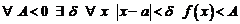 ;
;
в) 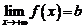 это значит, что
это значит, что
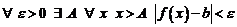 ;
;
г) 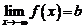 это значит, что
это значит, что
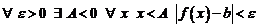 ;
;
д) 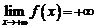 это значит, что
это значит, что
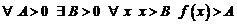 .
.
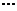
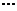
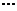
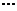
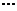
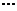
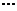
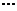
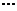
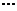
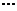
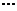
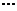
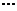
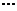
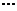
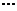
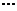
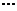
Вариантом этого определения являются так называемые односторонние пределы.
Определение. Число b называется пределом или предельным значением 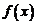 при
при 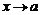 справа (обозначение
справа (обозначение 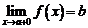 ) если
) если
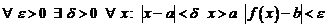 .
.
Число b называется пределом или предельным значением 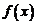 при
при 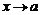 слева (обозначение
слева (обозначение 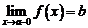 ) если
) если
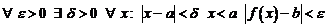 .
.
Напишите сами определение 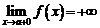 и
и 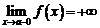 .
.
