Использование дифференциала для приближенных вычислений

Перепишем формулу (3.13), заменив в ней главную часть приращения функции дифференциалом

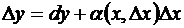. (3.21)

Из полученного выражения следует, что хотя дифференциал dy функции 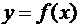не равен приращению Dy этой функции, но, так как 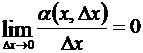, то с точностью до бесконечно малой более высокого порядка, чем Dх, справедливо приближенное равенство

Dy » dy.(3.22)

Относительная погрешность этого равенства становится сколь угодно малой при достаточно малом Dх.

Выгода замены приращения функции Dу ее дифференциалом dy состоит в том, что dy зависит от Dх линейно, в то время как Dу представляет собой обыкновенно более сложную функцию от Dх.

Если положить Dх = х – х₀ и х₀ + Dх = х, то равенство (3.22) принимает вид: f (x) – f (x₀) » 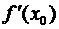(x – x₀) или

f (x) = f (x₀) + 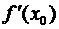(x – x₀). (3.23)

Формула (3.23) определяет способ приближенного вычисления функции. По этой формуле для значений х, близких к х₀, функция f(x) приближенно заменяется линейной функцией. Геометрически это соответствует замене участка кривой y = f(x), примыкающего к точке (х₀, f(x₀)), отрезком касательной к кривой в этой точке (см. формулу (3.3)).

В частности, взяв для простоты х₀ = 0 и ограничиваясь малыми значениями х, будем иметь приближенную формулу:

f (x) » f (0) + 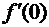x.(3.24)

Отсюда, подставляя вместо f(x) различные элементарные функции, легко получить ряд приближенных формул:

(1+x)^m = 1+mx; sin x » x; tg x» x; e^x»1+x; ln(1+x) » x и т.п.

§3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

ЧИСЛОВОЙ ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО

3.1. Определение производной n-го порядка

Как уже отмечалось в §1, п.1.1, производная 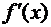функции y = f(x), определенной и дифференцируемой на некотором промежутке Р представляет собой функцию, также определенную на промежутке Р. Может случиться, что эта функция 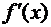сама является дифференцируемой в некоторой точке х промежутка Р, т.е. имеет в этой точке производную. Тогда указанную производную называют второй производной (или производной второго порядка) функции у = f(x) в упомянутой точке х, и обозначают одним из символов

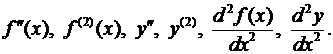
После того как введено понятие второй производной, можно последовательно ввести понятие третьей производной, затем четвертой производной и т.д. Если предположить, что нами уже введено понятие (n – 1)-й производной и что (n – 1)-я производная дифференцируемая в некоторой точке х промежутка Р, т.е. имеет в этой точке производную, то указанную производную называют n-й производной (или производной n-го порядка) функции у = f(x) в точке х и для обозначения ее применяются символы:

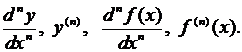
Соотношение, определяющее n-ю производную, имеет вид

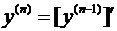. (3.25)

Функцию, имеющую на данном промежутке Р конечную производную порядка n, обычно называют n раз дифференцируемой на данном промежутке.

3.2. Вычисление производной n-го порядка

Методика вычисления производных высшего порядка предполагает умение вычислять только производные первого порядка. Поэтому для того чтобы вычислить n-ю производную от какой-либо функции, нужно предварительно вычислить производные всех предшествующих порядков. В качестве примеров вычислим производные n-го порядка некоторых элементарных функций.

1) Рассмотрим сначала степенную функцию 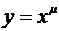(х > 0, μÎR). Последовательно дифференцируя, будем иметь

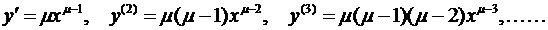
Отсюда легко уяснить общий закон

.

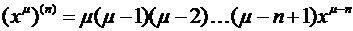Если, например, взять μ = –1, то получим

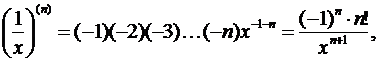
а при 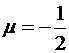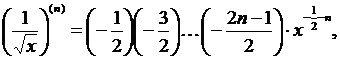и т.п.

2) Пусть теперь Прежде всего имеем

Возьмем отсюда производную (n – 1)-го порядка по соответствующей формуле из 1), заменив в ней n на n – 1; мы и получим тогда

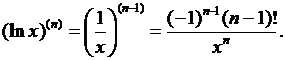
3) Если у = а^х (0 < а ¹ 1), то .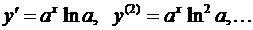

Общая формула, легко устанавливая по методу индукции, имеет вид

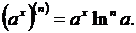
4) Положим 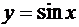; тогда 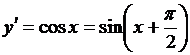. Таким образом, дифференцирование функции 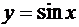прибавляет к аргументу этой функции величину. 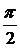Отсюда получаем формулу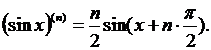

5) Аналогично устанавливается и формула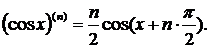

3.3. Формула Лейбница для n-й производной произведения двух функций

В то время как установленное в §1, п.1.4 правило вычисления первой производной от суммы или разности двух функций 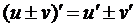легко переносится (например, последовательным применением этих правил) на случай n-й производной (u ± v)⁽ⁿ⁾ = u⁽ⁿ⁾ ± v⁽ⁿ⁾, возникают большие затруднения при вычислении n-й производной от произведения двух функций .

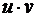Соответствующее правило носит название формулы Лейбница, и имеет следующий вид:

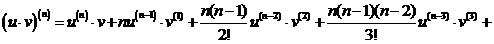
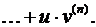(3.26)

Примеры. Вычислить n-ю производную функций:

1. у = х²cos x. Воспользуемся формулой Лейбница, положив в ней 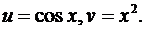В таком случае для любого номера к 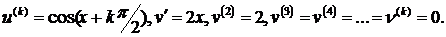Следовательно,

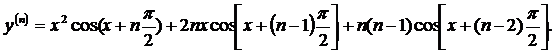
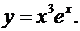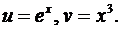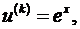
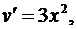
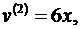
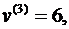
2. Положим Тогда 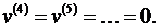Таким образом,

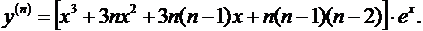
Рассмотренные примеры показывают, что формула Лейбница особенно эффективна в случае, когда одна из двух перемножаемых функций имеет лишь конечное число отличных от нуля производных.