Глава 6. Пределы и непрерывность
Краткая теория
1. Если по некоторому закону каждому натуральному числу п поставлено в соответствие определенное число ап, то говорят, что задана числовая последовательность {ап}.
2. Число А называется пределом числовой последовательности {ап}, если для любого e > 0 найдется такой номер N, зависящий от e, что для всех членов последовательности с номерами п > N верно неравенство 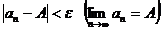 .
.
3. Число А называется пределом функции у = f(х) при х ® ¥, если для любого
e > 0 найдется также число S > 0, зависящее от e, что для всех х таких, что |х| > S будет верно неравенство  .
.
4. Число А называется пределом функции f(х) при х ® x0 , если для любого e > 0 найдется число d > 0, зависящее от e, что для все х ≠ x0 и удовлетворяющих условию
|x – x0| < d выполняется неравенство 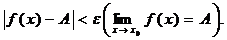
5. Функция a(х) называется бесконечно малой величиной при х ® x0 (или
х ® ¥), если 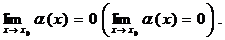
6. Функция f(x) называется бесконечно большой величиной при х ® x0 , если для любого М > 0 найдется такое число d > 0, зависящее от М, что для всех х ≠ x0 и удовлетворяющих условию |x – x0| < d будет верно неравенство 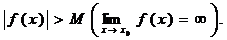
7. Свойства бесконечно малых. Если a(х) и b(х) — бесконечно малые величины при х ® x0 (или х ® ¥), то будут бесконечно малыми величины: a(х) ± b(х); с × a(х),
с – постоянная; f(x)× a(х) (f(x) – ограниченная функция); a(х) × b(х); 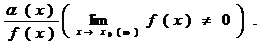
8. Свойства бесконечно больших. Если f(x) и j(х) – бесконечно большие величины при х ® x0 (или х ® ¥), то будут бесконечно большими величинами: 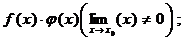
 f(x) + j(х) (j(х) — ограниченная функция); f(x)/j(х) (j(х) имеет предел).
f(x) + j(х) (j(х) — ограниченная функция); f(x)/j(х) (j(х) имеет предел).
9. Если функция a(х) есть бесконечно малая величина при х ® x0 (или х ® ¥), то функция 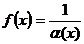 является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х ® x0 (х ® ¥) , то
является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х ® x0 (х ® ¥) , то 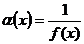 является бесконечно малой величиной.
является бесконечно малой величиной.
10. Сравнение порядков бесконечно малых. Если a(х) и b(х) — бесконечно малые величины при х ® x0 (х ® ¥) и 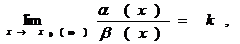 то при k = 0 бесконечно малая a(х) называется бесконечно малой более высокого порядка малости, чем b(х); при 0 < k < ¥ — одного порядка малости; при k = ¥ — более низкого порядка малости, чем b(х).
то при k = 0 бесконечно малая a(х) называется бесконечно малой более высокого порядка малости, чем b(х); при 0 < k < ¥ — одного порядка малости; при k = ¥ — более низкого порядка малости, чем b(х).
 Если k = 1, то бесконечно малые a(х) и b(х) называются эквивалентными: a(х) ~b(х).
Если k = 1, то бесконечно малые a(х) и b(х) называются эквивалентными: a(х) ~b(х).
11. Примеры эквивалентных бесконечно малых величин при х ® 0: sin x ~ x; ln(1+x) ~ x; (1 + x) m ~ 1+ mx; arcsin x ~ x; arctg x ~ x; 1 – cos x ~ x2/2.
12. Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые заменить им эквивалентными.
13. Теоремы о пределах:
1) 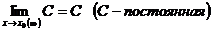 .
.
2) Если 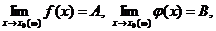
то: 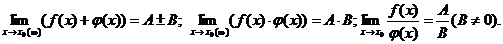
14. Если 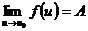 ,
, 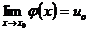 , то
, то 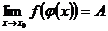 .
.
15. Первый замечательный предел: 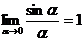
16. Второй замечательный предел (число е): 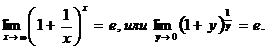
6.1. Определение предела. Простейшие пределы
Для того чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
6.4. Найти 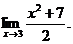
Решение. Подставляем вместо х в выражение под знаком предела 3, получим
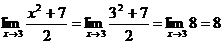 .
.
6.5. Найти 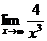 .
.
Решение. Знаменатель дроби х3 при х ® ¥ является бесконечно большой величиной, 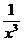 при х ® ¥ является бесконечно малой величиной, следовательно, искомый предел равен нулю.
при х ® ¥ является бесконечно малой величиной, следовательно, искомый предел равен нулю.
6.6. Найти 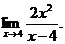
Решение. Знаменатель дроби (х — 4) при х ® 4 является бесконечно малой величиной, тогда 1/(х – 4) – бесконечно большая величина; числитель дроби 2х2 является функцией, предел которой отличен от нуля 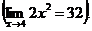
Функция 2х2/(х – 4) является бесконечно большой величиной, т.е. искомый предел равен ¥.
6.2. Раскрытие неопределенностей различных типов
Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов
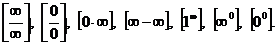
Устранить неопределенность удается часто с помощью алгебраических преобразований.
6.12. Найти 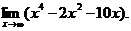
Решение. Имеем неопределенность вида [¥ – ¥]. Вынесем за скобку х в наибольшей степени: 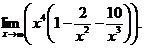
х4 является бесконечно большой величиной при х ® ¥. По теоремам о пределах
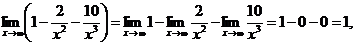
так как 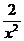 и
и 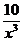 при х ® ¥ являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно больших
при х ® ¥ являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно больших 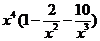 является бесконечно большой величиной, т.е. искомый предел равен ¥.
является бесконечно большой величиной, т.е. искомый предел равен ¥.
Ответ данной задачи и приведенные в решении выкладки будем использовать при решении следующих примеров как заранее известные факты. Рассмотрим несколько типов примеров, классифицируя их по виду неопределенности и предельному значению х.
1-й тип. Рассмотрим примеры вида 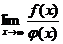 с неопределенностью вида
с неопределенностью вида 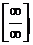 , где f(x) и j(х) в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
, где f(x) и j(х) в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
6.13. Найти 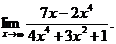
Решение. 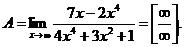 Вынося за скобку и в числителе и в знаменателе х в наибольшей степени, получим
Вынося за скобку и в числителе и в знаменателе х в наибольшей степени, получим
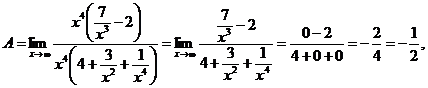
так как 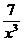 ,
, 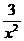 ,
, 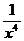 , – величины бесконечно малые при х ® ¥.
, – величины бесконечно малые при х ® ¥.
6.17.Найти 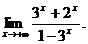
Решение. При 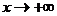 показательная функция
показательная функция 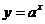 , при
, при 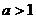 стремится к
стремится к 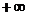 . Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки
. Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки 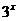 :
:
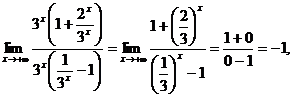
так как при 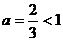
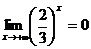 и при
и при 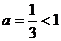
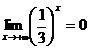 .
.
Найти пределы:
6.18. 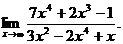
6.19. 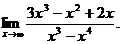
6.20. 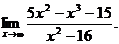
6.21. 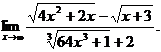
6.22. 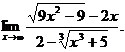
6.23. 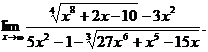
6.24. 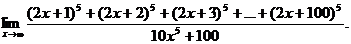
6.25. 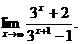
6.26. 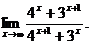
2-й тип.Рассмотрим примеры вида 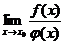 с неопределенностью вида
с неопределенностью вида  В этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
В этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
6.45. Найти 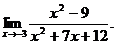
Решение. Имеем неопределенность вида 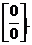 Разложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умножения
Разложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умножения 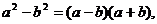 а знаменатель – по формуле разложения квадратного трехчлена на множители при
а знаменатель – по формуле разложения квадратного трехчлена на множители при 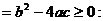
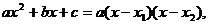 где
где 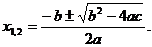
Получим 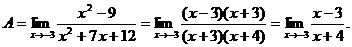
После сокращения дроби следует подставить предельное значение х в сокращенную дробь. Получим 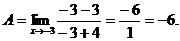
6.46. Найти 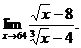
Решение. 1-й способ. Имеем неопределенность вида 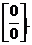 Дополним числитель до разности квадратов
Дополним числитель до разности квадратов 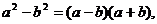 а знаменатель до разности кубов
а знаменатель до разности кубов 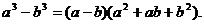 Получим
Получим 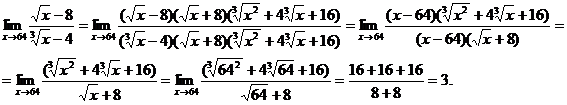
2-й способ. Сделаем замену переменной: 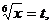 тогда
тогда 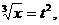 а
а 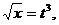 при
при 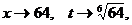 т.е.
т.е. 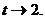 Теперь
Теперь
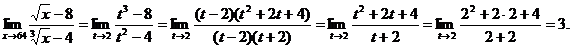
Найти пределы:
6.47. 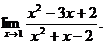
6.48. 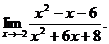
6.49. 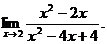
6.50. 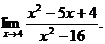
6.51. 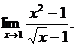
6.52. 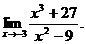
6.53. 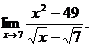
6.54. 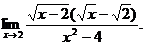
6.55. 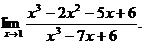
6.56. 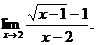
6.57. 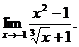
6.58. 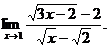
3-й тип.Рассмотрим примеры с неопределенностью вида [∞ – ∞]. Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к 1-му типу путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения.
6.68. Найти 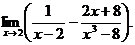
Решение. Имеем неопределенность вида [∞ – ∞]. Приведем дроби к общему знаменателю:
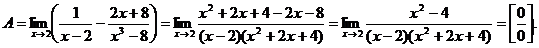
Имеем предел 2-го типа, необходимо разложить на множители числитель дроби. Получим
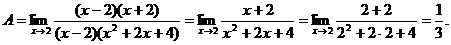
6.69. Найти 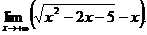
Решение. Имеем неопределенность вида [∞ – ∞]. Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:
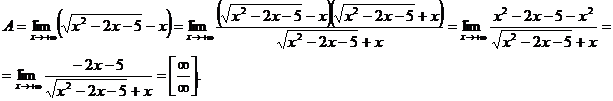
Имеем предел 1-го типа.
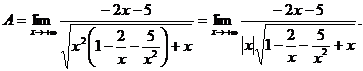
При 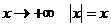 по определению модуля; поэтому
по определению модуля; поэтому
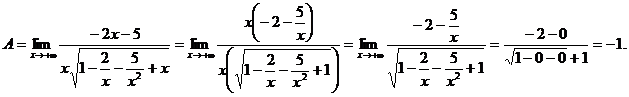
так как при 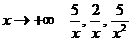 - бесконечно малые величины.
- бесконечно малые величины.
Найти пределы:
6.70. 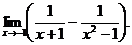
6.71. 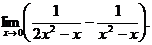
6.72. 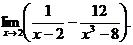
6.73. 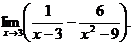
6.74. 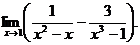
6.75. 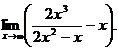
6.76. 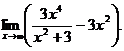
6.77. 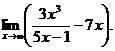
6.78. 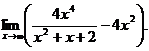
6.79. 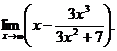
6.80. 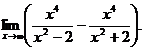
6.81. 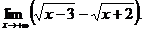
6.82. 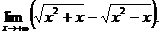
6.83. 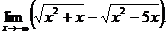
6.84. 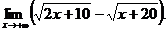
6.85. 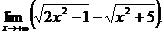
6.86. 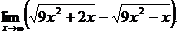
6.87. 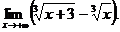
6.3. Замечательные пределы
К пределам 4-го типа отнесем примеры с неопределенностью вида 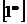 . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .
. В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .
6.97. Найти 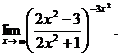
Решение. Имеем неопределенность вида 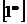 , так как
, так как
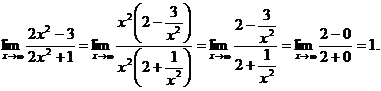
Выделим целую часть дроби 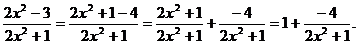
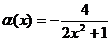 является бесконечно малой величиной при х → ∞. Домножим показатель степени на
является бесконечно малой величиной при х → ∞. Домножим показатель степени на 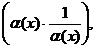 это действие не нарушает знака равенства:
это действие не нарушает знака равенства:
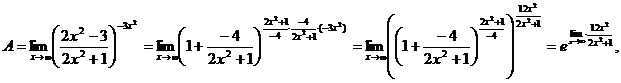
ибо 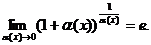 Найдем
Найдем 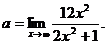 Имеем неопределенность вида
Имеем неопределенность вида 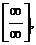 предел 1-го типа. Вынесем за скобки х2, так как вторая степень наибольшая:
предел 1-го типа. Вынесем за скобки х2, так как вторая степень наибольшая:
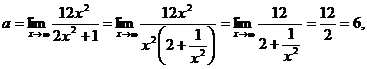
так как 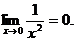 Таким образом предел равен
Таким образом предел равен 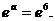
6.99. Найти 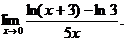
Решение. Имеем неопределенность вида 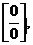 преобразуем ее в неопределенность вида
преобразуем ее в неопределенность вида 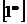 , пользуясь свойствами логарифмов:
, пользуясь свойствами логарифмов:
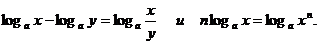
Получим 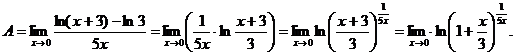
Учитывая непрерывность логарифмической функции, символы lim и ln можно переставить , получим
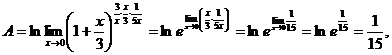
так как по формуле 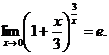
Найти пределы:
6.100. 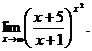
6.101. 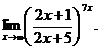
6.102. 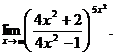
6.103. 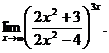
6.104. 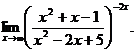
6.105. 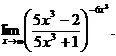
6.106. 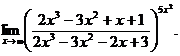
6.107. 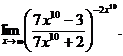
6.108. 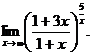
5-й тип. К этому типу отнесем функции, сводящиеся к первому замечательному пределу (6.1): 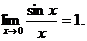
6.121. Найти 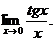
Решение. 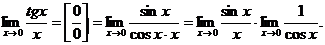
Первый сомножитель представляет собой первый замечательный предел и равен 1, второй сомножитель представляет предел, равный 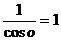 . Таким образом, искомый предел равен 1×1 = 1.
. Таким образом, искомый предел равен 1×1 = 1.
6.122. Найти 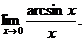
Решение. Имеем неопределенность вида 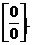 Сделаем замену переменной:
Сделаем замену переменной:
arcsin х = у; тогда х = sin у; при х → 0, у →0; получим 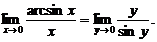
Имеем первый замечательный предел, следовательно искомый предел равен 1, что и требовалось доказать.
Найти пределы:
6.124. 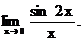
6.125. 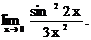
6.126. 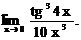
6.127. 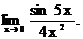
6.128. 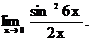
6.129. 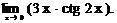
6.130. 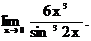
6.131. 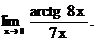
6.132. 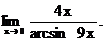
6.133. 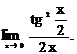
6.134. 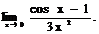
6.135. 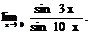
He рассмотренные в этой главе неопределенности видов [0×¥], [0°] и [¥°] могут быть устранены при помощи правила Лопиталя, которое будет рассмотрено в главе 8.
6.5. Непрерывность функции и точки разрыва.
Краткая теория
1. Функция 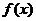 называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х→ x0;
называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х→ x0;
3) этот предел равен значению функции в этой точке: 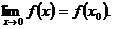 (6.1)
(6.1)
(первое определение).
2.Функция 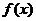 называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 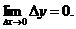 (6.2)
(6.2)
(второе определение).
3.Если функции 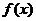 и
и 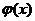 непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
4. Если функция у = 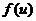 непрерывна в точке u0 =
непрерывна в точке u0 = 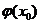 , а функция u=
, а функция u= 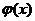 непрерывна в точке x0, то сложная функция у =
непрерывна в точке x0, то сложная функция у = 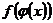 непрерывна в точке x0.
непрерывна в точке x0.
5. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны во всех точках, где они определены.
6. Если не выполнено определение непрерывности (6.1) или (6.2), то функция в точке x0 терпит разрыв, причем:
а) если хотя бы один из односторонних пределов 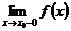 или
или 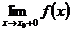
бесконечен, то x0 - точка разрыва второго рода;
б) если оба односторонних предела 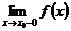 и
и 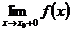 конечны, но не равны между собой, то x0 — точка неустранимого разрыва первого рода;
конечны, но не равны между собой, то x0 — точка неустранимого разрыва первого рода;
в) если оба односторонних предела 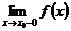 и
и 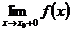 конечны, равны между собой, но не равны
конечны, равны между собой, но не равны 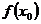 , то x0 — точка устранимого разрыва первого рода.
, то x0 — точка устранимого разрыва первого рода.
6.168.Исследовать на непрерывность функции у = 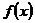 в точке х = 1. В случае разрыва установить его характер в точке х = 1:
в точке х = 1. В случае разрыва установить его характер в точке х = 1:
а) 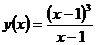 ; б)
; б) 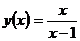 ; в)
; в) 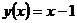 ; г)
; г) 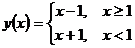 .
.
Решение: а) При х = 1 функция не определена, следовательно, функция в точке
х = 1 терпит разрыв (рис. 6.1): 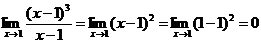 , т.е. конечный предел существует; следовательно, х = 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точке х = 1, т.е. положив
, т.е. конечный предел существует; следовательно, х = 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точке х = 1, т.е. положив 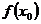 = 0, получим, что новая функция
= 0, получим, что новая функция
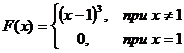 будет уже непрерывна в точке х = 1 .)
будет уже непрерывна в точке х = 1 .)
6) При x = 1 функция не определена, следовательно, функция в точке x = 1 терпит разрыв (рис. 6.2): 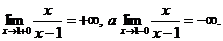
Так как односторонние пределы (достаточно было бы одного) бесконечны, то х = 1 – точка разрыва функции второго рода.
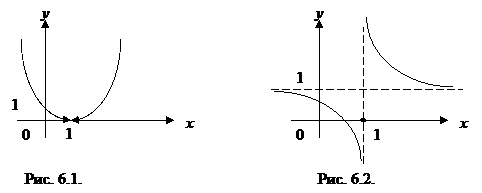 |

в) При х = 1 функция определена, 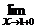 (x-1) = 0,
(x-1) = 0, 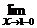 (x-1) = 0,у (1) = 1 - 1 = 0, т.е.
(x-1) = 0,у (1) = 1 - 1 = 0, т.е. 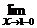 у(х)=
у(х)= 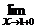 у(х) = у(1) = 0, следовательно, функция в точке х = 1 непрерывна
у(х) = у(1) = 0, следовательно, функция в точке х = 1 непрерывна
(рис. 6.3).
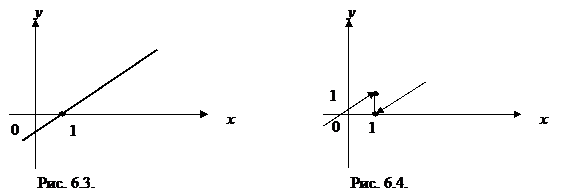 |
г) При х = 1 функция определена, у(1)=0,
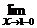 у(х)=
у(х)= 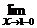 (х+1)=2,
(х+1)=2, 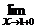 у(х)=
у(х)= 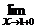 (х-1)=0,
(х-1)=0,
 имеем
имеем 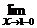 у(х) ≠
у(х) ≠ 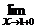 у(х), таким образом, в точке х = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)
у(х), таким образом, в точке х = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)
Глава 7. Производная
7.1. Определение производной
Краткая теория
1. Производной функции 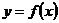 называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):
называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):
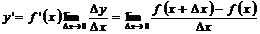 . (7.1)
. (7.1)
Если функция в точке 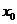 (или на промежутке
(или на промежутке 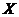 ) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке
) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке 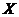 ).
).
2. Если функция 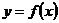 дифференцируема в точке
дифференцируема в точке 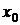 , (или на промежутке
, (или на промежутке 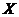 ), то она в этой точке непрерывна (или на промежутке
), то она в этой точке непрерывна (или на промежутке 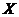 ). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.
). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.
1.Используя определение производной, найти производную функции 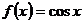 .
.
Решение. Придавая аргументу 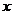 приращение
приращение 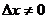 , найдем соответствующее приращение функции:
, найдем соответствующее приращение функции:
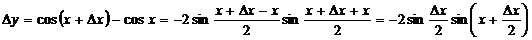 .
.
Составим отношение:
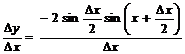 .
.
Найдем предел этого отношения при 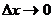 :
:
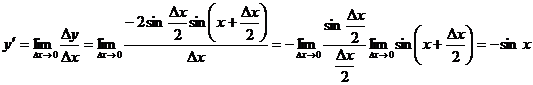
(ибо в силу (6.1) первый предел равен 1).
Таким образом: 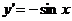 .
.
2. Доказать, что функция 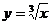 непрерывна, но не дифференцируема в точке
непрерывна, но не дифференцируема в точке 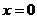 .
.
Решение.Функция: 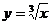
1) определена на всей числовой оси, в том числе в точке 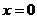 ;
;
2) существует конечный предел 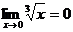 ;
;
3) этот предел равен значению функции в точке 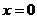 , т.е.
, т.е. 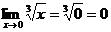 .
.
Таким образом, согласно определению (6.4) непрерывности функции в точке, функция непрерывна при 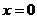 .
.
Производная функции
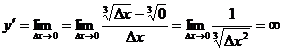 ,
,
т.е. функция не является дифференцируемой при 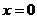 .
.
Используя определение производной, найти производные функций:
1. 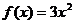 .
.
2. 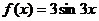 .
.
3. 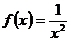 .
.
4. 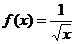 .
.
5. 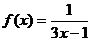 .
.
6. 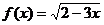 .
.
Доказать, что функции непрерывны и дифференцируемы при 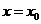 :
:
7. 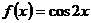 ,
, 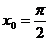 .
.
8. 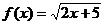 ,
, 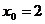 .
.
Доказать, что функции являются непрерывными, но не дифференцируемы при 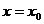 :
:
9. 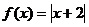 ,
, 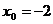 .
.
10. 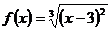 ,
, 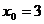 .
.
7.2 Правила дифференцирования. Производные элементарных функций.
Краткая теория
