Практическая работа №6 «Решение задач на законы распределения вероятностей дискретных случайных величин».

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Дискретной назовём случайную величину, возможные значения которой образуют конечное множество.

Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению x_i ставится в соответствие вероятность p_i, с которой случайная величина может принять это значение, причём .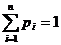

Пример.Абитуриент сдаёт два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины х, числа полученных пятёрок, если вероятность получения пятёрки по математике равна 0,8, а по физике – 0,6.

Решение.Обозначим А₁ и А₂ – события, заключающиеся в том, что и математика, и физика сданы на 5. Очевидно, возможные значения х есть 0, 1, 2, причём

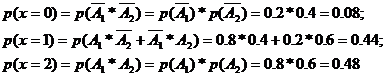
Полученные результаты сведём в таблицу:

xi
pi	0.08	0.44	0.48

.

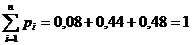Практическая работа №7 «Нахождение числовых характеристик дискретных случайных величин».

К важнейшим числовым характеристикам случайной величины относятся математическое ожидание и дисперсия.

Математическим ожиданием дискретной случайной величины х называется произведение всех её возможных значений на их вероятности:

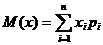
Свойства математического ожидания:

- математическое ожидание постоянной равно самой постоянной:

М(С)=С

- постоянный множитель можно выносить за знак математического ожидания:

М(Сх)=С*М(х)

- математическое ожидание суммы случайных величины равно сумме математических ожиданий слагаемых:

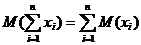
- математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей:

М(х₁*х₂*…*х_n)=М(х₁)*М(х₂)*…М(х_n)

Дисперсией случайной величины х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(x)=M((x-M(x))²) или D(x)=M(x²) – (M(x))²

Среднеквадратическое отклонение: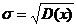

Свойства дисперсии:

- дисперсия постоянной равно нулю:

D(С)=0

- постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(Сх)=С²*D(х)

- дисперсия суммы (разности) случайных величины равно сумме дисперсий слагаемых:

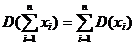
Свойства среднеквадратического отклонения:

-

-

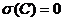
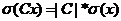
Пример 1.Закон распределения случайной величины задан таблично. Найти р(х<2), р(х>4), р(2≤х≤4), математическое ожидание, дисперсию и среднеквадратическое отклонение.

xi
pi	0,1	0,2	0,4	0,2	0,1

Решение.р(х<2)=0,1;

р(х>4)=0,1;

р(2≤х≤4)=0,2+0,4+0,2=0,8;

М(х)=1*0,1+2*0,2+3*0,4+4*0,2+5*0,1=3;

D(x)=1²*0,1+2²*0,2+3²*0,4+4²*0,2+5²*0,1-3²=1,2

σ(x)= 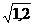=1,095

Пример 2.Фермер считает, что, принимая во внимание различные потери и колебания цен, он сможет выручить не более 60 центов за десяток яиц и потерять не более 20-ти центов за десяток и что вероятности возможных выигрышей и потерь таковы:

цена за 10 яиц	0,6	0,4	0,2		-0,2
Р	0,2	0,5	0,2	0,06	0,04

Как оценить ожидаемую прибыль от продажи десятка яиц; от ожидаемых им в этом году 100000 яиц?

Решение.х – случайная, прибыль от продажи 10 яиц.

М(х)=0,6*0,2+0,4*0,5+0,2*0,2+0*0,06-0,2*0,04=0,352

М(10000х)=10000*0,352=3520 $

D(x)=0.6²*0.2+0.4²*0.5+0.2²*0.2+0²*0.06+(-0.2)²*0.04-0.352²=0.037696

σ(x)= =0.194154578

D(10000x)=10000²* D(x)=19415457.76

σ(x)= 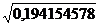=0.441