Разработка pascal-программ для решения трансцендентных уравнений и вычисления определенных интегралов

Задание на учебную практику 11ЭМб

на тему:

РАЗРАБОТКА PASCAL-ПРОГРАММ ДЛЯ РЕШЕНИЯ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ И ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Цель работы

Освоение методов проектирования программ на языке Turbo Pascal для решения трансцендентных уравнений и вычисления определенных интегралов.

Задание на работу

1. Освоить методы решения трансцендентных уравнений.

2. Разработать программу на языке Turbo Pascal для решения заданного уравнения по заданному методу.

3. Освоить методы нахождения определенных интегралов.

4. Разработать программу на языке Turbo Pascal для нахождения определенного интеграла по заданному методу.

Требования к программе

Кроме основной функции (решения поставленной задачи), программа должна обеспечивать:

- вывод сообщений о назначении программы, начале и об успешном или неудачном окончании работы;

- вывод запросов на ввод исходных данных;

- контроль исходных данных и коррекцию ошибочно введенных значений переменных;

- вывод результатов на экран.

Порядок выполнения работы

1. Выполнить постановку задачи.

2. Освоить метод решения уравнения.

3. Для нахождения корней трансцендентных уравнений определить границы интервала, в котором лежит корень, построением графика в Excel.

4. Разработать блок-схему программы (см. Приложение).

5. Подготовить текст программы и отладить программу с использованием среды Turbo Pascal.

Методы решения уравнений

Постановка задачи

Нахождение корней уравнений – одна из древнейших математических проблем, которая часто встречается в различных областях науки и техники.

Рассмотрим общеизвестное квадратное уравнение

ax² + bx + c = 0

Говорят, что значения

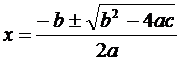
являются корнями этого уравнения, так как для этих значений х уравнение равно 0.

В более общем случае, если имеется некоторая функция F(x), то бывает необходимо найти такие значения аргумента х, для которых

F(x) = 0 (1)

Нелинейные уравнения с одним неизвестным подразделяются на алгебраические, например:

а₀xⁿ + a₁x^n-1 + a₂x^n-2 + … +a_n = 0

и трансцендентные, например:

x –10Sin x = 0

В общем случае функции, которые мы будем рассматривать, не имеют аналитических формул для своих корней, как, например, для квадратного уравнения. Поэтому приходится пользоваться приближенными методами нахождения корней, которые в основном состоят из двух этапов:

1 Отыскание приближенного значения корня (отделение корней);

2 Уточнение приближенного значения до некоторой заданной степени точности.

Отделение корней

Отделение корней – это установление "тесного" промежутка, содержащего только один корень. Отделение корней можно произвести графически. Принимая во внимание, что действительные корни уравнения (1) – это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график F(x) (например, в Excel) и отметить на оси 0х отрезки, содержащие по одному корню.

В сомнительных случаях графическое отделение корней необходимо подтвердить вычислениями. При этом полезно использовать следующие очевидные положения:

1) если непрерывная на отрезке [a, b] функция F(x) принимает на его концах значения разных знаков, т.е. F(a)×F(b) < 0, то уравнение (1) имеет на этом отрезке, по меньшей мере, один корень;

2) если функция F(x) к тому же еще и строго монотонна, то корень на отрезке [a, b] единственный.

Для отделения корней можно эффективно использовать персональный компьютер.

Пусть имеется уравнение F(x) = 0, причем необходимо найти отрезок
[A; B], на котором функция F(x) определена, непрерывна и F(A)×F(B)< 0. Будем вычислять значения F(x) , начиная с точки х = А, двигаясь вправо с некоторым шагом h (рисунок 1). Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция F(x) монотонна на этом отрезке, то соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

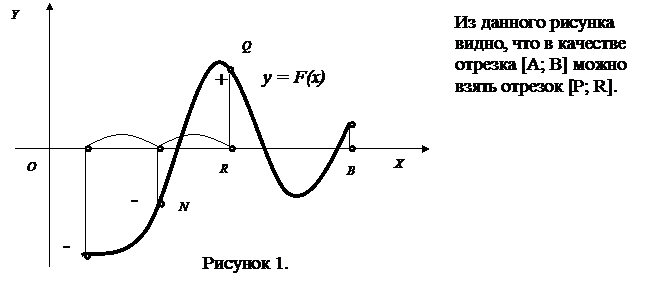h h

A P

M

Блок – схема

Этапа отделения корней

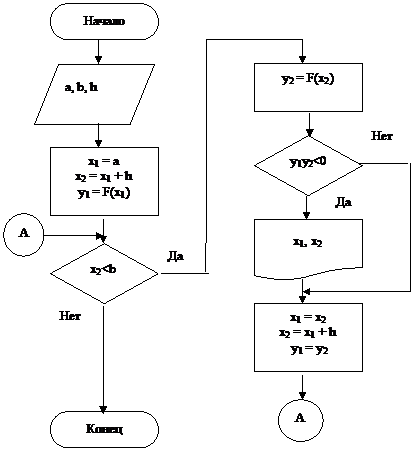Метод простой итерации

Заменим одним из способов, описанных в п. 5.3.1.1, уравнение F(x) = 0 равносильным уравнением x = f(x). Пусть x - корень этого уравнения, а х₀ - полученное каким-либо способом нулевое приближение к корню x. Подставляя х₀ в правую часть нашего уравнения получим некоторое число x₁ = f(x₀). Проделаем то же самое с x₁, получим х₂ = f(x₁) и т.д. Применяя шаг за шагом соотношение x_n = f(x_n-1) для n = 1, 2, …, получим числовую последовательность

x₀, x₁, …, x_n, …,

которую называют последовательностью приближений или итерационной последовательностью (от лат. iteration - повторение).

Последовательность приближений может быть как сходящейся, так и расходящейся. Если последовательность сходится, а функция f(x) непрерывна, то предел последовательности является корнем уравнения x = f(x).

Достаточные условия сходимости итерационного процесса определяются следующей теоремой.

Теорема 1. Пусть уравнение x = f(x) имеет единственный корень на отрезке [a; b] и выполнены условия:

1) f(x) определена и дифференцируема на [a; b];

2) f(x) Î [a; b] для всех х Î [a; b];

3) существует такое вещественное q, что ½f’(x)½£ q <1 для всех х Î [a; b].

Тогда итерационная последовательность x_n = f(x_n-1) (n = 1, 2, …) сходится при любом начальном члене х₀ Î [a; b].

Заметим, что условия теоремы 1 не являются необходимыми, т.е. итерационная последовательность может оказаться сходящейся и при невыполнении этих условий.

Метод прямоугольников

При использовании метода прямоугольников (рис. 1) для вычисления суммы S1 используются формулы:

S1 = h[f(X₁) + f(X₂) + ... f(X_n)],

где X₁ = A + h/2, X₁ = X_i-1 + h.

Метод трапеций

При использовании метода трапеций (рис. 2) для вычисления суммы S₁ используются формулы:

S1 = 0.5 h {f(A) + f(B) + 2[f(X₁) + f(X₂) + ... + f(X_n-1)]},

где X₁ = A + h, X₁ = X_i-1 + h.

6.3 Метод парабол (Симпсона)

При использовании метода Симпсона для вычисления суммы S₁ используется формула:

S1 = 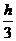{f(A) + f(B) + ... + 2[f(A+h) + f(A+3h) + ... + f(A+(n-1)h] + 4[f(A+2h) + f(A+4h) + ... + f(A+(n-2)h)]},

где n - четное число.

Для вычисления суммы S2 используются те же формулы, только при измененных значениях шага аргумента h и количества интервалов n. 4.

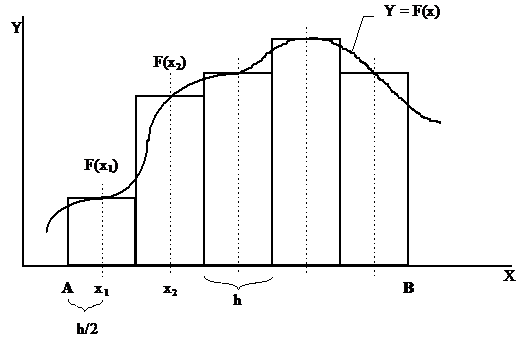
Рисунок 1

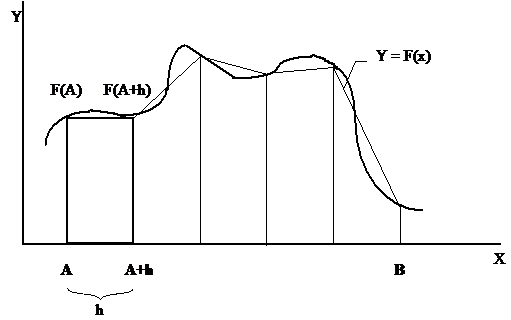
Рисунок 2

Варианты заданий для решения уравнений

№ варианта	Левая часть уравнения	Метод вычислений
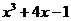		Метод итераций
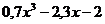		Метод половинного деления
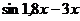		Метод хорд
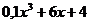		Метод касательных
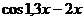		Метод итераций
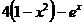		Метод половинного деления
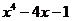		Метод хорд
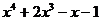		Метод касательных
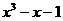		Метод итераций
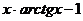		Метод половинного деления
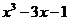		Метод хорд
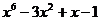		Метод касательных
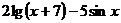		Метод итераций
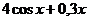		Метод половинного деления
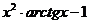		Метод хорд
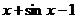		Метод касательных
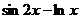		Метод итераций
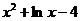		Метод половинного деления
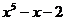		Метод хорд
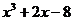		Метод касательных
	x - Sin(x)/2 – 1 = 0	Метод итераций
	2x3 + 4x – 1 = 0	Метод половинного деления
	05x – 8ln(x) - 6 = 0	Метод хорд
	x3 + 12x – 2 =	Метод касательных
	x – Sin(x) = 0.25	Метод итераций

Содержание отчета

· титульный лист;

· содержание;

· задание варианта;

· график заданной функции (функций) в Excel;

· описание заданного численного метода;

· схема программы (блок-схема алгоритма);

· листинг программы на языке Паскаль;

· полученные результаты работы программы;

· выводы.

8 Контрольные вопросы

1. Какое уравнение называется трансцендентным?

2. Какими способами можно определить интервалы корня?

3. В чем суть алгоритма решения уравнений по методу итераций?

4. В чем суть алгоритма решения уравнений по методу хорд?

5. В чем суть алгоритма решения уравнений по методу деления пополам (дихотомии)?

6. В чем суть алгоритма решения уравнений по методу касательных (Ньютона)?

7. Как учитывается абсолютная погрешность при вычислении корня?

8. Контроль каких вводимых данных необходимо осуществлять при решении трансцендентных уравнений?

Задание на учебную практику 11ЭМб

на тему:

РАЗРАБОТКА PASCAL-ПРОГРАММ ДЛЯ РЕШЕНИЯ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ И ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Цель работы

Освоение методов проектирования программ на языке Turbo Pascal для решения трансцендентных уравнений и вычисления определенных интегралов.

Задание на работу

1. Освоить методы решения трансцендентных уравнений.

2. Разработать программу на языке Turbo Pascal для решения заданного уравнения по заданному методу.

3. Освоить методы нахождения определенных интегралов.

4. Разработать программу на языке Turbo Pascal для нахождения определенного интеграла по заданному методу.

Требования к программе

Кроме основной функции (решения поставленной задачи), программа должна обеспечивать:

- вывод сообщений о назначении программы, начале и об успешном или неудачном окончании работы;

- вывод запросов на ввод исходных данных;

- контроль исходных данных и коррекцию ошибочно введенных значений переменных;

- вывод результатов на экран.

Порядок выполнения работы

1. Выполнить постановку задачи.

2. Освоить метод решения уравнения.

3. Для нахождения корней трансцендентных уравнений определить границы интервала, в котором лежит корень, построением графика в Excel.

4. Разработать блок-схему программы (см. Приложение).

5. Подготовить текст программы и отладить программу с использованием среды Turbo Pascal.

Методы решения уравнений

Постановка задачи

Нахождение корней уравнений – одна из древнейших математических проблем, которая часто встречается в различных областях науки и техники.

Рассмотрим общеизвестное квадратное уравнение

ax² + bx + c = 0

Говорят, что значения

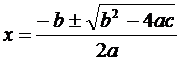
являются корнями этого уравнения, так как для этих значений х уравнение равно 0.

В более общем случае, если имеется некоторая функция F(x), то бывает необходимо найти такие значения аргумента х, для которых

F(x) = 0 (1)

Нелинейные уравнения с одним неизвестным подразделяются на алгебраические, например:

а₀xⁿ + a₁x^n-1 + a₂x^n-2 + … +a_n = 0

и трансцендентные, например:

x –10Sin x = 0

В общем случае функции, которые мы будем рассматривать, не имеют аналитических формул для своих корней, как, например, для квадратного уравнения. Поэтому приходится пользоваться приближенными методами нахождения корней, которые в основном состоят из двух этапов:

1 Отыскание приближенного значения корня (отделение корней);

2 Уточнение приближенного значения до некоторой заданной степени точности.

Отделение корней

Отделение корней – это установление "тесного" промежутка, содержащего только один корень. Отделение корней можно произвести графически. Принимая во внимание, что действительные корни уравнения (1) – это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график F(x) (например, в Excel) и отметить на оси 0х отрезки, содержащие по одному корню.

В сомнительных случаях графическое отделение корней необходимо подтвердить вычислениями. При этом полезно использовать следующие очевидные положения:

1) если непрерывная на отрезке [a, b] функция F(x) принимает на его концах значения разных знаков, т.е. F(a)×F(b) < 0, то уравнение (1) имеет на этом отрезке, по меньшей мере, один корень;

2) если функция F(x) к тому же еще и строго монотонна, то корень на отрезке [a, b] единственный.

Для отделения корней можно эффективно использовать персональный компьютер.

Пусть имеется уравнение F(x) = 0, причем необходимо найти отрезок
[A; B], на котором функция F(x) определена, непрерывна и F(A)×F(B)< 0. Будем вычислять значения F(x) , начиная с точки х = А, двигаясь вправо с некоторым шагом h (рисунок 1). Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция F(x) монотонна на этом отрезке, то соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

h h

A P

M

Блок – схема

Этапа отделения корней