Тема 4.1. Предел числовой последовательности.
Вычислить пределы числовых последовательностей:
1) 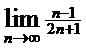 ; 2)
; 2) 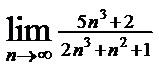 ; 3)
; 3) 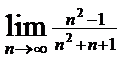 ; 4)
; 4) 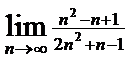 .
.
Тема 4.2. Предел функции. Вычислить пределы функции:
5) 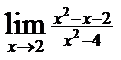 ; 6)
; 6) 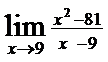 ; 7)
; 7) 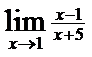 ;8)
;8) 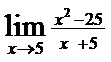 ;
;
9) 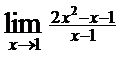 ; 10)
; 10) 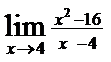 ; 11)
; 11) 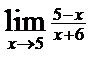 ; 12)
; 12) 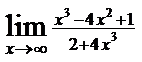 .
.
Тема 5. Производная и её приложения.
Вычислить производную функции : 1) 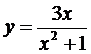 ; 2)
; 2) 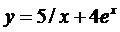 ; 3)
; 3) 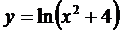 ; 4)
; 4) 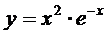 ; 5)
; 5) 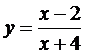 ; 6)
; 6) 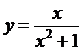 .
.
Вычислить значение производной функции:
1) 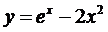 при
при 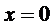 ; 2)
; 2) 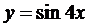 при
при 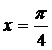 ; 3)
; 3) 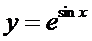 при
при 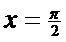 ; 4)
; 4)  при
при 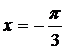 ; 5)
; 5) 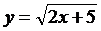 при х = 0,5.
при х = 0,5.
Приложения производной.
Зависимость пути от времени при прямолинейном движении точки
задана уравнением 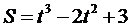 . Вычислить её скорость при t = 3 сек.
. Вычислить её скорость при t = 3 сек.
Зависимость пути от времени при прямолинейном движении точки
задана уравнением 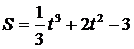 . Вычислить её ускорение при t = 3 сек. Составить уравнение касательной, проведенной к графику функции
. Вычислить её ускорение при t = 3 сек. Составить уравнение касательной, проведенной к графику функции
 в его точке с абсциссой
в его точке с абсциссой 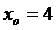 .
.
Зависимость пути от времени при прямолинейном движении точки
задана уравнением 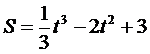 . Вычислить её ускорение при t = 5 сек.
. Вычислить её ускорение при t = 5 сек.
Составить уравнение касательной, проведенной к графику
функции 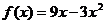 в его точке с абсциссой х = 0.
в его точке с абсциссой х = 0.
Составить уравнение касательной, проведенной к графику
функции 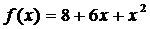 в его точке с абсциссой
в его точке с абсциссой 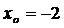 .
.
6. Зависимость пути от времени при прямолинейном движении точки задана уравнением 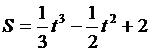 . Вычислить её скорость при t = 5 сек.
. Вычислить её скорость при t = 5 сек.
7. Составить уравнение касательной к параболе 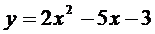 в
в
точке х = 2.
Составить уравнение касательной, проведенной к графику
функции 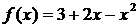 в его точке с абсциссой
в его точке с абсциссой 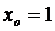 .
.
9. Составить уравнение касательной, проведенной к графику функции 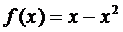 в его точке с абсциссой
в его точке с абсциссой  .
.
Тема 8. Геометрические тела и поверхности.
1. В прямом параллелепипеде стороны оснований равны 7 см и 4 см, угол между ними 60 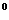 . Определить объём параллелепипеда, если боковая поверхность равна 220 см
. Определить объём параллелепипеда, если боковая поверхность равна 220 см 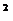 .
.
2. Боковое ребро правильной четырехугольной пирамиды наклонено к плоскости основания под углом 45 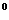 . Диагональ основания пирамиды равна 8 см. Найти высоту пирамиды.
. Диагональ основания пирамиды равна 8 см. Найти высоту пирамиды.
В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь диагонального сечения.
4. Рёбра прямоугольного параллелепипеда относятся как 3:7:8, площадь поверхности равна 808 м 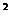 .Определить длины ребер параллелепипеда.
.Определить длины ребер параллелепипеда.
5. Основания усеченной пирамиды равны 27см2 и 12 см2, высота равна 5 см. Вычислить высоту соответствующей полной пирамиды.
6. Стороны основания прямого параллелепипеда равны 6 см и 8 см и образуют угол в 30о. Боковое ребро равно 5 см. Найдите полную поверхность этого параллелепипеда.
7. В пирамиде сечение, параллельное основанию, делит высоту в отношении 3:4 (от вершины к основанию); площадь сечения меньше площади основания на 200 см2. Определить площадь основания.
8. Образующая конуса равна 10 дм, а угол при вершине осевого сечения 1200. Найти площадь осевого сечения конуса.
В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь полной поверхности параллелепипеда.
Высота пирамиды разделена на три равные части и через точки
Деления проведены плоскости, параллельные основанию. Площадь
основания равна 270 см 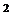 . Определить площади полученных сечений.
. Определить площади полученных сечений.
