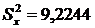Рассчитаем параметры парной линейной регрессии.
Пример решения задачи №1
Линейная парная регрессия
По данным представленным в таблице, изучается зависимость результативного признака (У) от факторного (Х).
| № п/п | Расходы на рекламу, тыс. грн | Доход от продажи продукции, тыс. грн |
| Номер предприятия | Х | У |
| 14,4 | ||
| 16,0 | ||
| 17,2 | ||
| 20,0 | ||
| 14,8 | ||
| 16,2 | ||
| 17,4 | ||
| 15,0 | ||
| 24,0 | ||
| 21,6 |
Задание
1. Постройте поле корреляции
2. Рассчитайте параметры парной линейной регрессии, и объяснить их смысл.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Вычислить стандартную ошибку оценки регрессии.
5.Вычислить точечную оценку прогноза для аналогичных предприятий, которые вкладывают в рекламу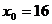 
тыс. грн.
6. Построить 95% доверительный интервал:
1) для коэффициента корреляции;
2) для функции регрессии;
3) для индивидуальных значений Y таких же предприятий;
4) для параметров регрессионной модели;
5) для параметра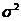 
.
7. Оценить на уровне значимости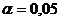 
значимость уравнения регрессии У по Х:
1) Используя F – критерий Фишера;
2) Используя t – распределение Стьюдента.
8. Определить значимость коэффициента корреляции.
9. Найти коэффициент детерминации и объяснить его смысл.
Решение:
Корреляционное поле.
Изобразим полученную зависимость графически точками координатной плоскости (рис. 1.1). Такое изображение статистической зависимости называется полем корреляции.
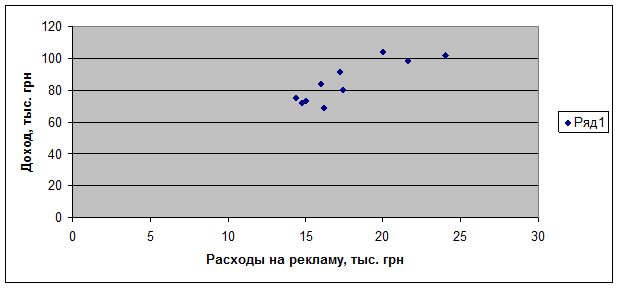
Рис. 1.1 Корреляционное поле
По расположению эмпирических точек можно предполагать наличие линейной корреляции.
Уравнение регрессии будем искать в виде:
.
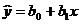Рассчитаем параметры парной линейной регрессии.
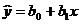
Определим параметры уравнения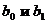 
по методу наименьших квадратов (МНК).
Система нормальных уравнений метода наименьших квадратов может быть записана в следующем виде:
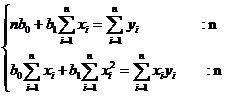Разделив каждое уравнение на n, получим 
.
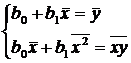Из первого уравнения выразим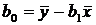 
, подставив в уравнение 
,
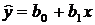Получим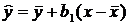 
, где 
.
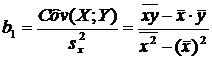Здесь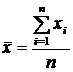 
; 
; 
; 
; 
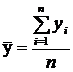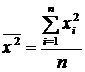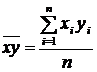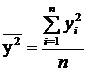
1. Составим расчетную таблицу 1.1:
Расчетная таблица
Таблица 1.1
| № п/п |  |  |  |  |  |  |  |  |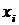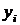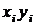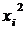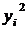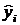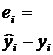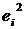
| 14,4 | 207,36 | 73,183 | -1,817 | 3,302 | ||||
| 78,885 | -5,115 | 26,167 | ||||||
| 17,2 | 1565,2 | 295,84 | 83,161 | -7,839 | 61,451 | |||
| 93,139 | -10,861 | 117,961 | ||||||
| 14,8 | 1065,6 | 219,04 | 74,608 | 2,608 | 6,803 | |||
| 16,2 | 1117,8 | 262,44 | 79,597 | 10,597 | 112,303 | |||
| 17,4 | 302,76 | 83,874 | 3,874 | 15,005 | ||||
| 75,321 | 2,321 | 5,387 | ||||||
| 107,393 | 5,393 | 29,089 | ||||||
| 21,6 | 2116,8 | 466,56 | 98,841 | 0,841 | 0,707 | |||
| Сумма | 176,6 | 15304,4 | 73,183 | |||||
| Средние | 17,66 | 84,8 | 1530,44 | 321,1 | 78,885 | |||
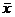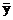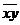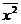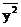 |  |  |  |  | сумма | 378,176 |
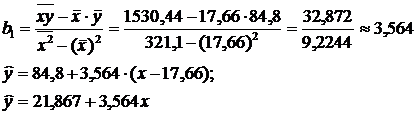
(Отметим, что свободный член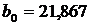 
реального экономического смысла не имеет)
Так как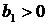 
, то зависимость между X и Y прямая: с ростом вложений в рекламу наблюдается рост дохода. Коэффициент 
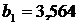показывает, что при увеличении расхода на рекламу (Х) на 1 тыс. грн доход от продажи продукции в среднем увеличивается на 3,564 тыс. грн для подобных предприятий.
Полученную прямую построим по двум произвольным точкам:
| x | ||
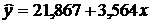 | ≈57, 5 | ≈111, 0 |
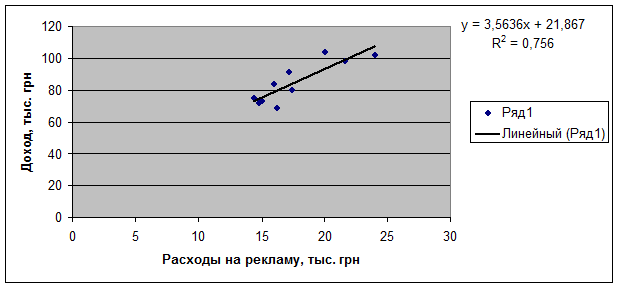
Рис. 1.2. Построение полученной прямой
Для дальнейших вычислений нам пригодятся уже вычисленные величины:
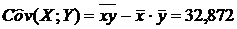и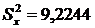 
Стандартная ошибка оценки регрессии.
Найдём оценку дисперсии отклонений по формуле:
; 
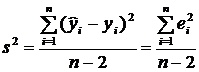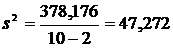
Стандартная ошибка оценки регрессии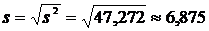 
.
5. Вычислим точечную оценку прогноза при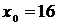 
:
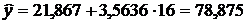
Раздел дисперсионный анализ.
В 1 колонке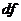 
записано число степеней свободы соответственно для компонент дисперсиирегрессии 1
Остаточной 8
Общей 9
Во 2 колонке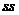 
приведенысуммы квадратов:
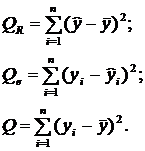
В 3 колонке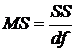 
приведены средние суммы квадратов отклонений с учётом числа степеней свободы:
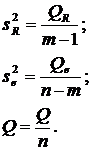
В 4 колонкеприводитсязначение F – критерия Фишера с уровнем доверия 0,95.
В 5 колонке приведена «Значимость F»,которая показывает, что при значении этого показателя менее 0,05 построенная регрессионная модель отвечает реальной регрессии.
Последняя таблица отчёта содержит:
В 1 колонке «Коэффициенты» приведены значения параметров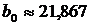 
и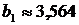 
.
Во 2 колонке «Стандартная погрешность»приведены среднеквадратические отклонения параметров модели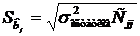 
, где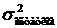 
- дисперсия остатков; Сjj-диагональный элемент матрицы погрешностей C (матрица, обратная к матрице системы нормальных уравнений).
В 3 колонке «t-статистика»приводятся стандартизованные (нормированные) параметры уравнения регрессии, которые находятся делением каждого фактически найденного параметра (1 колонка) на его стандартную погрешность (2 колонка).
В 4 колонке «Р – значения»находятся функции, которые рассчитываются по таким показателям:стандартизованные t – критерии Стьюдента, вычисленные путём деления t – критерии на значения их стандартных погрешностей; количество степеней свободы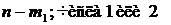 
:
если связь между Х и Y положительная или отрицательная, то используют число 1;
если не известно какой связи между Х и Yследует ожидать, то используют число 2.
В общем, если Р<0,05 то оценки параметров уравнения регрессии являются достоверными и модель отвечает реальной действительности.
В 5 колонке «Нижние 95%, Верхние 95%»помещены нижние и верхние границы 95-процентного уровня доверия для каждого параметра регрессии. Если доверительные интервалы не содержат в себе нуль, то с 95- процентной уверенностью можно утверждать, что независимая переменная добавляет в уравнение регрессии значимую информацию и можно достаточно точно описывать рассмотренный процесс или явление.
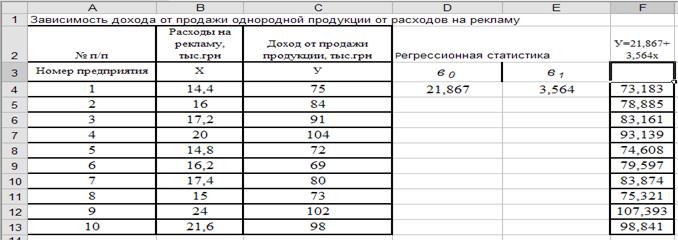
Рис. 1.7. Отчёт
Задача для самостоятельного решения №1
Получены данные о продаже товара Y млн. грн при общем объеме товарооборота X млрд. грн Построить линейную парную регрессию Yна X.
Необходимо:
1. Построить поле корреляции.
2. Рассчитать параметры парной линейной регрессии и объяснить их смысл.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Вычислить стандартную ошибку оценки регрессии.
5. Вычислить точечный прогноз реализации товара для х=х0 .
6.Найти 95% интервалы:
1) для коэффициента корреляции;
2) математического ожидания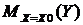 
;
3) индивидуального значения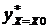 
;
4) для параметра β1 регрессионной модели;
5) для параметра .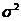
7.Оценить на уровне значимости 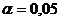значимость уравнения регрессии У по Х:
1) Используя F – критерий Фишера;
2) Используя t – распределение Стьюдента.
Уровень значимости принять равным α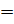 
0,05. Данные приведены в таблице 1.4.
Таблица 1.4
Варианты заданий для группы 21
| № | Данные о продаже | ||||||||||
| Х0=3,8 | Х | 2,6 | 2,8 | 2,9 | 3,0 | 3,3 | 3,6 | 3,7 | 3,9 | 3,9 | 4,0 |
| Y | 10,4 | 10,7 | 11,5 | 11,8 | 12,2 | 15,5 | 17,6 | 17,7 | 18,3 | 18,3 | |
| Х0=3,4 | Х | 3,2 | 3,3 | 3,5 | 3,7 | 3,8 | 4,0 | 4,3 | 4,5 | 4,5 | 4,7 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,8 | 8,7 | 8,9 | 9,1 | 9,4 | |
| Х0=4,1 | Х | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,6 | 4,7 | 4,9 | 5,1 | 5,2 |
| Y | 15,5 | 17,5 | 19,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 31,2 | |
| Х0=8 | Х | 3,0 | 3,1 | 3,2 | 3,3 | 3,6 | 3,8 | 4,0 | 4,2 | 4,3 | 4,4 |
| Y | 7,6 | 8,5 | 9,3 | 10,2 | 10,3 | 10,4 | 10,5 | 10,7 | 11,2 | 11,4 | |
| Х0=9,1 | Х | 2,4 | 2,7 | 2,9 | 3,0 | 3,6 | 4,0 | 4,4 | 4,8 | 5,0 | 5,3 |
| Y | 9,0 | 9,2 | 10,1 | 10,2 | 10,3 | 10,4 | 10,5 | 10,7 | 11,2 | 11,4 | |
| Х0=3,2 | Х | 2,5 | 2,8 | 3,0 | 3,5 | 3,7 | 4,3 | 4,6 | 5,0 | 5,2 | 5,3 |
| Y | 11,4 | 11,7 | 12,5 | 12,8 | 13,2 | 16,5 | 18,6 | 18,7 | 19,3 | 19,3 |
| Х0=4,2 | Х | 2,5 | 2,7 | 3,1 | 3,6 | 4,0 | 4,4 | 4,7 | 5,0 | 5,1 | 5,1 |
| Y | 4,3 | 4,4 | 5,0 | 5,9 | 6,1 | 6,2 | 7,2 | 7,4 | 7,6 | 7,9 | |
| Х0=3 | Х | 2,9 | 3,1 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,5 | 3,5 | 3,6 |
| Y | 16,2 | 18,3 | 18,2 | 19,0 | 19,6 | 20,3 | 21,5 | 22,5 | 23,3 | 24,1 | |
| Х0=4 | Х | 3,9 | 4,3 | 4,5 | 4,6 | 5,2 | 5,8 | 6,0 | 6,4 | 6,6 | 6,6 |
| Y | 10,6 | 11,5 | 12,3 | 13,2 | 13,4 | 14,2 | 16,0 | 17,1 | 17,8 | 18,9 | |
| Х0=4 | Х | 3,6 | 3,7 | 3,8 | 3,9 | 4,1 | 4,5 | 4,6 | 4,8 | 4,9 | 5,0 |
| Y | 12,9 | 13,2 | 14,0 | 14,3 | 14,7 | 18,0 | 18,1 | 20,2 | 20,8 | 20,8 | |
| Х0=4,1 | Х | 3,2 | 3,2 | 3,4 | 4,0 | 3,8 | 4,0 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 11,6 | 11,9 | 12,9 | 14,7 | 15,2 | 15,5 | 17,5 | 17,8 | 18,1 | 18,8 | |
| Х0=3 | Х | 2,7 | 2,8 | 2,9 | 3,2 | 3,3 | 2,6 | 3,7 | 3,9 | 3,9 | 4,1 |
| Y | 9,2 | 10,2 | 11,2 | 12,0 | 12,6 | 13,3 | 14,5 | 15,6 | 16,3 | 17,1 | |
| Х0=4 | Х | 3,6 | 3,7 | 3,8 | 3,9 | 4,2 | 4,5 | 4,6 | 4,8 | 4,8 | 5,0 |
| Y | 10,4 | 11,3 | 12,1 | 13,0 | 13,2 | 14,0 | 15,8 | 16,9 | 17,6 | 18,7 | |
| Х0=3 | Х | 2,0 | 2,4 | 2,6 | 2,7 | 3,3 | 3,9 | 4,1 | 4,5 | 4,7 | 4,7 |
| Y | 8,0 | 8,4 | 10,1 | 10,4 | 10,6 | 10,8 | 11,0 | 11,4 | 12,4 | 12,9 | |
| Х0=4,2 | Х | 3,4 | 3,8 | 4,0 | 4,1 | 4,7 | 5,3 | 5,5 | 5,9 | 6,1 | 6,1 |
| Y | 8,6 | 9,4 | 10,2 | 11,1 | 11,3 | 12,1 | 13,9 | 15,0 | 15,7 | 16,8 | |
| Х0=4 | Х | 3,3 | 3,4 | 3,5 | 3,6 | 3,9 | 4,2 | 4,3 | 4,5 | 4,5 | 4,7 |
| Y | 12,6 | 12,9 | 13,7 | 14,0 | 14,4 | 17,7 | 17,8 | 19,9 | 20,5 | 20,5 | |
| Х0=3 | Х | 2,3 | 2,5 | 2,9 | 3,4 | 3,6 | 4,2 | 4,4 | 4,8 | 5,0 | 5,0 |
| Y | 10,1 | 10,2 | 11,2 | 13,0 | 13,4 | 13,8 | 5,8 | 16,1 | 16,4 | 19,0 | |
| Х0=6 | Х | 5,6 | 5,9 | 6,2 | 6,5 | 6,7 | 7,2 | 7,3 | 7,6 | 7,8 | 8,3 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=4 | Х | 3,1 | 3,2 | 3,4 | 3,7 | 3,8 | 3,9 | 4,2 | 4,4 | 4,6 | 4,8 |
| Y | 19,8 | 20,4 | 21,9 | 22,3 | 23,4 | 30,0 | 34,1 | 34,3 | 35,3 | 35,5 | |
| Х0=8 | Х | 7,6 | 7,9 | 8,2 | 8,5 | 8,7 | 9,2 | 9,3 | 9,6 | 9,8 | 10,3 |
| Y | 2,4 | 2,5 | 2,5 | 2,6 | 2,9 | 3,5 | 4,3 | 4,4 | 4,8 | 5,1 | |
| Х0=5 | Х | 4,6 | 4,9 | 5,2 | 5,5 | 5,7 | 6,2 | 6,3 | 6,6 | 6,8 | 7,3 |
| Y | 4,1 | 4,0 | 3,7 | 3,6 | 3,4 | 3,3 | 3,2 | 3,0 | 3,0 | 2,7 |
| Х0=5 | Х | 4,1 | 4,2 | 4,4 | 4,7 | 4,8 | 4,9 | 5,2 | 5,4 | 5,6 | 5,8 |
| Y | 15,5 | 17,5 | 19,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 30,2 | |
| Х0=3 | Х | 2,6 | 2,9 | 3,2 | 3,5 | 3,7 | 4,2 | 4,3 | 4,6 | 4,8 | 5,3 |
| Y | 38,7 | 40,1 | 43,2 | 46,0 | 50,0 | 56,0 | 59,0 | 60,0 | 61,0 | 66,0 | |
| Х0=6 | Х | 5,1 | 5,2 | 5,4 | 5,7 | 5,8 | 5,9 | 6,2 | 6,4 | 6,6 | 6,8 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4 | Х | 3,6 | 3,9 | 4,2 | 4,5 | 4,7 | 5,2 | 5,3 | 5,6 | 5,8 | 6,3 |
| Y | 13,8 | 14,6 | 14,9 | 16,3 | 18,6 | 24,6 | 33,2 | 34,4 | 38,8 | 40,8 | |
| Х0=5 | Х | 4,9 | 5,2 | 5,5 | 5,8 | 6,0 | 6,5 | 6,6 | 6,9 | 7,1 | 7,6 |
| Y | 7,8 | 7,9 | 8,2 | 8,5 | 8,9 | 9,0 | 9,5 | 9,8 | 9,9 | 10,5 | |
| Х0=4,8 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 19,8 | 20,4 | 21,9 | 22,3 | 23,4 | 30,0 | 34,1 | 34,3 | 35,3 | 35,5 | |
| Х0=6 | Х | 5,9 | 6,2 | 6,5 | 6,8 | 7,0 | 7,5 | 7,6 | 7,9 | 8,1 | 8,6 |
| Y | 2,4 | 2,5 | 2,5 | 2,6 | 2,9 | 3,5 | 4,3 | 4,4 | 4,8 | 5,1 | |
| Х0=5 | Х | 4,4 | 4,6 | 4,8 | 5,1 | 5,3 | 5,4 | 5,6 | 5,8 | 6,0 | 6,1 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,1 | 9,3 | |
| Х0=7 | Х | 6,9 | 7,2 | 7,5 | 7,8 | 8,0 | 8,5 | 8,6 | 8,9 | 9,1 | 9,6 |
| Y | 2,1 | 2,0 | 1,7 | 1,6 | 1,4 | 1,3 | 1,2 | 1,0 | 1,0 | 0,7 | |
| Х0=5 | Х | 4,5 | 4,6 | 4,8 | 5,1 | 5,3 | 5,4 | 5,5 | 5,7 | 6,0 | 6,2 |
| Y | 15,5 | 17,5 | 17,5 | 21,0 | 22,1 | 23,6 | 26,0 | 28,1 | 29,5 | 30,2 | |
| Х0=4,5 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4 | Х | 3,9 | 4,2 | 4,5 | 4,8 | 5,0 | 5,5 | 5,6 | 5,9 | 6,1 | 6,6 |
| Y | 15,8 | 16,6 | 16,9 | 18,3 | 20,6 | 26,6 | 35,2 | 36,4 | 40,8 | 42,8 | |
| Х0=6 | Х | 5,1 | 5,5 | 5,8 | 6,1 | 6,5 | 6,7 | 7,3 | 7,6 | 8,0 | 8,3 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=3,5 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 14,8 | 15,4 | 16,9 | 17,3 | 18,4 | 25,0 | 29,1 | 29,3 | 30,3 | 30,5 |
Таблица 1.5
Варианты заданий для группы 22
| № | Данные о продаже | ||||||||||
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 3,4 | 3,5 | 3,5 | 3,6 | 3,9 | 4,5 | 5,3 | 5,4 | 5,8 | 6,1 | |
| Х0=4,5 | Х | 4,3 | 4,6 | 4,7 | 4,9 | 5,0 | 5,1 | 5,2 | 5,4 | 5,5 | 5,6 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,0 | 9,3 | |
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 5,1 | 5,0 | 4,7 | 4,6 | 4,4 | 4,3 | 4,2 | 4,0 | 4,0 | 3,7 | |
| Х0=3,8 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 13,5 | 15,5 | 17,5 | 19,0 | 20,1 | 21,6 | 24,0 | 26,1 | 27,5 | 28,2 | |
| Х0=4 | Х | 3,1 | 3,5 | 3,8 | 4,1 | 4,5 | 4,7 | 5,3 | 5,6 | 6,0 | 6,3 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=3,5 | Х | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,1 | 4,2 | 4,4 | 4,5 | 4,6 |
| Y | 8,6 | 9,5 | 10,3 | 11,2 | 11,4 | 12,2 | 14,0 | 15,1 | 15,8 | 16,9 | |
| Х0=4,2 | Х | 2,1 | 2,5 | 2,8 | 3,1 | 3,5 | 3,7 | 4,3 | 4,6 | 5,0 | 5,3 |
| Y | 13,8 | 14,6 | 14,9 | 16,3 | 18,6 | 20,8 | 23,2 | 24,4 | 24,6 | 28,8 | |
| Х0=5 | Х | 3,8 | 4,2 | 4,5 | 4,8 | 5,2 | 5,4 | 6,0 | 6,3 | 6,7 | 7,0 |
| Y | 8,8 | 8,9 | 9,2 | 9,5 | 9,9 | 10,0 | 10,5 | 10,8 | 10,9 | 11,5 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 13,8 | 14,4 | 15,9 | 16,3 | 17,4 | 24,0 | 28,1 | 28,3 | 29,5 | 39,3 | |
| Х0=6 | Х | 5,8 | 6,2 | 6,5 | 6,8 | 7,2 | 7,4 | 8,0 | 8,3 | 8,7 | 9,0 |
| Y | 4,4 | 4,5 | 4,5 | 4,6 | 4,9 | 5,5 | 6,3 | 6,4 | 6,8 | 7,1 | |
| Х0=4,1 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 5,8 | 5,9 | 6,5 | 7,4 | 7,6 | 7,7 | 8,8 | 8,9 | 9,1 | 9,3 | |
| Х0=6 | Х | 5,8 | 6,2 | 6,5 | 6,8 | 7,2 | 7,4 | 8,0 | 8,3 | 8,7 | 9,0 |
| Y | 6,1 | 6,0 | 5,7 | 5,6 | 5,4 | 5,3 | 5,2 | 5,0 | 5,0 | 4,7 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 13,5 | 15,5 | 17,5 | 19,0 | 20,1 | 21,6 | 24,0 | 26,1 | 27,5 | 28,2 | |
| Х0=3 | Х | 2,8 | 3,2 | 3,5 | 3,8 | 4,2 | 4,4 | 5,0 | 5,3 | 5,7 | 6,0 |
| Y | 18,7 | 20,1 | 23,2 | 26,0 | 30,0 | 36,0 | 39,0 | 40,0 | 41,0 | 46,0 | |
| Х0=4,1 | Х | 3,5 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 4,3 | 4,5 | 4,6 | 4,8 |
| Y | 7,6 | 8,5 | 9,3 | 10,2 | 10,4 | 11,2 | 13,0 | 14,1 | 14,8 | 15,9 |
| Х0=90 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 7,8 | 8,7 | 8,9 | 9,6 | 10,6 | 10,6 | 10,8 | 11,2 | ||
| Y | 13,3 | 13,5 | 13,8 | 14,4 | 14,7 | 14,9 | 15,3 | 15,5 | 16,4 | 16,8 | |
| Х0=100 | Х | ||||||||||
| Y | |||||||||||
| Х0=10 | Х | 8,1 | 8,3 | 9,2 | 9,9 | 10,9 | 11,1 | 12,3 | 11,5 | ||
| Y | 13,2 | 13,5 | 14,1 | 14,3 | 14,6 | 15,2 | 16,1 | 16,5 | |||
| Х0=80 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 7,6 | 7,8 | 8,5 | 8,7 | 9,4 | 10,4 | 10,6 | 10,9 | 11,1 | |
| Y | 13,1 | 13,3 | 13,6 | 14,2 | 14,5 | 14,7 | 15,1 | 15,3 | 16,2 | 16,6 | |
| Х0=80 | Х | ||||||||||
| Y | |||||||||||
| Х0=10 | Х | 7,3 | 7,5 | 8,2 | 8,4 | 9,1 | 10,1 | 10,3 | 10,6 | 10,7 | 10,8 |
| Y | 12,8 | 13,3 | 13,9 | 14,2 | 14,4 | 14,8 | 15,9 | 16,3 | |||
| Х0=70 | Х | ||||||||||
| Y | |||||||||||
| Х0=9 | Х | 6,9 | 7,1 | 7,8 | 8,7 | 9,7 | 9,9 | 10,2 | 10,3 | 10,4 | |
| Y | 12,4 | 12,6 | 12,9 | 13,5 | 13,8 | 14,4 | 14,6 | 15,5 | 15,9 | ||
| Х0=75 | Х | ||||||||||
| Y | |||||||||||
| Х0=8 | Х | 6,6 | 6,8 | 7,5 | 7,7 | 8,4 | 9,4 | 9,7 | 9,9 | 10,1 | |
| Y | 12,1 | 12,3 | 12,6 | 13,2 | 13,5 | 13,7 | 14,1 | 14,3 | 15,2 | 15,7 | |
| Х0=76 | Х | ||||||||||
| Y | |||||||||||
| Х0=7 | Х | 6,7 | 6,5 | 7,2 | 7,4 | 8,1 | 8,9 | 9,3 | 9,7 | 10,1 | 10,5 |
| Y | 11,7 | 12,1 | 12,4 | 12,8 | 13,3 | 13,5 | 13,8 | 14,1 | 14,7 | 15,2 | |
| Х0=72 | Х | ||||||||||
| Y |
| Х0=6 | Х | 5,9 | 6,1 | 6,8 | 7,0 | 7,7 | 8,5 | 8,7 | 9,3 | 9,9 | 10,2 |
| Y | 11,3 | 11,7 | 12,1 | 12,4 | 12,9 | 13,1 | 13,4 | 13,7 | 14,4 | 14,8 | |
| Х0=7 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 9,3 |
| Y | 4,4 | 4,5 | 4,5 | 4,6 | 4,9 | 5,5 | 6,3 | 6,4 | 6,8 | 4,4 | |
| Х0=8 | Х | 6,1 | 6,5 | 6,8 | 7,1 | 7,5 | 7,7 | 8,3 | 8,6 | 9,0 | 6,1 |
| Y | 6,1 | 6,0 | 5,7 | 5,6 | 5,4 | 5,3 | 5,2 | 5,0 | 5,0 | 6,1 | |
| Х0=4 | Х | 3,5 | 3,6 | 3,8 | 4,0 | 4,3 | 4,4 | 4,6 | 4,7 | 5,0 | 5,2 |
| Y | 8,9 | 9,0 | 9,3 | 9,6 | 10,0 | 10,1 | 10,6 | 10,9 | 11,0 | 11,6 | |
| Х0=6 | Х | 5,1 | 5,5 | 5,8 | 6,1 | 6,5 | 6,7 | 7,3 | 7,6 | 8,0 | 8,3 |
| Y | 14,8 | 15,4 | 16,9 | 17,3 | 18,4 | 25,0 | 29,1 | 29,3 | 30,3 | 30,5 |
Пример решения задачи №1
Линейная парная регрессия
По данным представленным в таблице, изучается зависимость результативного признака (У) от факторного (Х).
| № п/п | Расходы на рекламу, тыс. грн | Доход от продажи продукции, тыс. грн |
| Номер предприятия | Х | У |
| 14,4 | ||
| 16,0 | ||
| 17,2 | ||
| 20,0 | ||
| 14,8 | ||
| 16,2 | ||
| 17,4 | ||
| 15,0 | ||
| 24,0 | ||
| 21,6 |
Задание
1. Постройте поле корреляции
2. Рассчитайте параметры парной линейной регрессии, и объяснить их смысл.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Вычислить стандартную ошибку оценки регрессии.
5.Вычислить точечную оценку прогноза для аналогичных предприятий, которые вкладывают в рекламу 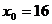тыс. грн.
6. Построить 95% доверительный интервал:
1) для коэффициента корреляции;
2) для функции регрессии;
3) для индивидуальных значений Y таких же предприятий;
4) для параметров регрессионной модели;
5) для параметра .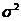
7. Оценить на уровне значимости 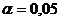значимость уравнения регрессии У по Х:
1) Используя F – критерий Фишера;
2) Используя t – распределение Стьюдента.
8. Определить значимость коэффициента корреляции.
9. Найти коэффициент детерминации и объяснить его смысл.
Решение:
Корреляционное поле.
Изобразим полученную зависимость графически точками координатной плоскости (рис. 1.1). Такое изображение статистической зависимости называется полем корреляции.
Рис. 1.1 Корреляционное поле
По расположению эмпирических точек можно предполагать наличие линейной корреляции.
Уравнение регрессии будем искать в виде:
.
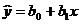Рассчитаем параметры парной линейной регрессии.
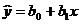
Определим параметры уравнения 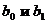по методу наименьших квадратов (МНК).
Система нормальных уравнений метода наименьших квадратов может быть записана в следующем виде:
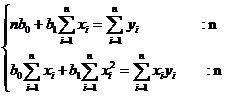Разделив каждое уравнение на n, получим .
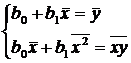Из первого уравнения выразим 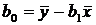, подставив в уравнение ,
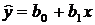Получим 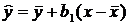, где .
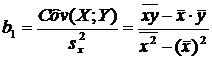Здесь ; ; ; ;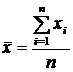
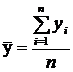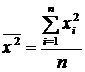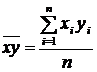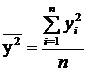
1. Составим расчетную таблицу 1.1:
Расчетная таблица
Таблица 1.1
| № п/п | | | | | | | | |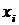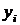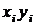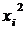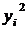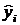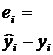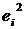
| 14,4 | 207,36 | 73,183 | -1,817 | 3,302 | ||||
| 78,885 | -5,115 | 26,167 | ||||||
| 17,2 | 1565,2 | 295,84 | 83,161 | -7,839 | 61,451 | |||
| 93,139 | -10,861 | 117,961 | ||||||
| 14,8 | 1065,6 | 219,04 | 74,608 | 2,608 | 6,803 | |||
| 16,2 | 1117,8 | 262,44 | 79,597 | 10,597 | 112,303 | |||
| 17,4 | 302,76 | 83,874 | 3,874 | 15,005 | ||||
| 75,321 | 2,321 | 5,387 | ||||||
| 107,393 | 5,393 | 29,089 | ||||||
| 21,6 | 2116,8 | 466,56 | 98,841 | 0,841 | 0,707 | |||
| Сумма | 176,6 | 15304,4 | 73,183 | |||||
| Средние | 17,66 | 84,8 | 1530,44 | 321,1 | 78,885 | |||
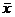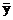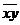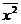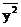| | | | | | сумма | 378,176 |
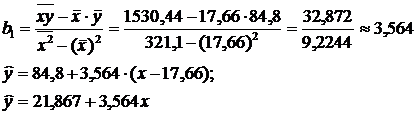
(Отметим, что свободный член 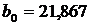реального экономического смысла не имеет)
Так как 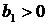, то зависимость между X и Y прямая: с ростом вложений в рекламу наблюдается рост дохода. Коэффициент 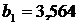показывает, что при увеличении расхода на рекламу (Х) на 1 тыс. грн доход от продажи продукции в среднем увеличивается на 3,564 тыс. грн для подобных предприятий.
Полученную прямую построим по двум произвольным точкам:
| x | ||
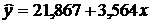| | ≈57, 5 | ≈111, 0 |
Рис. 1.2. Построение полученной прямой
Для дальнейших вычислений нам пригодятся уже вычисленные величины:
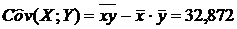и