Характеристическая функция, потенциал и функция тока
Представим себе, что имеем плоский фильтрационный поток любой жидкости или газа, подчиняющийся закону Дарси. При рассмотрении одномерных течений было показано, что если фильтрация протекает по закону Дарси, существует потенциальная функция j, удовлетворяющая уравнению Лапласа. Но если существует потенциальная функция j, то наряду с ней существует функция y, также удовлетворяющая уравнению Лапласа. Зная функцию j, всегда можно определить функцию y путем интегрирования уравнения (7.37).
Потенциальная функция течения определяется зависимостью основных параметров жидкости (или газа) и пористой среды от давления. Допустим, что эта зависимость однозначная; тогда можно заключить, что в основной плоскости течения линии равного давления (изобары) совпадают с эквипотенциальными линиями j(х, у) = С. Но кривые y(х, у)=С* взаимно ортогональны с эквипотенциальными линиями. Следовательно, направление векторов скорости фильтрации будет совпадать в любой данной точке М с направлением касательной к кривой семейства y(х, у)=С*, то есть кривые этого семейства можно считать линиями тока. (При установившемся движении линии тока и траектории частиц жидкости совпадают). Функция y(х, у) называется функцией тока.
Потенциальную функцию течения jи функцию тока y всегда можно принять за действительную и мнимую части некоторой функции F(z) комплексного переменного z (7.34).
Функция F (z) называется характеристической функцией течения (комплексным потенциалом).
Исследование любого плоского течения жидкости или газа в пористой среде должно начинаться с определения характеристической функции, соответствующей данной задаче. Найдя ее, мы можем считать задачу решенной. В самом деле, отделив в характеристической функции действительную часть от мнимой, т. е. представив ее в виде, показанном формулой (7.34), можно определить потенциальную функцию j(х, у)и функцию тока y(х, у).В результате можно представить полную картину потока: принимая различные значения функции j, получим уравнения семейства эквипотенциальных линий j(х, у) = С, а придавая различные значения y, найдем уравнения семейства линий тока y(х, у) = С*. По эквипотенциальным линиям определяется распределение давлений в пласте, по линиям тока – направление движения и характер поля скоростей фильтрации.
Проекции вектора массовой скорости фильтрации на оси координат можно записать в виде:
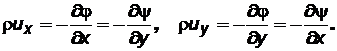 (7.38)
(7.38)
Примечание. Функции тока может быть дан следующий смысл. Фиксируем некоторую линию тока y(х, у) = 0 и вообразим канал, ограниченный цилиндрическими поверхностями с образующими, перпендикулярными плоскости течения, проведенными через линию тока y = 0 и другую линию тока y(х, у) = С* и двумя плоскостями – плоскостью движения и ей параллельной, отстоящей от первой плоскости на расстояние, равное единице (рис. 7.20).
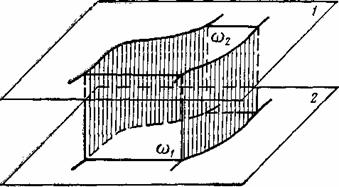
Рис. 7.20. Распределение потока между двумя параллельными плоскостями 1 и 2
При рассмотрении двух произвольных поперечных сечения канала ω1 и ω2 видно, что количество массы жидкости, протекающей через эти сечения в единицу времени (расход) будет одно и то же; внутри такого канала количество массы жидкости при установившемся движении измениться не может; через боковые стенки канала, образованные линиями тока y = 0 и y(х, у) = С*1, и через плоскости движения жидкость не протекает, следовательно, втекает жидкости в единицу времени через ω1 столько, сколько вытекает через ω2.
Функцией тока можно назвать функцию, принимающую на линии тока y(х, у) = С*значение, равное массе жидкости (газа), протекающей в единицу времени через поперечное сечение канала, построенного на линиях y = 0 и y(х, у) = С*1 . Функция тока определена с точностью до произвольной постоянной, зависящей от выбора начальной линии тока y= 0.
Массовую скорость фильтрации можно очень просто определить в любой точке пласта, найдя производную от характеристической функции по комплексному аргументу z. Чтобы это показать, составим полный дифференциал от характеристической функции F (z):
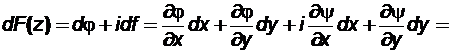 (7.39)
(7.39)
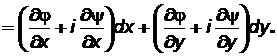
Вынося во второй скобке множитель i за знак скобки и воспользовавшись затем уравнениями Коши – Римана (7.37) получим:

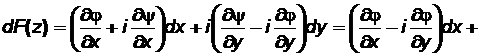
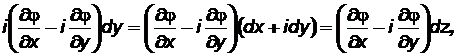
т.е.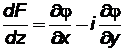 .(7.40)
.(7.40)
Учитывая (7.38), перепишем (7.40) в виде
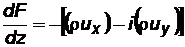 .(7.41)
.(7.41)
Из (7.40) и (7.41) следует, что производная dF/dz есть комплексное число, модуль которого равен модулю массовой скорости фильтрации:
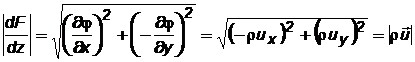 .(7.42)
.(7.42)
Таким образом, модуль производной от характеристической функции течения равен модулю массовой скорости фильтрации.
Для однородной несжимаемой жидкости функция тока будет иметь значение объемного (а не массового) расхода жидкости через поперечное сечение канала, построенного на линиях тока y=0 и y=С*.Модуль же производной от характеристической функции течения будет равен скорости (а не массовой скорости) фильтрации жидкости u.
