Статистическая проверка статистических гипотез
Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах неизвестных распределений. Критерием согласия называют статистический критерий проверки нулевой гипотезы о предполагаемом законе неизвестного распределения. Если нулевая гипотеза не верна, то будет верна конкурирующая (альтернативная) гипотеза Н1, противоречащая нулевой.
В основе критерия согласия Пирсона лежит сравнение эмпирических (наблюдаемых) и теоретических частот, вычисленных в предположении о вполне определенном виде закона распределения генеральной совокупности.
Методика вычисления теоретических частот нормального распределения для равноотстоящих вариант
Пусть эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот:
| Варианты | xi | x1 | x2 | … | xs |
| Эмп.част. |  |  |  | … |  |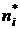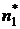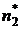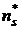
Требуется при уровне значимости a проверить гипотезу о нормальном распределении генеральной совокупности.
Алгоритм решения.
1. Вычислить выборочную среднюю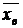 
и выборочное среднее квадратическое отклонение sв.
2. Вычислить теоретические частоты
,
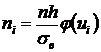где n – объем выборки, h – шаг (разность между двумя соседними вариантами),
, 
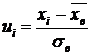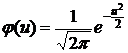
3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
– находят наблюдаемое значение критерия
;
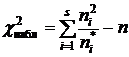– из таблицы критических точек распределения c2 по заданному уровню значимости a и числу степеней свободы k = s – 3 (s – число групп выборки) находят критическую точку c2кр (a, k).
Если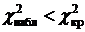 
, то нет оснований отвергать нулевую гипотезу, то есть генеральная совокупность распределена нормально.
Если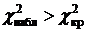 
, то нулевую гипотезу отвергают, то есть нет оснований утверждать, что генеральная совокупность распределена нормально.
Методика вычисления теоретических частот нормального распределения для интервального ряда
Пусть эмпирическое распределение задано в виде последовательности интервалов и соответствующих им частот:
| Интервалы | [xi, xi+1) | [x1, x2) | [x2, x3) | … | [xs, xs+1] |
| Сумма частот | | | | … | |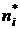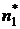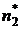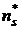
Требуется при уровне значимости a проверить гипотезу о нормальном распределении генеральной совокупности.
Алгоритм решения.
1. Вычислить выборочную среднюю 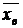и выборочное среднее квадратическое отклонение sв, причем в качестве вариант 
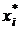принимают среднее арифметическое концов интервала:
.
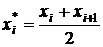2. Пронормировать выборку, то есть перейти к случайной величине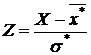 
и вычислить концы интервалов:
, 
,
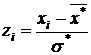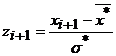причем наименьшее значение z1 полагают равным – ¥, а наибольшее значение zs+1 полагают равным +¥.
3. Вычислить теоретические частоты
,
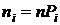где n – объем выборки, Рi – вероятность попадания Х в интервал (xi, xi+1):
,
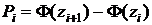где Ф(z) – табличная интегральная функция Лапласа.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, также как и для случая равноотстоящих вариант.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Варианты заданий контрольных работ
№ 1-10.
1. Из 12 деталей, изготовленных станком-автоматом, 4 бракованных. Найти вероятность того, что среди 3 наудачу взятых для контроля деталей будет хотя бы одна бракованная.
2. На прилавке магазина в случайном порядке расставлено 13 лазерных дисков, причем 5 из них – контрафактные. Контролер берет наудачу 3 диска. Найти вероятность того, что из взятых дисков не менее двух контрафактных.
3. Из 15 деталей, изготовленных станком-автоматом, 4 бракованных. Найти вероятность того, что среди 4 наудачу взятых для контроля деталей число бракованных будет не более одной.
4. Из 14 деталей, изготовленных станком-автоматом, 5 бракованных. Найти вероятность того, что среди 4 наудачу взятых для контроля деталей число стандартных будет не менее трех.
5. На прилавке магазина в случайном порядке расставлено 11 лазерных дисков, причем 4 из них – контрафактные. Контролер берет наудачу 3 диска. Найти вероятность того, что из взятых дисков не более одного контрафактного.
6. Из 16 деталей, изготовленных станком-автоматом, 6 бракованных. Найти вероятность того, что среди 3 наудачу взятых для контроля деталей число стандартных будет не менее двух.
7. Из 13 деталей, изготовленных станком-автоматом, 3 бракованных. Найти вероятность того, что среди 4 наудачу взятых для контроля деталей будет хотя бы одна бракованная.
8. Из 15 деталей, изготовленных станком-автоматом, 4 бракованных. Найти вероятность того, что среди 3 наудачу взятых для контроля деталей число стандартных будет не менее двух.
9. На прилавке магазина в случайном порядке расставлено 10 лазерных дисков, причем 4 из них – контрафактные. Контролер берет наудачу 3 диска. Найти вероятность того, что из взятых дисков не более одного контрафактного.
10. На прилавке магазина в случайном порядке расставлено 10 лазерных дисков, причем половина из них – контрафактные. Контролер берет наудачу 3 диска. Найти вероятность того, что среди взятых дисков не более одного лицензионного.
№ 11-20.
11. Имеются три ящика, содержащих детали. В первом ящике вероятность появления нестандартной детали равна 0,2, а во втором и третьем 0,3 и 0,1 соответственно. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что две из них окажутся стандартными.
12. Три рабочих изготавливают однотипные детали. Вероятность того, что при проверке ОТК будет забракована партия деталей, изготовленная первым рабочим, равна 0,9; вторым – 0,8; третьим – 0,85. Найти вероятность того, что будут забракованы две партии деталей.
13. Вероятность выхода из строя за гарантийный период микросхемы № 1 равна 0,1; микросхемы №2 – 0,2 и микросхемы №3 – 0,15. Найти вероятность того, что в электронном устройстве, содержащем все три микросхемы, за гарантийный период вышло из строя две микросхемы.
14. Вероятность того, что нужная сборщику деталь находится в первом, втором или третьем ящике соответственно равна 0,8; 0,7 и 0,9. Найти вероятность того, что требуемая деталь находится в двух ящиках.
15. Для каждого из трех производственных участков вероятность перевыполнения месячного плана соответственно равна 0,9; 0,85 и 0,8. Найти вероятность того, что месячные планы перевыполнят 2 участка.
16. Предприятие снабжается деталями от трех поставщиков. Вероятность несвоевременной поставки деталей каждым из поставщиков соответственно равны 0,15; 0,2 и 0,1. Найти вероятность того, что предприятие будет своевременно обеспеченно комплектующими изделиями только от двух поставщиков.
17. На оптовую базу поступает продукция с трех предприятий, причем в продукции первого предприятия содержится 15% второсортных изделий, в продукции второго и третьего соответственно 10% и 20%. Найти вероятность того, что среди трех изделий (по одному из продукции каждого предприятия) два будут первосортными.
18. Известно, что в продукции, изготавливаемой на трех штампах, брак соответственно составляет 5%, 7% и 3%. Найти вероятность того, что среди трех наудачу взятых изделий (по одному с каждого штампа) две будут стандартными.
19. Для каждого из трех производственных участков вероятность невыполнения месячного плана соответственно равна 0,2; 0,15 и 0,1. Найти вероятность того, что месячные планы выполнят два участка.
20. На дактилоскопическую экспертизу поступило 3 отпечатка пальцев. Вероятности непригодности к обработке каждого из отпечатков соответственно равны 0,1; 0,2 и 0,3. Найти вероятность того, что будет обработано не более 1 отпечатка.
№ 21-30.
21.Среди 100 деталей, изготовленных первым рабочим, 85 прошли закалку. Из 120 таких же деталей, изготовленных вторым рабочим, закалку прошли 95. Все детали поступили на сборку. Оказалось, что наудачу взятая сборщиком деталь прошла операцию закалки. Найти вероятность того, что она была изготовлена вторым рабочим.
22.В трех ящиках содержится 40, 35 и 50 деталей соответственно, причем в первом ящике 5, во втором 7 и в третьем 5 из них бракованные. Из наудачу выбранного ящика была взята деталь, которая оказалась стандартной. Найти вероятность того, что она была из второго ящика.
23.Три автомата изготавливают за смену 300, 400 и 300 одинаковых деталей соответственно, которые сбрасываются в один бункер. На первом автомате брак составляет 5%. на втором – 7%, на третьем – 3%. Наудачу взятая для контроля деталь оказалась стандартной. Найти вероятность того, что она изготовлена третьим автоматом.
24.Три штампа одинаковой производительности изготавливают однотипные детали, которые в одной таре передаются на дальнейшую обработку. Брак на первом штампе составляет 7%, на втором – 2%, на третьем – 4%.Наудачу взятая при входном контроле деталь оказалась бракованной. Найти вероятность того, что она была изготовлена на первом штампе.
25.На складе хранится 1200 изделий завода № 1, 800 – завода № 2 и 1000 – завода № 3. Среди изделий завода № 1 второсортные составляют 20%, для завода № 2 и № 3 этот параметр равен 15% и 30% соответственно. Наудачу взятое со склада изделие оказалось первосортным. Найти вероятность того, что его произвели на заводе № 2.
26.На оптовую базу поступает продукция с трех предприятий, причем в продукции 1-го предприятия содержится 10% второсортных изделий, 2-го и 3-го соответственно 25% и 20%. Приобретенное изделие оказалось первосортным. Найти вероятность того, что оно произведено 1-м предприятием, если известно, что 1-е предприятие поставило на базу продукции в два раза меньше, чем 2-е, а 3-е.
27.Два рабочих, изготавливающих одинаковые детали, произвели за смену по двадцать деталей, из которых в синий цвет окрасили 5 деталей первого и 7 деталей второго рабочего, а остальные окрасили в зеленый цвет. Все изготовленные детали в одном ящике поступили в сборочный цех. Извлеченная сборщиком деталь оказалась зеленного цвета. Найти вероятность того, что ее изготовил первый рабочий.
28.Вероятность выхода из строя за гарантийный период микросхемы № 1 равна 0,11; микросхемы № 2 – 0,1 и микросхемы № 3 – 0,09. В электронном устройстве, собранном из данных микросхем, в течение гарантийного периода отказала одна микросхема. Найти вероятность того, что это была микросхема № 3, если известно, что в электронном устройстве было использовано 5 микросхем № 1, 12 микросхем № 2 и 3 микросхемы № 3.
29.Три автомата одинаковой производительности изготавливают однотипные детали, которые сбрасываются в один бункер. Известно, что процент брака на первом автомате составляет 3%, на втором – 2%, на третьем – 4%. Взятая наудачу из бункера деталь оказалась стандартной. Найти вероятность того, что ее изготовил третий автомат.
30.В трех ящиках содержится 60, 65 и 55 деталей соответственно, причем в первом ящике 7, во втором 10 а в третьем 5 из них бракованные. Из наудачу выбранного ящика была взята деталь, которая оказалась стандартной. Найти вероятность того, что она была из третьего ящика.
№ 31-40.
31.Вероятность попадания по движущейся мишени равна 0,5. Найти вероятность того, что пять из семи выстрелов будут удачными.
32.Вероятность попадания по движущейся мишени равна 0,6. Найти вероятность того, что четыре из шести выстрелов будут удачными.
33.Вероятность попадания по движущейся мишени равна 0,7. Найти вероятность того, что пять из восьми выстрелов будут удачными.
34.Вероятность попадания по движущейся мишени равна 0,5. Найти вероятность того, что четыре из семи выстрелов будут удачными.
35.Вероятность попадания по мишени равна 0,8. Найти вероятность того, что семь из девяти выстрелов будут удачными.
36.Вероятность попадания по мишени равна 0,9. Найти вероятность того, что пять из шести выстрелов будут удачными.
37.Вероятность попадания по мишени равна 0,8. Найти вероятность того, что шесть из восьми выстрелов будут удачными.
38.Вероятность попадания по движущейся мишени равна 0,6. Найти вероятность того, что пять из девяти выстрелов будут удачными.
39.Вероятность попадания по движущейся мишени равна 0,4. Найти вероятность того, что четыре из восьми выстрелов будут удачными.
40.Вероятность попадания по мишени равна 0,9. Найти вероятность того, что семь из восьми выстрелов будут удачными.
№ 41-50.
41.Испытуемый в среднем не решает 20% предложенных ему задач. Найти вероятность того, что среди 100, случайным образом отобранных задач, не менее 80 окажутся решенными.
42.Среднее количество верно воспроизведенных испытуемым числовых и буквенных рядов составляет 75%. Испытуемому предложено 70 рядов. Какова вероятность того, что не менее 40 из них будут воспроизведены верно?
43.Испытуемый в среднем решает 90% предложенных ему задач. Найти вероятность того, что среди 100, случайным образом отобранных задач, не более 20 окажутся нерешенными.
44.Среднее количество верно воспроизведенных испытуемым числовых рядов составляет 75%. Испытуемому предложено 50 рядов. Какова вероятность того, что не менее 30 из них будут воспроизведены верно?
45.Испытуемый в среднем не решает 30% предложенных ему задач. Найти вероятность того, что среди 100, случайным образом отобранных задач, не менее 80 окажутся решенными.
46.Среднее количество верно воспроизведенных испытуемым буквенных рядов составляет 70%. Испытуемому предложено 50 рядов. Какова вероятность того, что не более 30 из них будут воспроизведены верно?
47.Испытуемый в среднем решает 75% предложенных ему задач. Найти вероятность того, что среди 100, случайным образом отобранных задач, не более 20 окажутся нерешенными.
48.Среднее количество верно воспроизведенных испытуемым буквенных рядов составляет 80%. Испытуемому предложено 50 рядов. Какова вероятность того, что не менее 30 из них будут повторены верно?
49.Испытуемый в среднем не решает 15% предложенных ему задач. Найти вероятность того, что среди 100, случайным образом отобранных задач, не менее 80 окажутся решенными.
50.Испытуемый в среднем решает 85% предложенных ему задач. Найти вероятность того, что среди 90, случайным образом отобранных задач, не более 20 окажутся нерешенными.
№ 51-60.
51. В партии из 8 деталей имеется 4 нестандартных. Наудачу отобрано 3 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа стандартных деталей среди отобранных.
52. Вероятность того, что деталь стандартная, равна 0,8. Проверено 4 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа стандартных деталей среди проверенных.
53. В партии из 7 деталей имеется 3 нестандартных. Наудачу отобрано 3 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди отобранных.
54. Вероятность того, что деталь стандартная, равна 0,6. Проверено 4 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди проверенных.
55. В партии из 9 деталей имеется 4 нестандартных. Наудачу отобрано 3 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди отобранных.
56. Вероятность того, что деталь стандартная, равна 0,9. Проверено 4 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа стандартных деталей среди проверенных.
57. В партии из 7 деталей имеется 4 нестандартных. Наудачу отобрано 3 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа стандартных деталей среди отобранных.
58. Вероятность того, что деталь стандартная, равна 0,7. Проверено 4 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди проверенных.
59. В партии из 10 деталей имеется 5 нестандартных. Наудачу отобрано 3 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди отобранных.
60. Вероятность того, что деталь стандартная, равна 0,75. Проверено 4 детали. Составить закон распределения, построить многоугольник распределения, найти и построить график функции распределения, найти числовые характеристики дискретной случайной величины X – числа нестандартных деталей среди проверенных.
№ 61-70.
61. Из генеральной совокупности извлечена выборка
| xi | |||||||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
62. Из генеральной совокупности извлечена выборка
| xi | [9, 11) | [11, 13) | [13, 15) | [15, 17) | [17, 19) | [19, 21) | [21, 23] |
| ni |
Построить гистограмму частот и найти числовые характеристики.
63. Из генеральной совокупности извлечена выборка
| xi | |||||||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
64. Из генеральной совокупности извлечена выборка
| xi | [7, 9) | [9, 11) | [11, 13) | [13, 15) | [15, 17) | [17, 19) | [19, 21] |
| ni |
Построить гистограмму частот и найти числовые характеристики.
65. Из генеральной совокупности извлечена выборка
| xi | |||||||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
66. Из генеральной совокупности извлечена выборка
| xi | |||||||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
67. Из генеральной совокупности извлечена выборка
| xi | [11, 14) | [14, 17) | [17, 20) | [20, 23) | [23, 26) | [26, 29) | [29, 32] |
| ni |
Построить гистограмму частот и найти числовые характеристики.
68. Из генеральной совокупности извлечена выборка
| xi | |||||||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
69. Из генеральной совокупности извлечена выборка
| xi | [15, 18) | [18, 21) | [21, 24) | [24, 27) | [27, 30) | [33, 36) | [36, 39] |
| ni |
Построить гистограмму частот и найти числовые характеристики.
70. Из генеральной совокупности извлечена выборка
| xi | 32,5 | 34,5 | 39,5 | 42,5 | |||||||
| ni |
Найти и построить эмпирическую функцию распределения, построить полигон частот. Найти точечные оценки числовых характеристик.
Примерные вопросы к экзамену
1. Предмет теории вероятностей и математической статистики. Понятия об испытаниях и событиях. Виды событий и их особенности.
2. Классическое определение вероятности. Относительные частоты. Статистическое определение вероятности. Свойства вероятности.
3. Элементы комбинаторики, основные комбинации и их формулы.
4. Несовместные события. Простые и сложные события. Теорема сложения вероятностей несовместных событий.
5. Полная группы событий, противоположные события, свойства их вероятностей.
6. Независимые события. Теорема умножения вероятностей для независимых событий.
7. Условная вероятность. Теорема умножения вероятностей зависимых событий.
8. Вероятность появления хотя бы одного события. Теорема сложения вероятностей совместных событий.
9. Формула полной вероятности. Вероятность гипотез. Формулы Байеса.
10. Повторение испытаний: формула Бернулли, наивероятнейшее число появления события.
11. Локальная теорема Лапласа. Интегральная теорема Лапласа.
12. Дискретные случайные величины: определение, закон распределения, многоугольник распределения.
13. Математическое ожидание и отклонение дискретной случайной величины, их свойства.
14. Дисперсия и среднее квадратическое отклонение дискретной случайной величины, их свойства.
15. Функция распределения вероятностей случайной величины, ее свойства и график.
16. Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Числовые характеристики НСВ.
17. Биномиальное и Пуассоновское распределения: понятие, числовые характеристики.
18. Равномерное и показательное распределения: понятие, числовые характеристики.
19. Нормальное распределение, его кривая, числовые характеристики, правило тех сигм.
20. Задачи математической статистики. Генеральная и выборочная совокупности. Виды выборки, ее репрезентативность и способы отбора.
21. Статистическое распределение выборки. Эмпирическая функция распределения. Графические представления статистических распределений (полигон и гистограмма).
22. Статистические оценки параметров распределения: несмещенные, эффективные и состоятельные оценки. Оценка генеральной средней по выборочной средней.
23. Статистические оценки параметров распределения: несмещенные, эффективные и состоятельные оценки. Генеральная и выборочная дисперсии. Оценка генеральной дисперсии по исправленной выборочной.
24. Статистическая гипотеза, статистический критерий. Нулевая и конкурирующая гипотезы. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
25. Методика отыскания теоретических частот распределения при вычислении критерия согласия Пирсона для интервальной выборки.
26. Методика отыскания теоретических частот распределения при вычислении критерия согласия Пирсона для выборки с равноотстоящими вариантами.
27. Функциональная, статистическая и корреляционная зависимости. Условные средние. Выборочное уравнение регрессии. Корреляционная таблица.
28. Выборочное уравнение регрессии в виде прямой линии. Выборочный коэффициент корреляции и его свойства.
Приложение 1
Таблица значений функции Гаусса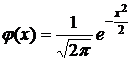 
| Цел. и десят. доли х | Сотые доли х | |||||||||
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3968 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3907 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3809 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3725 | 0,3712 | 0,3697 |
| 0,4 | 0,3677 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3514 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3324 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3114 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2888 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2651 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2410 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2169 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1933 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1705 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1489 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1287 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1102 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0934 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0784 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0651 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2,0 | 0,0536 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0436 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0352 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0281 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0222 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0174 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0134 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0103 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0078 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0059 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0032 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
Приложение 2
Таблица значений функции Лапласа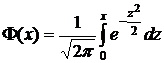 
.
| Цел. и десят. доли х | Сотые доли х | |||||||||
| 0,0 | 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 |
| 0,1 | 0,0398 | 0,0438 | 0,0478 | 0,0517 | 0,0557 | 0,0596 | 0,0636 | 0,0675 | 0,0714 | 0,0753 |
| 0,2 | 0,0793 | 0,0832 | 0,0871 | 0,0910 | 0,0948 | 0,0987 | 0,1026 | 0,1064 | 0,1103 | 0,1141 |
| 0,3 | 0,1179 | 0,1217 | 0,1255 | 0,1293 | 0,1331 | 0,1368 | 0,1406 | 0,1443 | 0,1480 | 0,1517 |
| 0,4 | 0,1554 | 0,1591 | 0,1628 | 0,1664 | 0,1700 | 0,1736 | 0,1772 | 0,1808 | 0,1844 | 0,1879 |
| 0,5 | 0,1915 | 0,1950 | 0,1985 | 0,2019 | 0,2054 | 0,2088 | 0,2123 | 0,2157 | 0,2190 | 0,2224 |
| 0,6 | 0,2257 | 0,2291 | 0,2324 | 0,2357 | 0,2389 | 0,2422 | 0,2454 | 0,2486 | 0,2517 | 0,2549 |
| 0,7 | 0,2580 | 0,2611 | 0,2642 | 0,2673 | 0,2704 | 0,2734 | 0,2764 | 0,2794 | 0,2823 | 0,2852 |
| 0,8 | 0,2881 | 0,2910 | 0,2939 | 0,2967 | 0,2995 | 0,3023 | 0,3051 | 0,3078 | 0,3106 | 0,3133 |
| 0,9 | 0,3159 | 0,3186 | 0,3212 | 0,3238 | 0,3264 | 0,3289 | 0,3315 | 0,3340 | 0,3365 | 0,3389 |
| 1,0 | 0,3413 | 0,3438 | 0,3461 | 0,3485 | 0,3508 | 0,3531 | 0,3554 | 0,3577 | 0,3599 | 0,3621 |
| 1,1 | 0,3643 | 0,3665 | 0,3686 | 0,3708 | 0,3729 | 0,3749 | 0,3770 | 0,3790 | 0,3810 | 0,3830 |
| 1,2 | 0,3849 | 0,3869 | 0,3888 | 0,3907 | 0,3925 | 0,3944 | 0,3962 | 0,3980 | 0,3997 | 0,4015 |
| 1,3 | 0,4032 | 0,4049 | 0,4066 | 0,4082 | 0,4099 | 0,4115 | 0,4131 | 0,4147 | 0,4162 | 0,4177 |
| 1,4 | 0,4192 | 0,4207 | 0,4222 | 0,4236 | 0,4251 | 0,4265 | 0,4279 | 0,4292 | 0,4306 | 0,4319 |
| 1,5 | 0,4332 | 0,4345 | 0,4357 | 0,4370 | 0,4382 | 0,4394 | 0,4406 | 0,4418 | 0,4429 | 0,4441 |
| 1,6 | 0,4452 | 0,4463 | 0,4474 | 0,4484 | 0,4495 | 0,4505 | 0,4515 | 0,4525 | 0,4535 | 0,4545 |
| 1,7 | 0,4554 | 0,4564 | 0,4573 | 0,4582 | 0,4591 | 0,4599 | 0,4608 | 0,4616 | 0,4625 | 0,4633 |
| 1,8 | 0,4641 | 0,4649 | 0,4656 | 0,4664 | 0,4671 | 0,4678 | 0,4686 | 0,4693 | 0,4699 | 0,4706 |
| 1,9 | 0,4713 | 0,4719 | 0,4726 | 0,4732 | 0,4738 | 0,4744 | 0,4750 | 0,4756 | 0,4761 | 0,4767 |
| 2,0 | 0,4772 | 0,4778 | 0,4783 | 0,4788 | 0,4793 | 0,4798 | 0,4803 | 0,4808 | 0,4812 | 0,4817 |