Ряды распределения и приемы их построения

Различия индивидуальных значений признака у единиц совокупности называются вариацией признака. Она возникает в результате того, что индивидуальные значения складываются под совместным влиянием разнообразных условий (факторов), по разному сочетающихся в каждом отдельном случае.

Изучение вариации в пределах однородной группы предполагает использование следующих приемов: построение вариационного ряда (ряда распределения), его графическое изображение, исчисление основных характеристик распределения.

Вариационный ряд – групповая таблица, построенная по количественному признаку, в сказуемом которой показывается число единиц в каждой группе. Форма построения вариационного ряда зависит от характера изменения изучаемого признака, он может быть построен в форме дискретного или интервального ряда.

По характеру вариации значений признака различают:

- признаки с прерывным изменением (дискретные);

- признаки с непрерывным изменением (непрерывные).

Признаки с прерывным изменением могут принимать лишь конечное число определенных значений (например, тарифный разряд рабочих). Признаки с непрерывным изменением могут принимать в определенных границах любые значения (например, пробег автомобиля).

Для признака, имеющего прерывное изменение и принимающего небольшое количество значений, применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе – численность единиц с определенным значением признака.

Для признака, имеющего непрерывное изменение, строится интервальный вариационный ряд, состоящий, так же как и дискретный ряд, из двух граф (варианты и частоты). При его построении в первой графе отдельные значения признака указываются в интервалах «от - до», во второй графе – число единиц, входящих в интервал. Интервалы образуются, как правило, равные и закрытые.

Вариационный ряд, состоящий из двух граф (варианты и частоты), иногда дополняются другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S). Накопленные частотыпоказывают, сколько единиц совокупности имеют значения признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму, т.е.

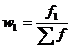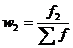; и т.д. (5.3)

Если вариационный ряд дан с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчет абсолютной или относительной плотности распределения.

Абсолютная плотность распределения(p) представляет собой величину частоты, приходящейся на единицу размера интервала отдельной группы ряда: p = f / i. (5.4)

Относительная плотность распределения(p^/) – частное от деления частости (w) отдельной группы на размер ее интервала: p^/ = w / i . (5.5)

Следующим этапом изучения вариационного ряда является его графическое изображение.

Для наглядного представления вариационных рядов используют графические методы: полигоны распределения частот, гистограммы частот, кумулятивные кривые и т.п. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности.

Полигон — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — частоты.

Гладкая кривая, соединяющая точки, — эмпирическая плотность распределения.

Кумулята — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — накопленные частоты.

Для дискретных рядов на оси откладываются сами значения признака, а для интервальных — середины интервалов.

Дискретный вариационный ряд изображается в виде полигона распределения частот. Для изображения интервального ряда применяются полигоны распределения частот и гистограмма частот. В ряде случаев для изображения вариационных рядов используются кумулятивная кривая (кумулята) и огива.

Для анализа вариационных рядов используются три группы показателей:

- показатели центра распределения;

- показатели степени вариации;

- показатели формы распределения.