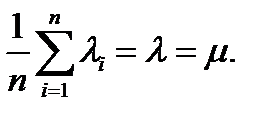Понятие о ПГР, стационарное решение и его интерпретация

Определение.

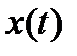- дискретный случайный процесс (с.п.) ( ).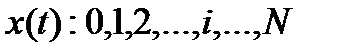

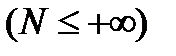Пусть T – произвольный момент времени;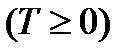

Пусть ; .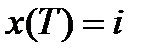

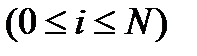За время 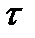( 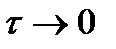) процесс переходит в состояние:

а) 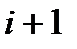с вероятностью ( )

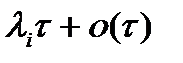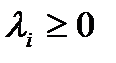б) 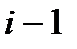с вероятностью ( )

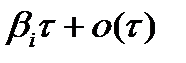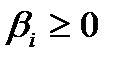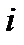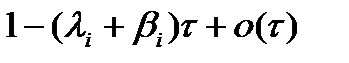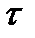в) с вероятностью , 0( )-б.м. величина.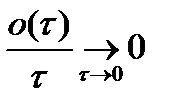

Если для с.п. выполн. эти усл., он наз. ПГР (процесс гибели и размножения) и он не зависит от прошлого состояния.

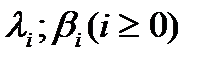- параметры процесса, не зависящие от времени, от прошлых состояний системы.

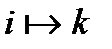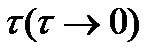Вероятность перехода за равна 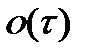, если 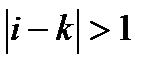. Невозможность перехода в более низкие состояния.

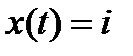- значит, что численность популяции в момент 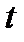равна .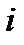

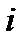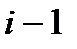, (гибель) и (размножение)– три существенных (наиб. вероят.) сост. при переходе из 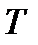в .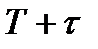

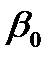для любого ПГР равно 0.

Если 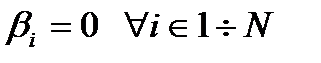(частный случай), это процесс (чистого) размножения (ПР).

Если 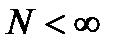, то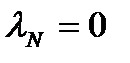

Частный случай: когда при этом ещё и .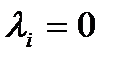

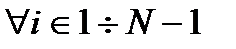Крайний частный случай: Если 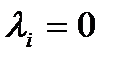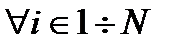, либо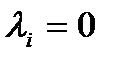 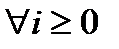(для случая 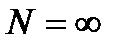) – это процесс гибели (ПГ). Невозможен переход в более высокие состояния.

Постановка задачи Эрланга для ПГГ

- ПГР, сл.пр. дискретн.. - вер-ть того, что в мом. в СО выз.

Нахождение мн-ва ф-ций - задача Эрланга

Свойства :

1. Неотрицательность: ;
2. Нормировочное условие: , если N<

Если , - взрыв (бесконеч. сост-е) невозмож.

Пусть .

- начальные вероятности (исходные данные, известны). Это вер. В 0-й момент времени.

Требуется найти: закон распр-я вер-тей на любой последующий момент времени.

Каждая зависит от

;

1. ; ;

Решается задача Эрланга в предельной форме: ?

Нахождение ( ) - задача Эрланга в предельной форме - задача нахождения стационарного решения.

Свойства :

1. Неотрицательность: ;

2. Нормировочные условия:

Можно показать, что (без док-ва). Рекур.соотн.

- ?

. Пусть правое слагаемое меньше , если //при тоже//. Тогда

След. ( ).

Интерпретация :

- вероятность -го состояния, (ровно вызовов в системе).

T

- время пребывания СО в состоянии .

- среднее относительное время пребывания СО в состоянии (доля времени, в течение которого в СО вызовов).

Теорема :

, то есть

- среднее относительное время пребывания процесса в состоянии . Если - большое, то - средняя длина промежутка времени, в течение которого в системе было ровно вызовов.

Задание потока вызовов

Существует 2 способа задания потока вызовов:

· Случайный процесс;

· Последовательность случайных величин.

Способ 1:

Поток вызовов как случайный процесс.

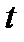- произвольный момент времени; .

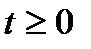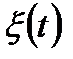- число вызовов, поступивших в промежутке 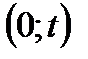.Если 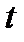меняется, то 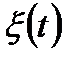- семейство случайных величин, зависящих от 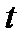- случайный процесс.

Свойства :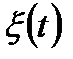

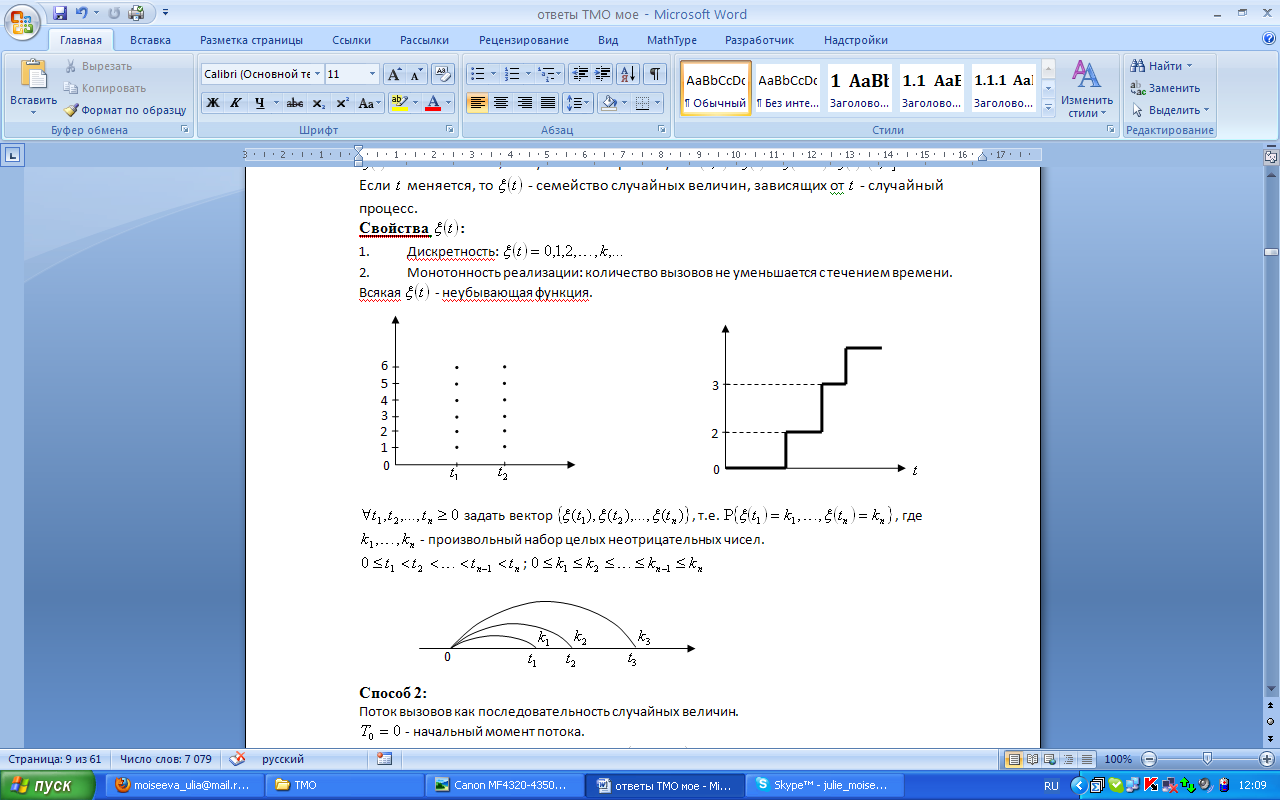
1. Дискретность: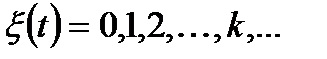

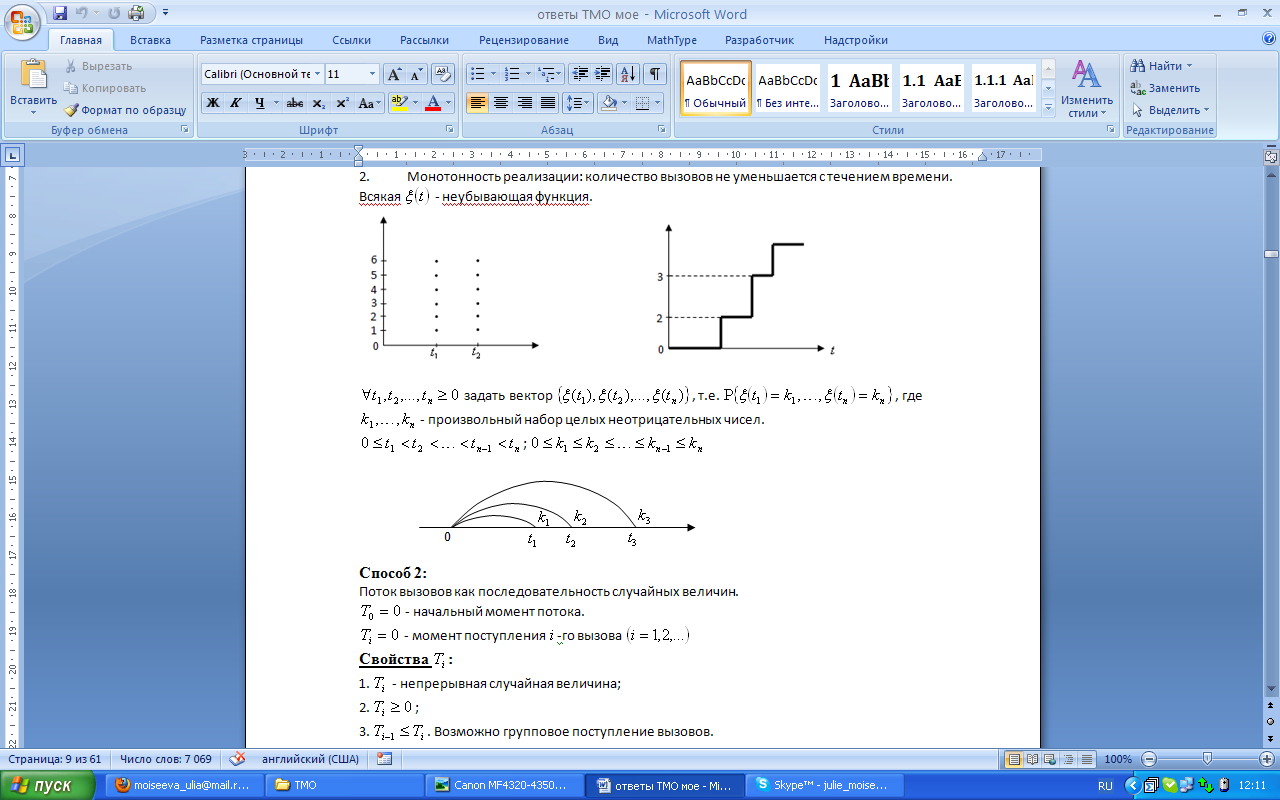
2. Монотонность реализации: количество вызовов не уменьшается с течением времени. Всякая 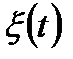- неубывающая функция.

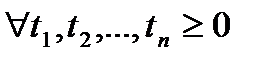задать вектор 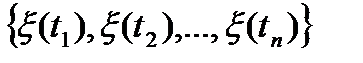, т.е. 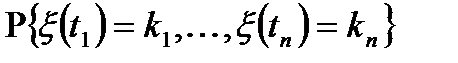, где 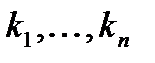- целые неотрицательные числа. Вер.отлична от 0, если:

;

Способ 2:

Поток вызовов как последовательность случайных величин.

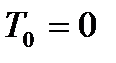- начальный момент потока.

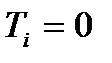- момент поступления 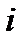-го вызова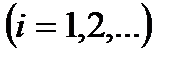

Свойства :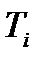

1. 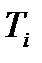- непрерывная случайная величина; ;

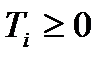2. 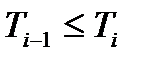. Возможно групповое поступление вызовов.

Пусть 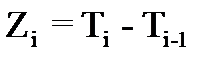, где i>1, тогда 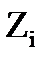- длина промежутка времени между моментами поступления i-1 и i вызова. 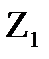– от начального момента потока до поступления первого вызова.

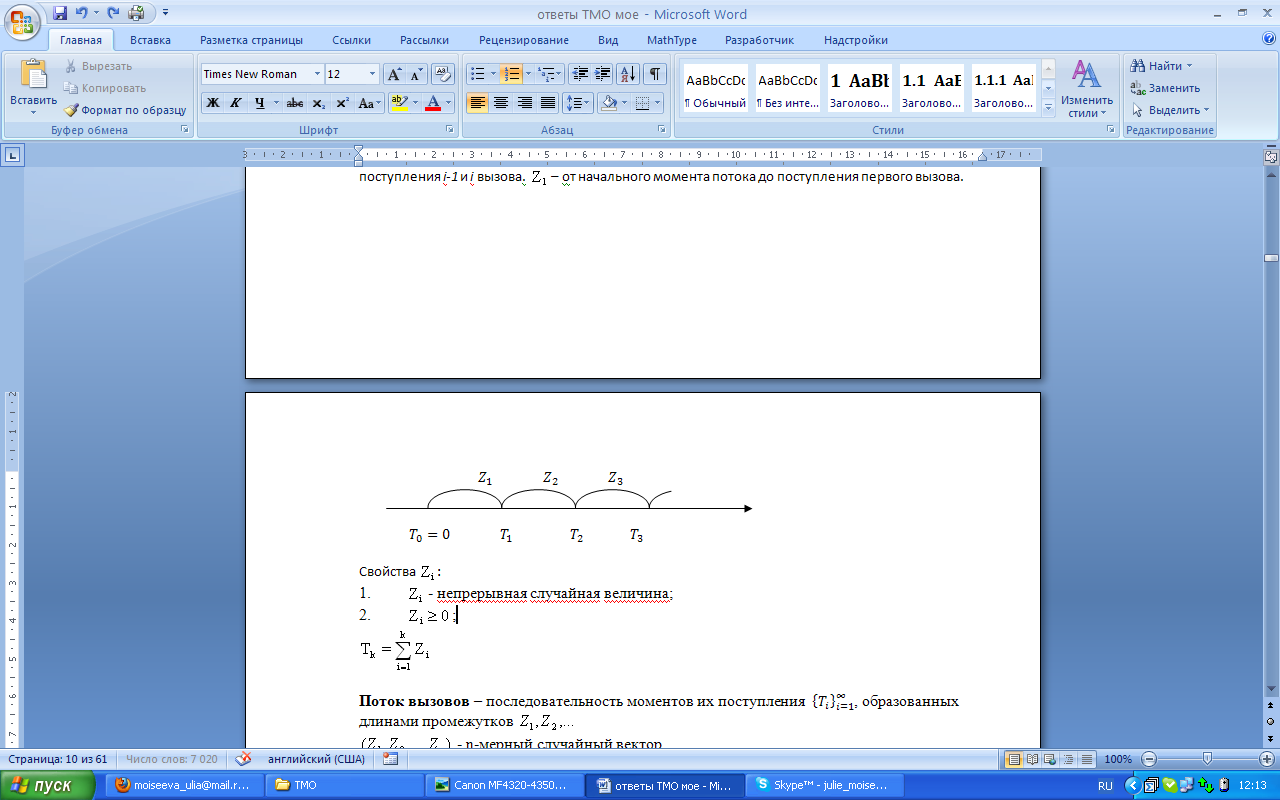Свойства :

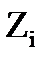1. 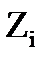- непрерывная случайная величина;

2. ;

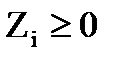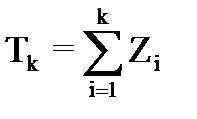
Поток вызовов – последовательность моментов поступления вызовов, образованных длинами промежутков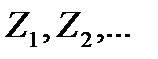

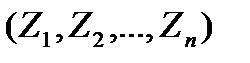- n-мерный случайный вектор.

Поток задан, если известна функция распределения такого вектора:

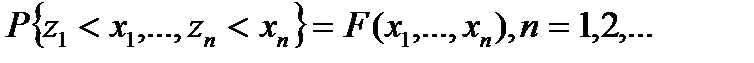, где все Хксы положительные.

Оба способа задания потока равносильны.

Простейший поток вызовов

Поток вызовов – с.п.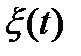

Первое определение простейшего потока:

Поток вызовов называется простейшим, если выполняются 3 условия:

1. 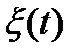- марковский;

2. Вероятность поступления ровно k вызовов в промежутке времени длиной t не зависит от начального момента этого промежутка (условие стационарности);

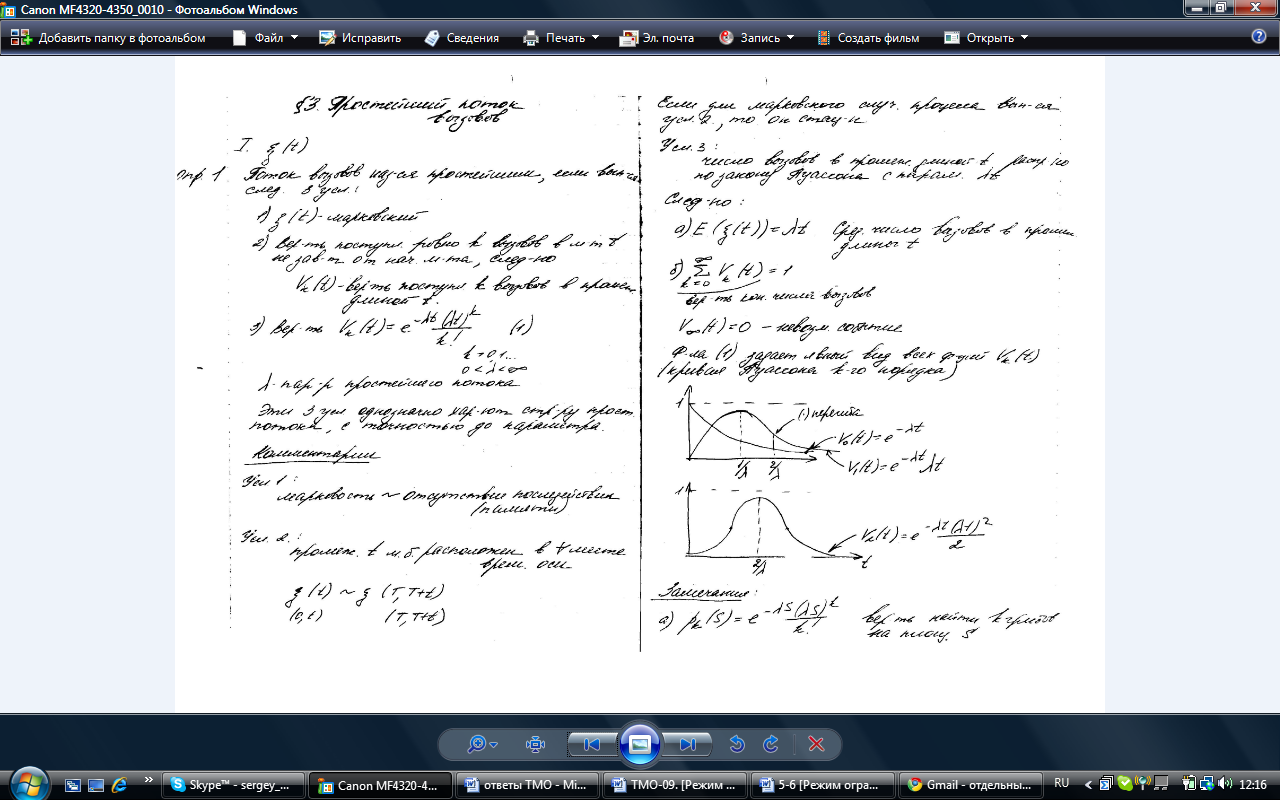
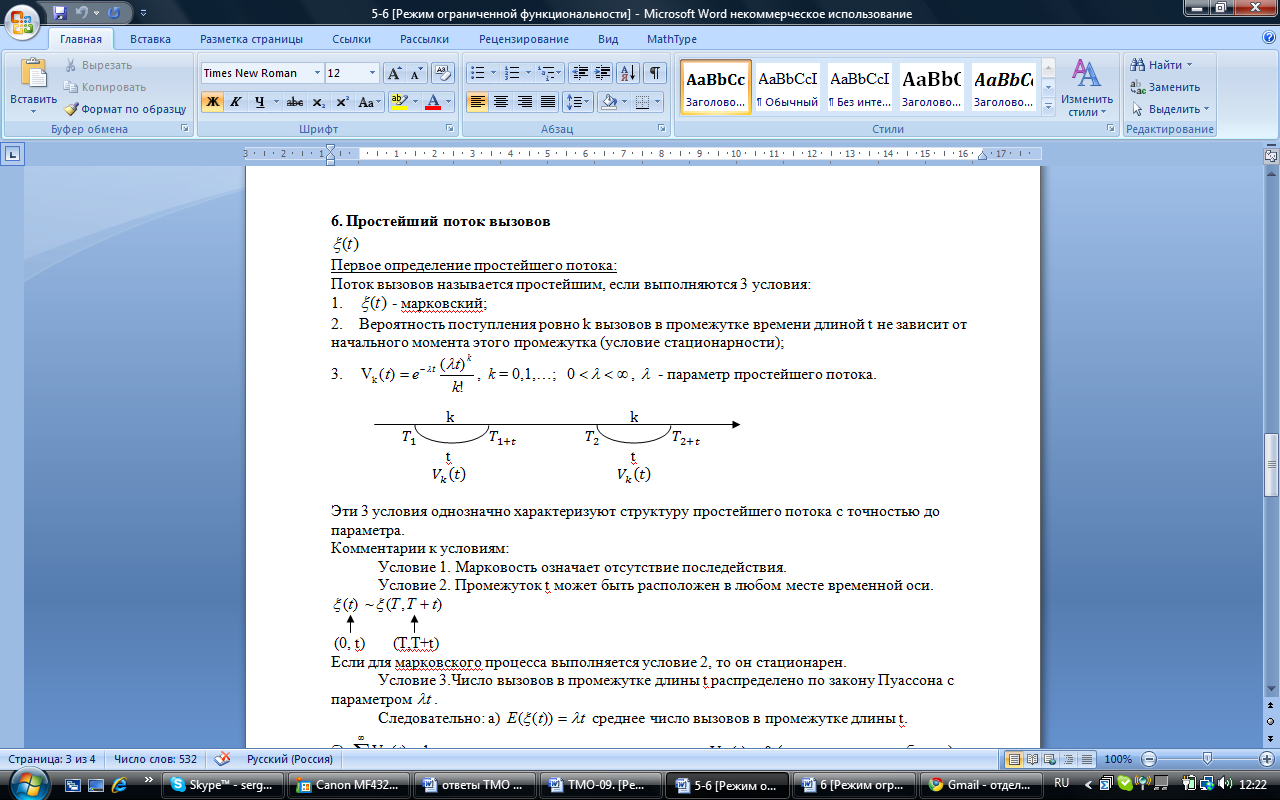
3. 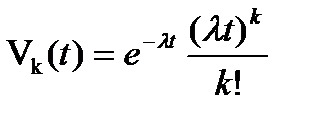, k = 0,1,…; 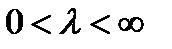, 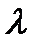- параметр простейшего потока.

Эти 3 условия однозначно характеризуют структуру простейшего потока с точностью до параметра .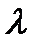

Комментарии к условиям:

Условие 1. Марковость означает отсутствие последействия.

Условие 2. Промежуток t может быть расположен в любом месте временной оси.

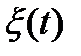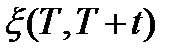~ -равносильны, один и тот же закон распределения.

Если для марковского процесса выполняется условие 2, то он стационарен.

Условие 3.Число вызовов в промежутке длины t распределено по закону Пуассона с параметром .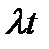

Следовательно: а) 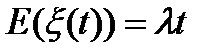среднее число вызовов в промежутке длины t.Коэф.пропор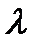

б) 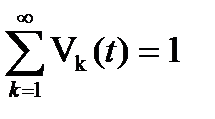вероятность конечного числа вызовов; 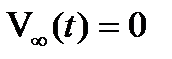(невозможность события)

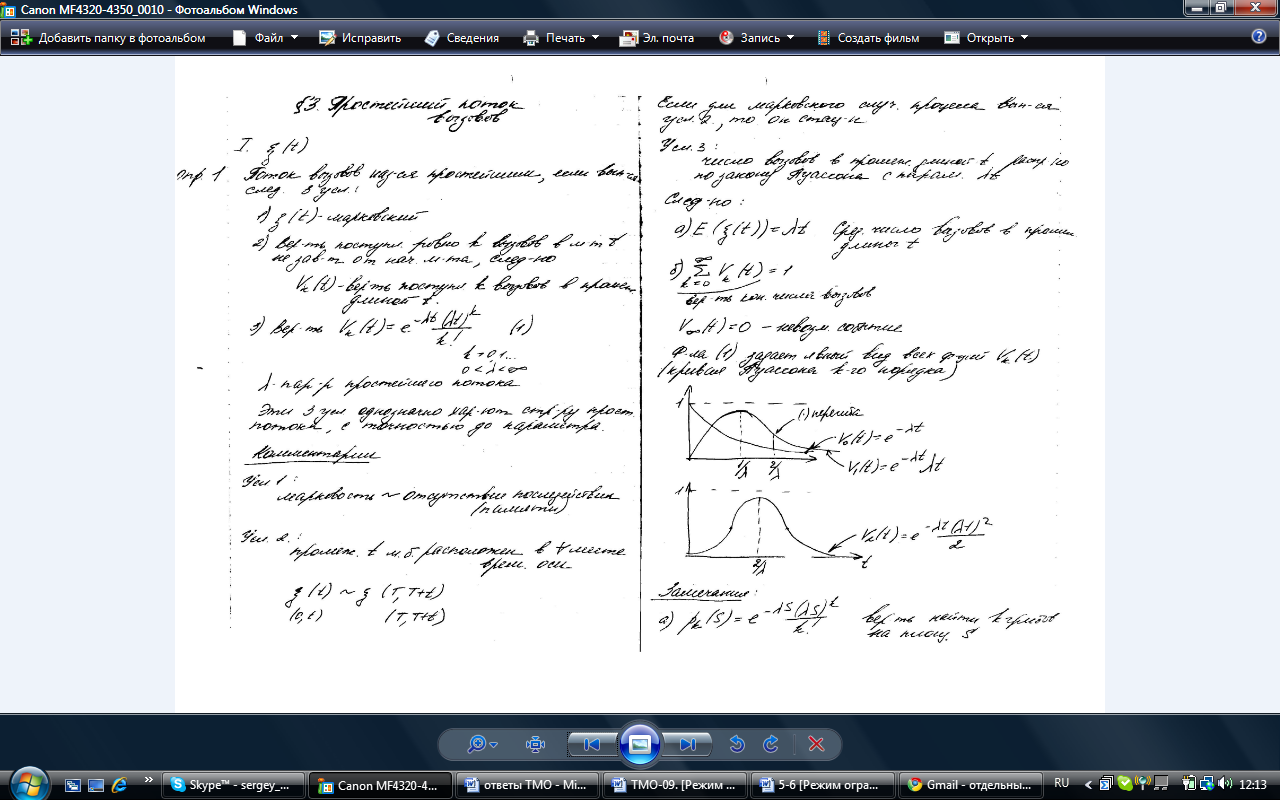
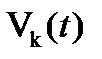– Кривая Пуассона 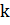-го порядка.

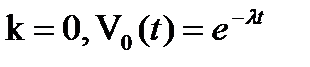
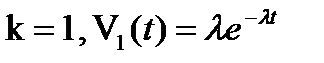
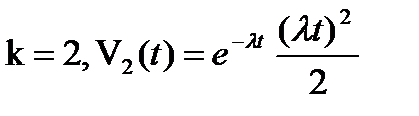
Два простейших потока могут

отличаться

друг от друга только значением

параметра.

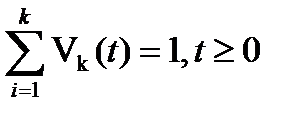
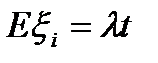
Интенсивностью 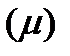стационарного потока называется среднее число вызовов, поступающих за промежуток времени единичной длины .

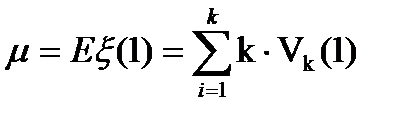Применение: Среднее число вызовов в промежутке пропорционально длине этого промежутка, причем 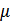является коэффициентом пропорциональности.

Доказательство: Пусть 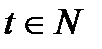, разобьем на промежутки единичной длины: рисуем.

1.

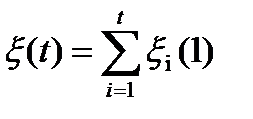
2.

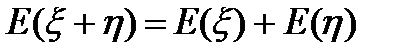
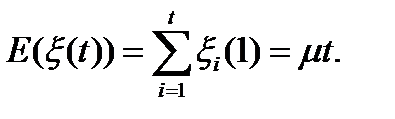ч. т. д.

Свойства простейшего потока:

A)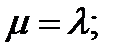

Доказательство 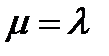(2 варианнта):

1.

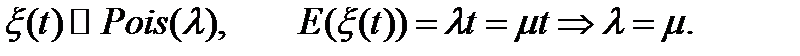
B) Средняя длина промежутка между последовательными вызовами равна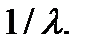

( )

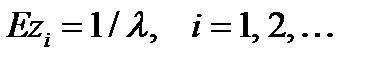Расчет 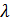или 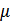для простейшего потока:

1. Наблюдаем за случайной величиной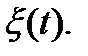

2. Регистрируем реальные значения этой величины: 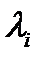―результат iого наблюдения (в iый промежуток ед. длины)

3. Среднее арифметическое этих наблюдений: