Сведения из теории вероятностей
О задачах ТМО
ТМО – важная ветвь современной теории вероятности. Эта теория может быть использована для наиболее экономного проектирования любых систем, предназначенных для удовлетворения массового потока каких-либо заявок случайного характера. Эрланг – основатель.
| n линий связи АТС СО |
| АТС |
| Поток вызовов (входящий поток) |
Часто в качестве системы обслуживания (СО) рассматривалась АТС.
Количество линий связи конечно. Количество вызовов и длины разговоров – случайные величины.
Если 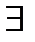 свободная линия, то поступивший вызов ее занимает. Если в момент поступления вызова все линии заняты, то его дальнейшая «участь» зависит от типа СО.
свободная линия, то поступивший вызов ее занимает. Если в момент поступления вызова все линии заняты, то его дальнейшая «участь» зависит от типа СО.
Типы СО:
1. СО с отказом (потерей). Система, кот. Теряет клиентов.
2. СО с ожиданием (вызов становится в очередь)
3. Смешанные СО (пример: системы с ограниченной очередью (числом мест ожидания), m – максимально допустимый размер очереди. Вызов ставится в очередь, если длина очереди меньше m, получает отказ, если равно m).
4. Бесконечный пучок ( n= 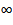 , нет ни отказов, ни ожиданий, возможно в теории)
, нет ни отказов, ни ожиданий, возможно в теории)
Основные задачи ТМО:
1. Нахождение стационарного решения - вероятностей отдельных состояний СО в установившемся режиме независимо от времени.
Состояние СО на момент времени t: 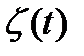 .
.
-количество вызовов в СО на момент t
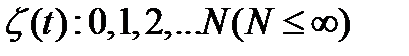
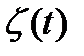 - случайный процесс.
- случайный процесс.
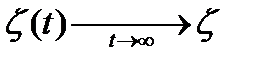 - случайная величина, стационарный процесс.
- случайная величина, стационарный процесс.
2. Расчет показателей эффективности функционирования данной СО.
Показатели:
-абсолютные (1.универсальные, 2.специфические)
-относительные (средняя доля абсолютного показателя) Кобс,Кзагр.
Для СО с отказом основным показателем является 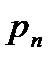 (вероятность отказа(потерь), вероятность застать все линии занятыми(полной загрузки)).
(вероятность отказа(потерь), вероятность застать все линии занятыми(полной загрузки)).
Для СО с ожиданием - 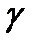 - время ожидания обслуживания (время очереди) (непрыревная,
- время ожидания обслуживания (время очереди) (непрыревная, 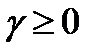 ). Функция распределения
). Функция распределения 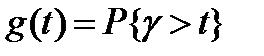 . Показатель эффективности
. Показатель эффективности 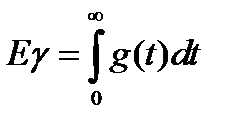 - среднее время ожидания обслуживания. Для дискретной случайной величины:
- среднее время ожидания обслуживания. Для дискретной случайной величины: 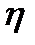 -длина очереди
-длина очереди 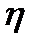 : 0,1,2…).Вероятности р0,р1,р2,…Суммар=1.
: 0,1,2…).Вероятности р0,р1,р2,…Суммар=1. 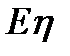 - средняя длина очереди.
- средняя длина очереди.
Для смешанных СО - 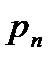 ,
, 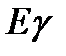 ,
, 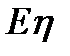 .
.
3. В СО, ищется система,кот. Обслуживает поток поступающих вызовов, т.е. очередь ведет себя естественным образом (не растет до бесконечности, она колеблется), т.е. СО справляется с обслуживанием.
4. Расчет рационального числа линий (n) в данной СО. 2 точки зрения:
а) С точки зрения входящего потока, с отказом 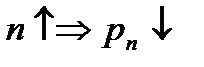
с ожиданием 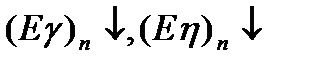
б) с т. зрения самой СО n не должно быть чрезмерно большим , так как большие затраты, а Кзагр уменьшается 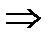 необходим поиск «золотой середины», чтобы показатели эфф-ти СО были наилучшими.
необходим поиск «золотой середины», чтобы показатели эфф-ти СО были наилучшими.
Примеры: 1.расчет числа продавцов или касс в торговых предприятиях
1. расчет числа причалов в порту, посадочных полос на аэродроме
2. расчет количества оборонительных средств
3. расчет запаса товара в магазине для бесперебойн. снабжения насел. этим тов.
4. Расчет размера запаса товара в магазине
Области применения ТМО
- экономика и организация производства. 2. Транспорт. 3. Техника (теория надежности). 4. военное дело. 5. естествознание (ядерная физика, биология).
I. Показательный закон
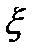 - с.в., непр., >0.
- с.в., непр., >0. 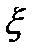 распределена так, что ее распределение имеет показательный вид:
распределена так, что ее распределение имеет показательный вид:
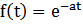 , 0<a<
, 0<a< 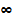 , a – параметр показательного закона
, a – параметр показательного закона
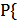
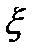 >t}=
>t}= 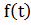

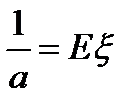
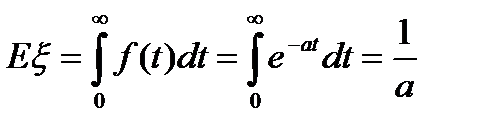
с т.з. мат.анализа «а» – темп убывания 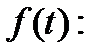
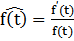 ,
, 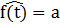 ó
ó 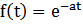
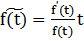 -эластичность функции f(t)
-эластичность функции f(t)
А) 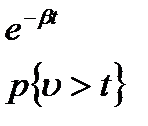 1/в-средняя длина разговора
1/в-средняя длина разговора
Б)|-------------|---------------|----- Zi-длина промежутка времени
z1 T1 z2 T2 z3
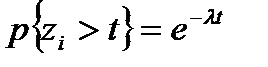
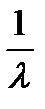 -средняя длина промежутка между вызовами
-средняя длина промежутка между вызовами
II. Закон Пуассона
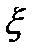 : 0,1,2...,k,…
: 0,1,2...,k,…
Сл. вел 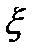 - распределена по закону Пуассона, если
- распределена по закону Пуассона, если
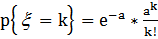 , k=0,1,2,…
, k=0,1,2,…
0<a< 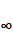 , a – параметр
, a – параметр
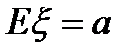
III. Биномиальный закон
n –количество независимых испытаний с двумя исходами в каждом испытании (успех p,не удача:1-p
p – вероятность успеха
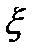 - количество успехов в серии из n испытаний,
- количество успехов в серии из n испытаний, 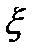 :0,1,2,…n, то
:0,1,2,…n, то 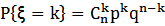 .
.
Понятие о случайном процессе и его задании
t - вещественное неотр.число
Если t – фиксир, то x(t) –с.в.; если t меняется, то x(t) – c.п. (с.ф.)-семейство
С.п. x(t) - 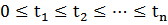 (n=1,2,..)
(n=1,2,..)
Известен закон распределения
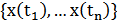 - n-мерный случайный вектор (1)
- n-мерный случайный вектор (1)
Дискретная с.п.
В ТМО x(t):0,1,2,3,..i,…,N, ( 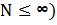
x(t) – дискр с.п.
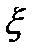 (t)-число вызовов, поступающих в (0,t)
(t)-число вызовов, поступающих в (0,t)
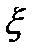 (t):0,1,2…..i…..
(t):0,1,2…..i…..
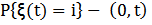 i вызов
i вызов
S(t) – монотонно неубыв. функция
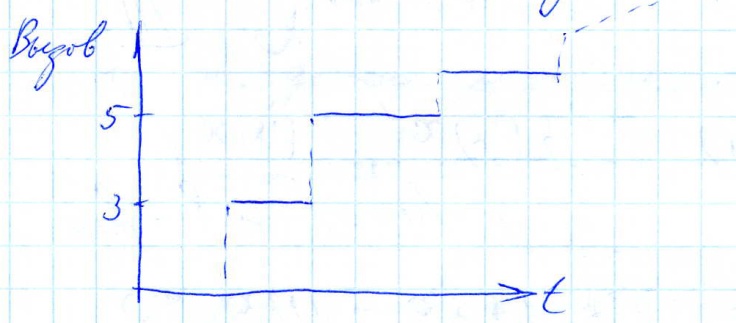 Реализация случайного процесса
Реализация случайного процесса 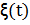 -лестница
-лестница
2. 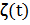 - состояние (число вызовов) в СО на t.
- состояние (число вызовов) в СО на t.
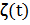 : 0,1,2,3,..i,…,N, (
: 0,1,2,3,..i,…,N, ( 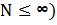
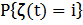 - вероятность того, что в момент t в СО находится i вызовов.
- вероятность того, что в момент t в СО находится i вызовов.
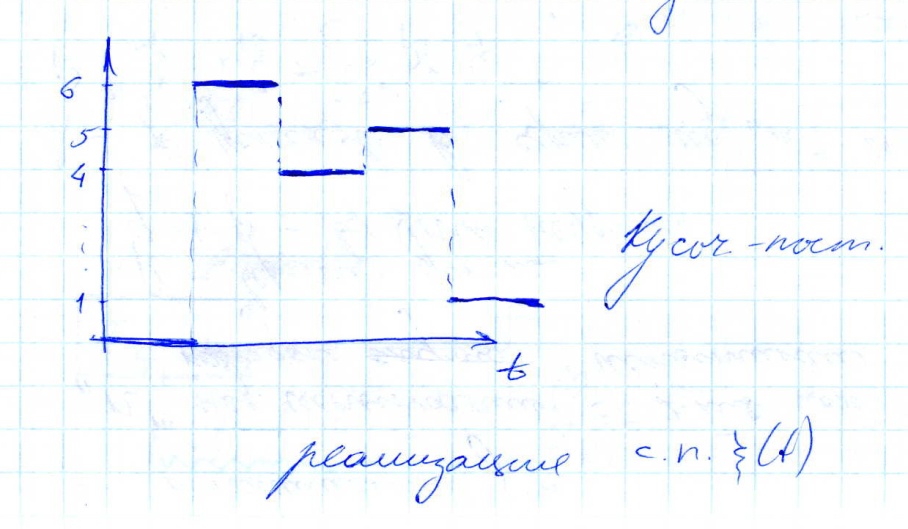 Реализация с.п.
Реализация с.п. 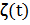
x(t)- дискр. с.п.
x(t):0,1,2,3,..i,…,N, ( 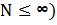
вектор (1)
Ф.р. 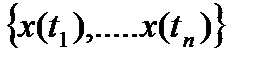
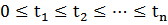 (n=1,2,..)
(n=1,2,..)
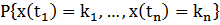 ,
, 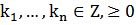 -функция распределения вектора (1), К-нат.числа
-функция распределения вектора (1), К-нат.числа
Марковские с.п.
x(t) – дискр с.п., x(t):0,1,2,…,N
T – любой момент времени фиксированный, 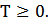
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 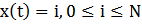 ,
,
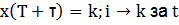 .
.
Марковский с.п. – с.п. x(t): вероятность перехода из состояния i в состояние k за  не зависит от прошлого течения процесса, т.е. от сотояния до T. Будущее не зависит от прошлого, а только от настоящего.
не зависит от прошлого течения процесса, т.е. от сотояния до T. Будущее не зависит от прошлого, а только от настоящего.
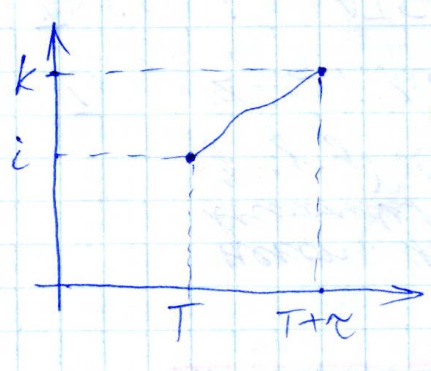
Переходная вероятность:  ,
, 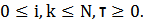
С.п. x(t)-марковский сл.процесс (процесс без последействий, без памяти).
Основные понятия и допущения в ТМО
Система массового обслуживания (СО) – организация, которая может выполнять работу (предоставлять услугу) одного вида. Пр.: АТС, магазин, порт, аэродром.
Вызов (требование) – заявка на выполнение работы (предоставление услуги), на которую способна данная система.
Поток вызовов делится на: входящий и выходящий.
Входящий поток вызовов - вызовы, поступающие в данную СО и нуждающиеся в услуге, на которую способна данная СО. Целесообразно разделить на:
1)для систем с отказом(кому повезло, кому не повезло)
2)для систем с ожидан. (принятые сразу, ожидающие)
Выходящий поток – вызовы, покидающие данную СО. Для систем, где существуют отказы, он распадается на поток обслуженных вызовов и поток отказов.
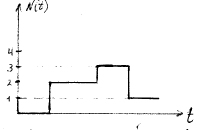 Состояние СО – количество вызовов, имеющихся в СО на тот или иной момент времени
Состояние СО – количество вызовов, имеющихся в СО на тот или иной момент времени 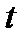 , принимает значения
, принимает значения 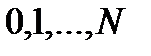 (
( 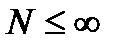 ).
).
// У Алипова 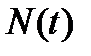 - так на картинке. У нас это
- так на картинке. У нас это 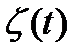 //
//
1. Состояния СО по 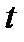 :
: 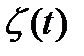 - случ. процесс (с.п.);
- случ. процесс (с.п.);
- Состояние в стационарном решении:
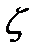 - случайная величина (с.в.),
- случайная величина (с.в.), 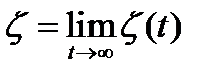 .
.
Линия –обслуживающий прибор, который выполняет работу данного вида. Пр. линий: продавец, парикмахер, причал (док), почтальон.
Пучок линий – совокупность всех линий в СО
Виды линий:
. Он конечный, если 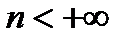 (
( 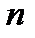 - количество линий в пучке), бесконечный – в противном случае.
- количество линий в пучке), бесконечный – в противном случае.
Пучок линий полнодоступный, если любой поступающий вызов может попасть на любую линию. (все линии взаимозаменяемые).
Пучок линий упорядоченный, если все линии пронумерованы, и вызов занимает линию с наименьшим номером из числа свободных линий.
Разговор (длина разговора) - 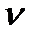 - время обслуживания на любой линии. Время обслуживание считается одинаковой.
- время обслуживания на любой линии. Время обслуживание считается одинаковой. 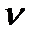 - непрер. случайная величина,
- непрер. случайная величина, 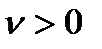 , функция распределения
, функция распределения 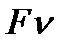 считается известной.
считается известной.
Функция распределения: 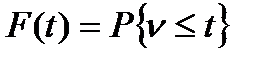 ,
, 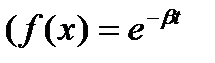
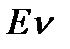 - средняя длина разговора =
- средняя длина разговора = 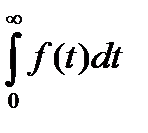
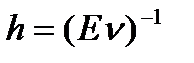 - интенсивность обслуж-я вызовов на линии - пропускная спос-ть линии (номинальная) - сред. число выз., кот. мож. обслуж. кажд. линия за ед. вр..
- интенсивность обслуж-я вызовов на линии - пропускная спос-ть линии (номинальная) - сред. число выз., кот. мож. обслуж. кажд. линия за ед. вр..
nh- пропускная способность СО.
nht- среднее число вызовов.
Допущения в ТМО:
1. Кажд. вызов обслуж-ся только одной линией (индивидуальное обслуж-е). Противоположное: групповое обслуживание.
2. Кажд. линия в любой данный момент обслуживает не более одного вызова
3. Любой начатый разговор не прерывается вплоть до его завершения (полное обслуживание). Противоположное – частичное обслуживание.
4. Длины разговоров (работа линий) не зависят от вход. потока и друг от др.
5. СО, где допускаются очереди (СОЖ или смешанные), предполагает обслуживание в порядке очереди - т.о., нет приоритетных вызовов.
Определение.
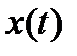 - дискретный случайный процесс (с.п.) (
- дискретный случайный процесс (с.п.) ( 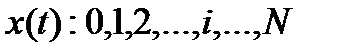
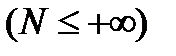 ).
).
Пусть T – произвольный момент времени; 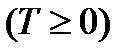
Пусть 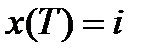 ;
; 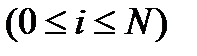 .
.
За время 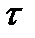 (
( 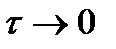 ) процесс переходит в состояние:
) процесс переходит в состояние:
а) 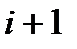 с вероятностью
с вероятностью 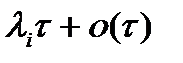 (
( 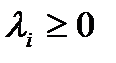 )
)
б) 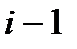 с вероятностью
с вероятностью 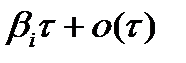 (
( 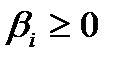 )
)
в) 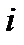 с вероятностью
с вероятностью 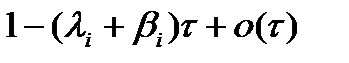 , 0(
, 0( 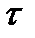 )-б.м. величина.
)-б.м. величина. 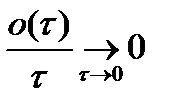
Если для с.п. выполн. эти усл., он наз. ПГР (процесс гибели и размножения) и он не зависит от прошлого состояния.
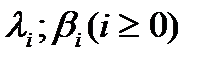 - параметры процесса, не зависящие от времени, от прошлых состояний системы.
- параметры процесса, не зависящие от времени, от прошлых состояний системы.

Вероятность перехода 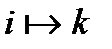 за
за 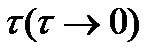 равна
равна 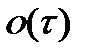 , если
, если 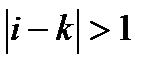 . Невозможность перехода в более низкие состояния.
. Невозможность перехода в более низкие состояния.
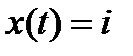 - значит, что численность популяции в момент
- значит, что численность популяции в момент 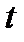 равна
равна 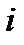 .
.
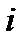 ,
, 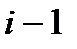 (гибель) и
(гибель) и  (размножение)– три существенных (наиб. вероят.) сост. при переходе из
(размножение)– три существенных (наиб. вероят.) сост. при переходе из 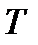 в
в 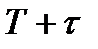 .
.
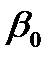 для любого ПГР равно 0.
для любого ПГР равно 0.
Если 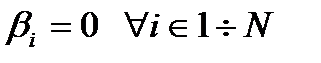 (частный случай), это процесс (чистого) размножения (ПР).
(частный случай), это процесс (чистого) размножения (ПР).
Если 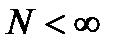 , то
, то 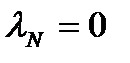
Частный случай: когда при этом ещё и 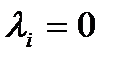
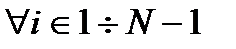 .
.
Крайний частный случай: Если 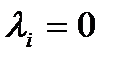
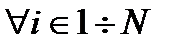 , либо
, либо 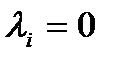
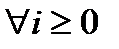 (для случая
(для случая 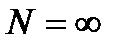 ) – это процесс гибели (ПГ). Невозможен переход в более высокие состояния.
) – это процесс гибели (ПГ). Невозможен переход в более высокие состояния.
Задание потока вызовов
Существует 2 способа задания потока вызовов:
· Случайный процесс;
· Последовательность случайных величин.
Способ 1:
Поток вызовов как случайный процесс.
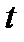 - произвольный момент времени;
- произвольный момент времени; 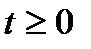 .
.
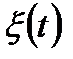 - число вызовов, поступивших в промежутке
- число вызовов, поступивших в промежутке 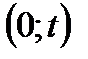 .Если
.Если 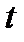 меняется, то
меняется, то 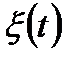 - семейство случайных величин, зависящих от
- семейство случайных величин, зависящих от 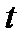 - случайный процесс.
- случайный процесс.
Свойства 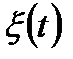 :
:
1. Дискретность: 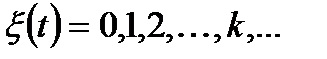
2. Монотонность реализации: количество вызовов не уменьшается с течением времени. Всякая 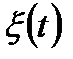 - неубывающая функция.
- неубывающая функция.
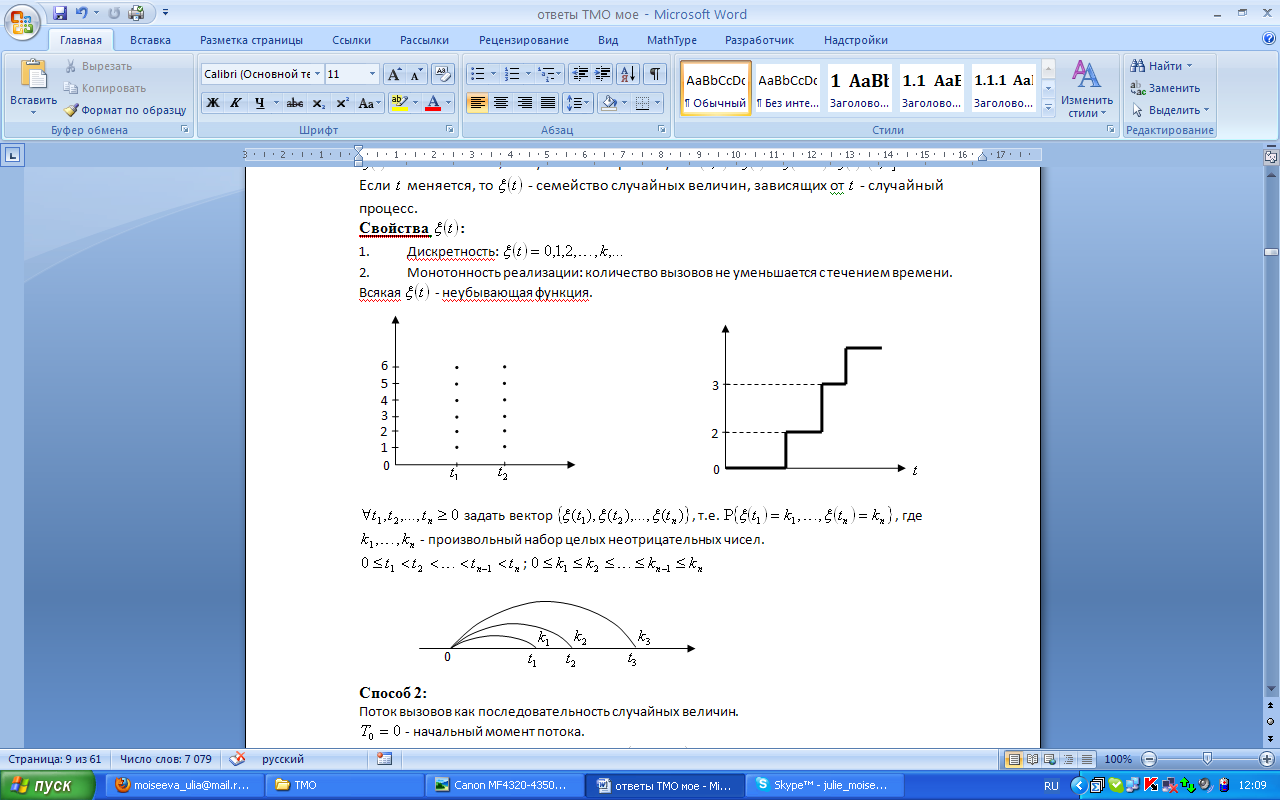
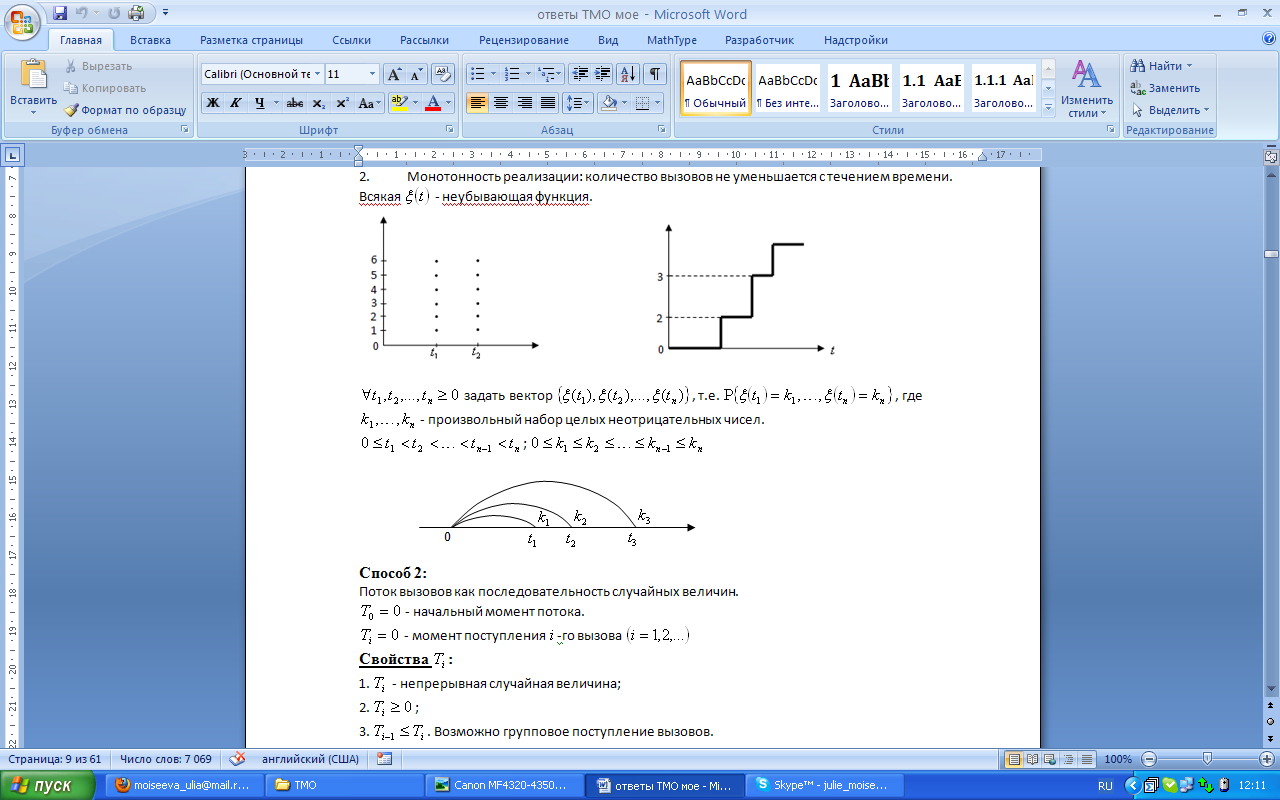
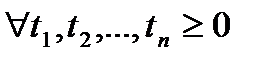 задать вектор
задать вектор 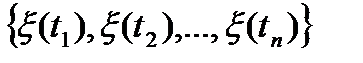 , т.е.
, т.е. 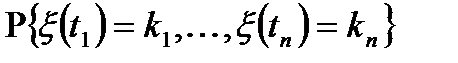 , где
, где 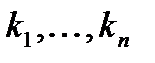 - целые неотрицательные числа. Вер.отлична от 0, если:
- целые неотрицательные числа. Вер.отлична от 0, если:
 ;
; 
Способ 2:
Поток вызовов как последовательность случайных величин.
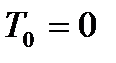 - начальный момент потока.
- начальный момент потока.
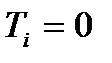 - момент поступления
- момент поступления 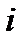 -го вызова
-го вызова 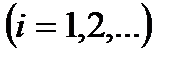
Свойства 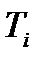 :
:
1. 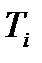 - непрерывная случайная величина;
- непрерывная случайная величина; 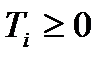 ;
;
2. 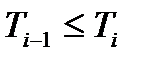 . Возможно групповое поступление вызовов.
. Возможно групповое поступление вызовов.
Пусть 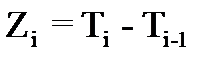 , где i>1, тогда
, где i>1, тогда 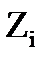 - длина промежутка времени между моментами поступления i-1 и i вызова.
- длина промежутка времени между моментами поступления i-1 и i вызова. 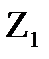 – от начального момента потока до поступления первого вызова.
– от начального момента потока до поступления первого вызова.
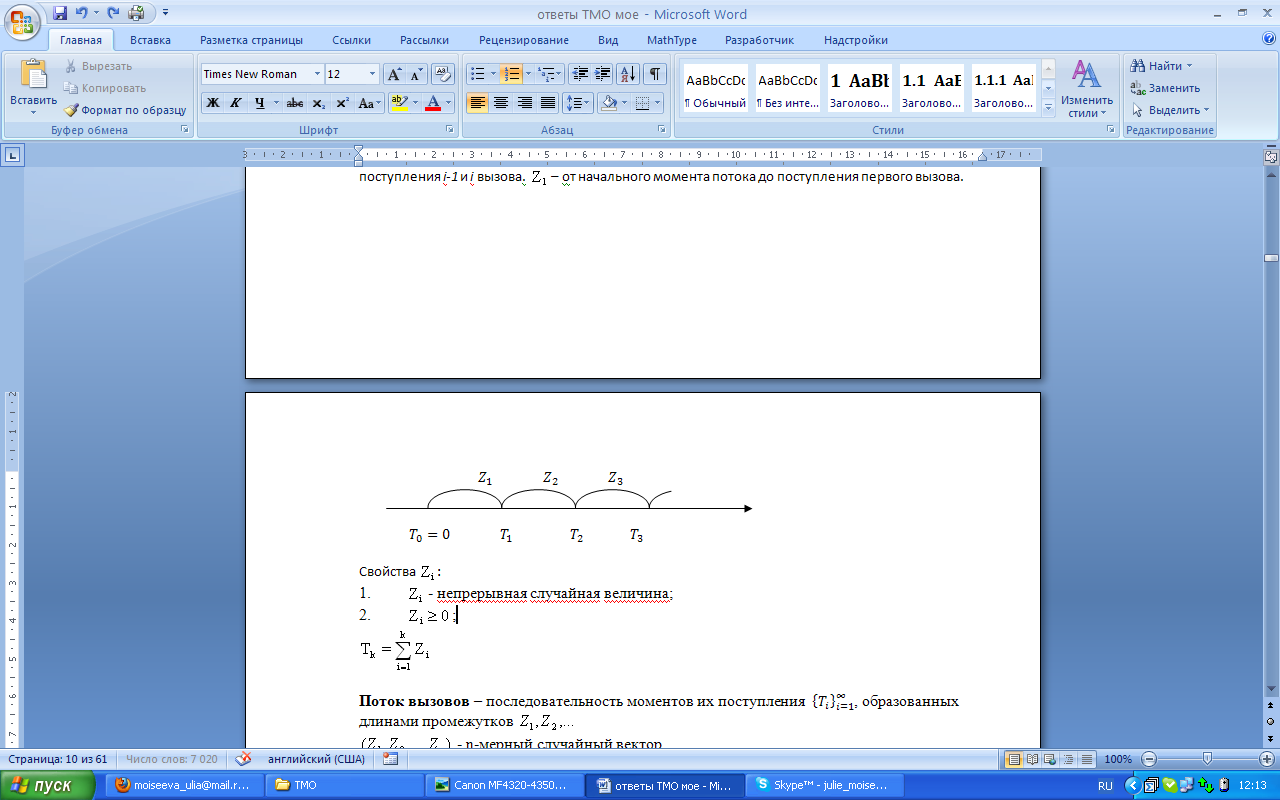 Свойства
Свойства 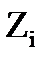 :
:
1. 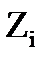 - непрерывная случайная величина;
- непрерывная случайная величина;
2. 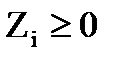 ;
;
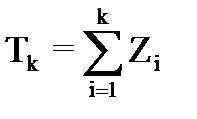
Поток вызовов – последовательность моментов поступления вызовов, образованных длинами промежутков 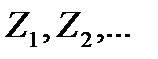
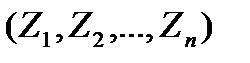 - n-мерный случайный вектор.
- n-мерный случайный вектор.
Поток задан, если известна функция распределения такого вектора:
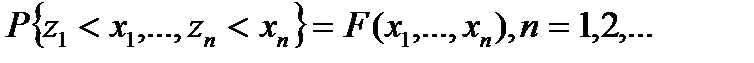 , где все Хксы положительные.
, где все Хксы положительные.
Оба способа задания потока равносильны.
Простейший поток вызовов
Поток вызовов – с.п. 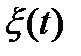
Первое определение простейшего потока:
Поток вызовов называется простейшим, если выполняются 3 условия:
1. 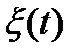 - марковский;
- марковский;
2. Вероятность поступления ровно k вызовов в промежутке времени длиной t не зависит от начального момента этого промежутка (условие стационарности);
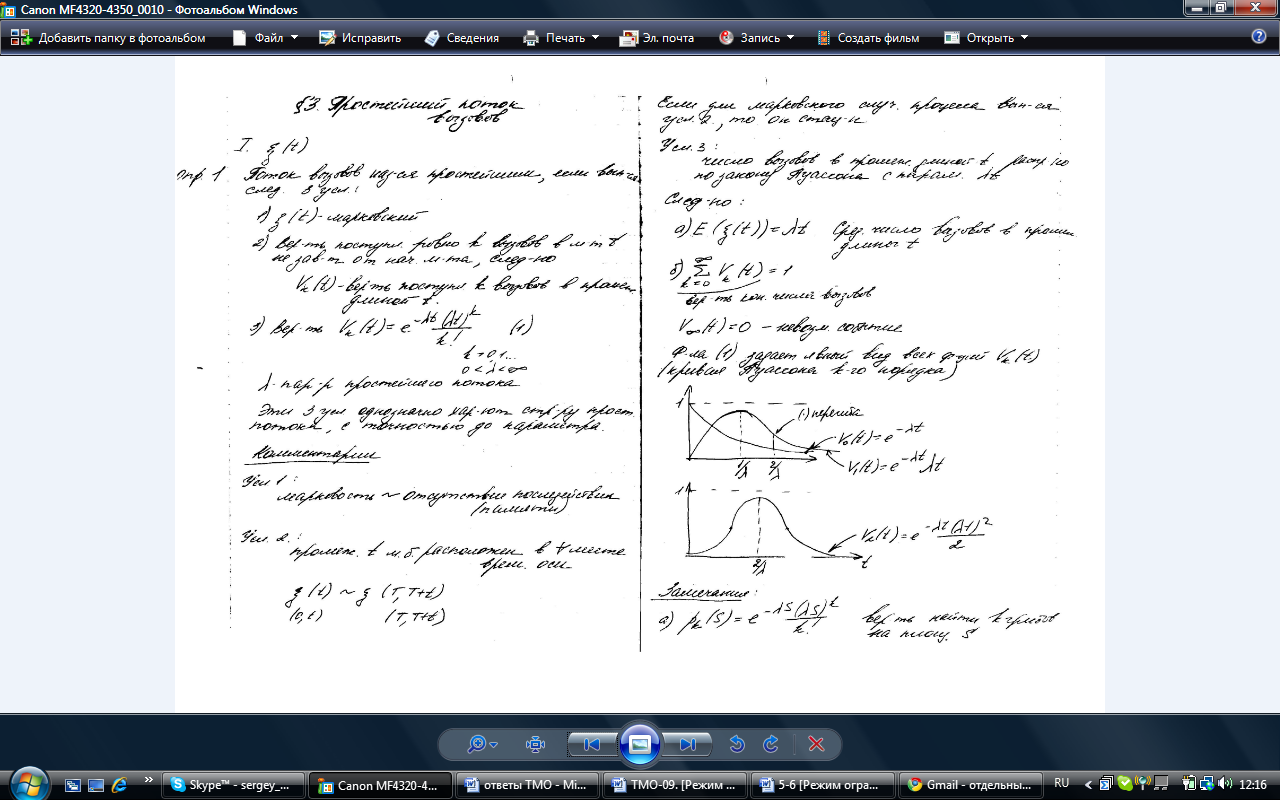
3. 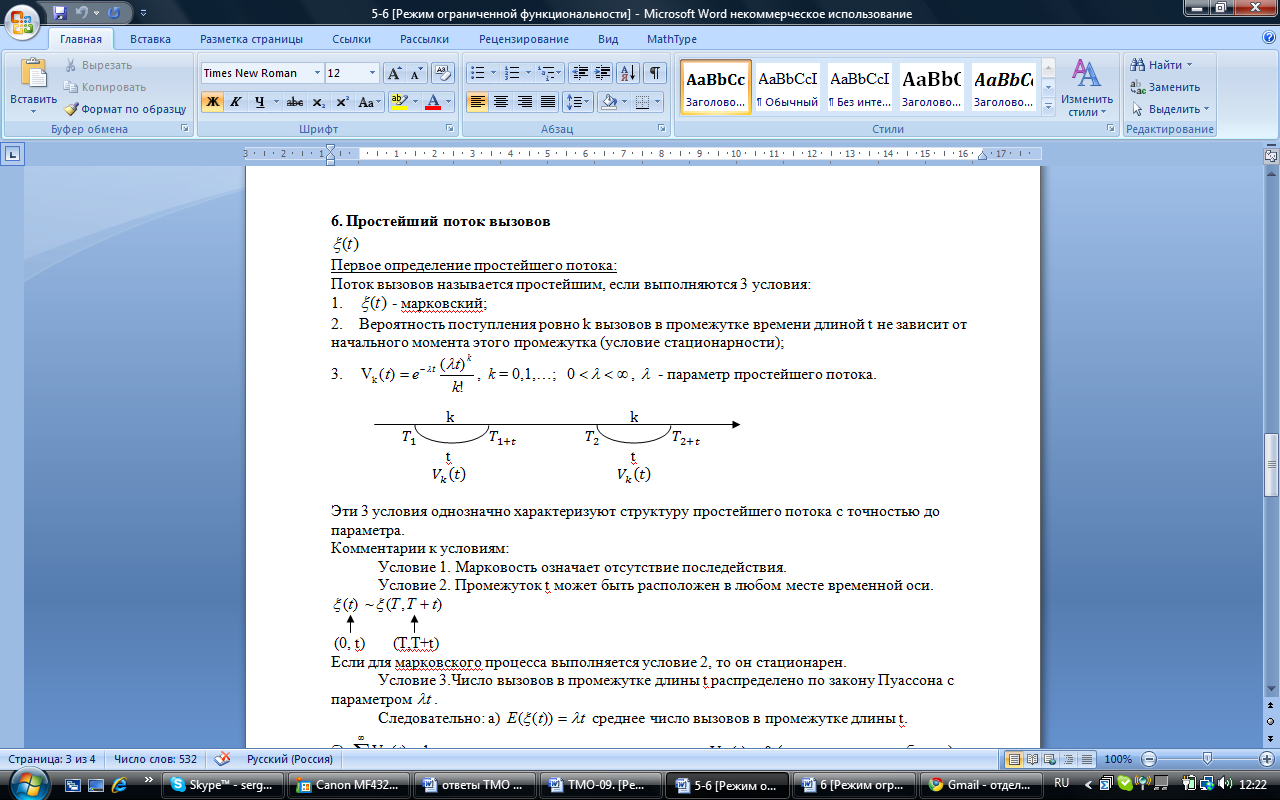
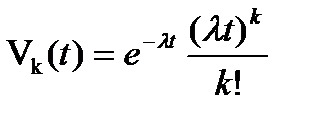 , k = 0,1,…;
, k = 0,1,…; 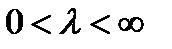 ,
, 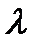 - параметр простейшего потока.
- параметр простейшего потока.
Эти 3 условия однозначно характеризуют структуру простейшего потока с точностью до параметра 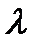 .
.
Комментарии к условиям:
Условие 1. Марковость означает отсутствие последействия.
Условие 2. Промежуток t может быть расположен в любом месте временной оси.
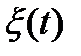 ~
~ 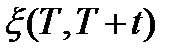 -равносильны, один и тот же закон распределения.
-равносильны, один и тот же закон распределения.
Если для марковского процесса выполняется условие 2, то он стационарен.
Условие 3.Число вызовов в промежутке длины t распределено по закону Пуассона с параметром 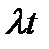 .
.
Следовательно: а) 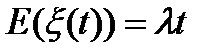 среднее число вызовов в промежутке длины t.Коэф.пропор
среднее число вызовов в промежутке длины t.Коэф.пропор 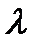
б) 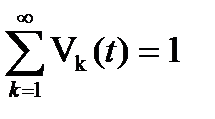 вероятность конечного числа вызовов;
вероятность конечного числа вызовов; 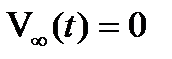 (невозможность события)
(невозможность события)
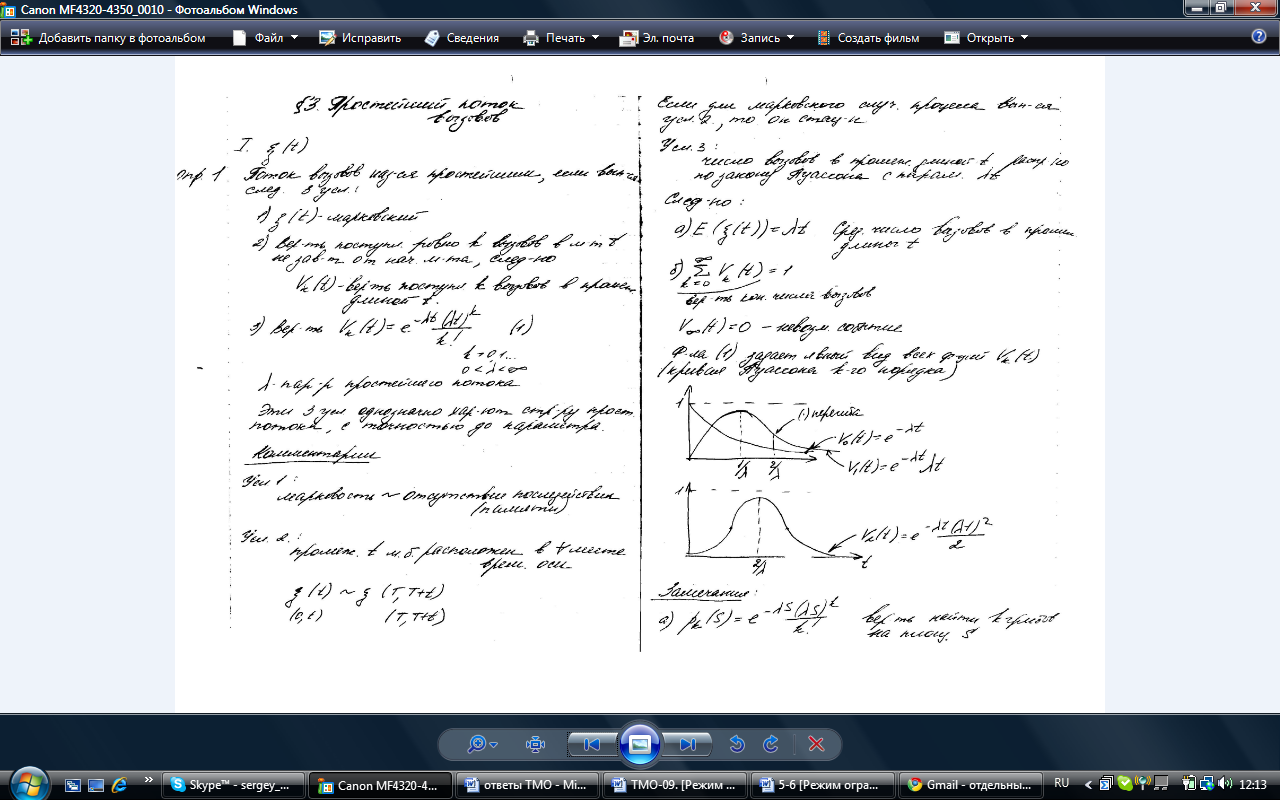
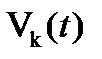 – Кривая Пуассона
– Кривая Пуассона 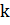 -го порядка.
-го порядка.
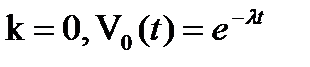
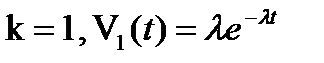
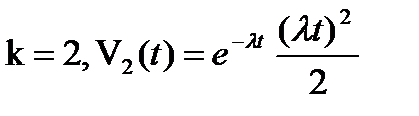
Два простейших потока могут
отличаться
друг от друга только значением
параметра.
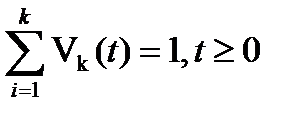
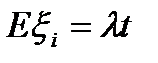
Интенсивностью 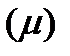 стационарного потока называется среднее число вызовов, поступающих за промежуток времени единичной длины
стационарного потока называется среднее число вызовов, поступающих за промежуток времени единичной длины 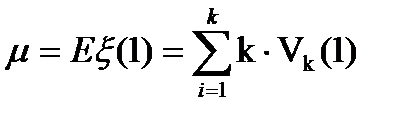 .
.
Применение: Среднее число вызовов в промежутке пропорционально длине этого промежутка, причем 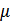 является коэффициентом пропорциональности.
является коэффициентом пропорциональности.
Доказательство: Пусть 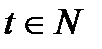 , разобьем на промежутки единичной длины: рисуем.
, разобьем на промежутки единичной длины: рисуем.
1. 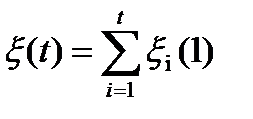
2. 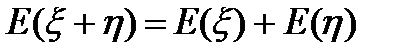
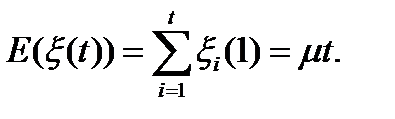 ч. т. д.
ч. т. д.
Свойства простейшего потока:
A) 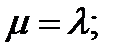
Доказательство 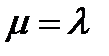 (2 варианнта):
(2 варианнта):
1. 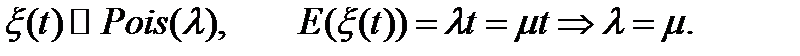
B) Средняя длина промежутка между последовательными вызовами равна 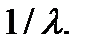
( 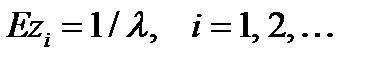 )
)
Расчет 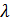 или
или 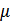 для простейшего потока:
для простейшего потока:
1. Наблюдаем за случайной величиной 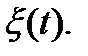
2. Регистрируем реальные значения этой величины: 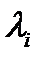 ―результат iого наблюдения (в iый промежуток ед. длины)
―результат iого наблюдения (в iый промежуток ед. длины)
3. Среднее арифметическое этих наблюдений: 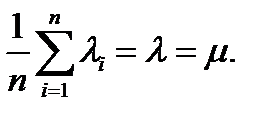
Марковость в задаче Эрланга
Если входящий поток в данную СО – простейший, время обслуживания распределено по показательному закону, то случайный процесс 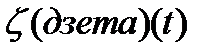 (сост. СО на t) является Марковским.
(сост. СО на t) является Марковским.
Доказательство:
Рассмотрим T- любой момент времени, 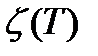 - сост. СО на T,
- сост. СО на T, 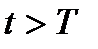 .
.
Рассмотрим будущее значение. t>T, 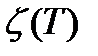 -состояние
-состояние
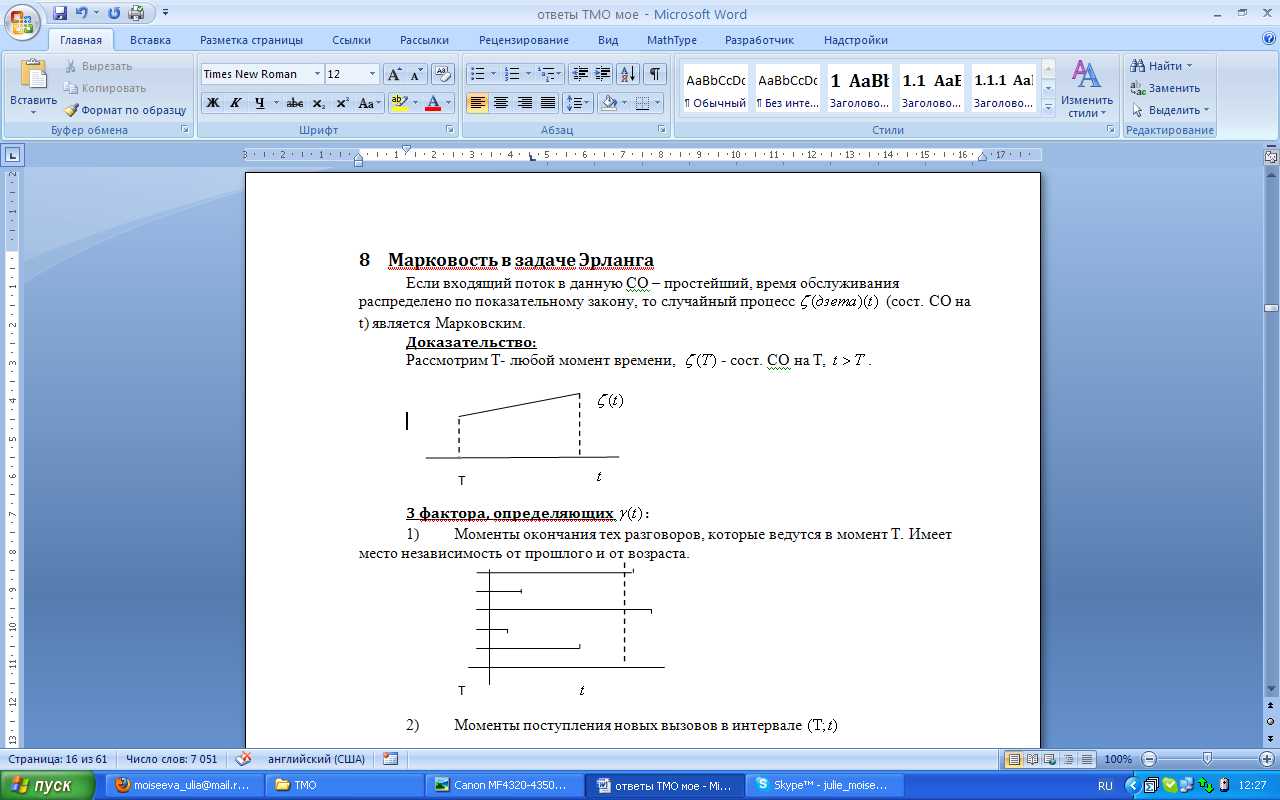
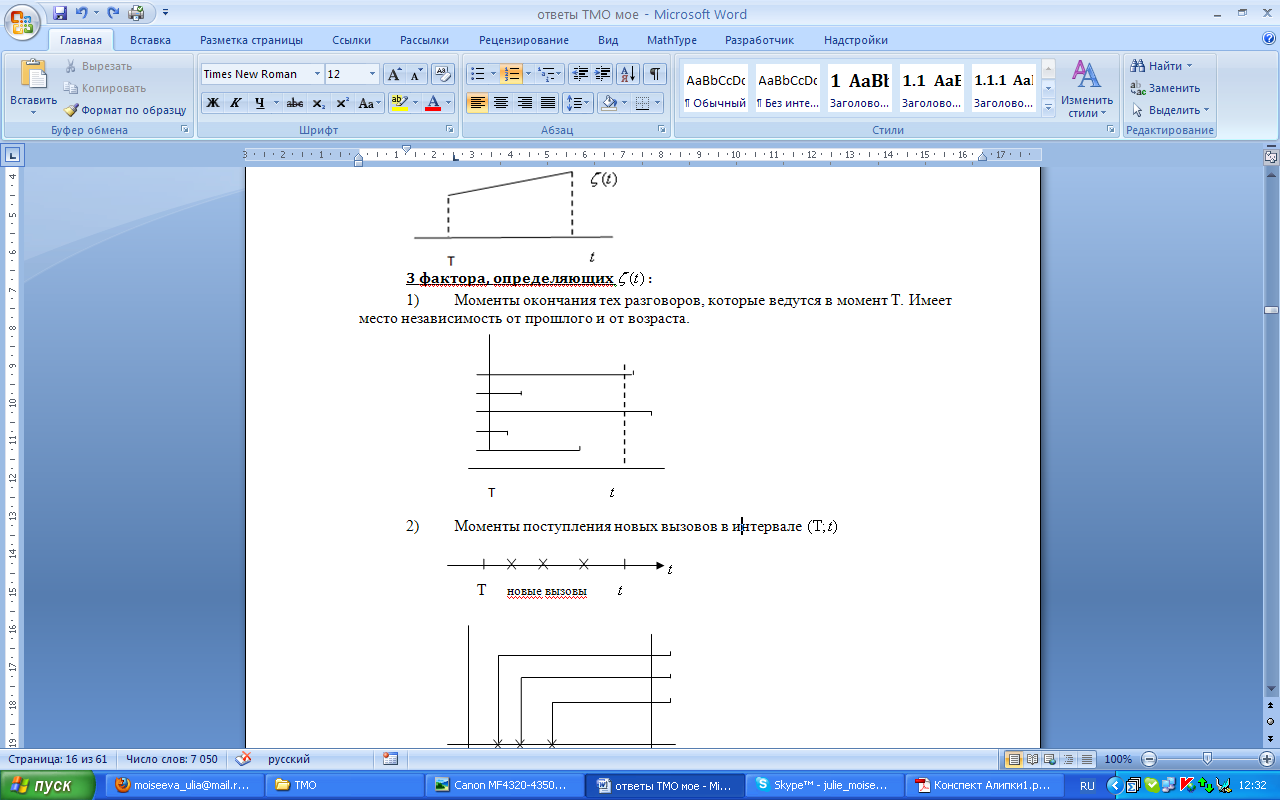
3 фактора, определяющих 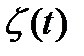 :
:
1) Моменты окончания тех разговоров, которые ведутся в момент T. Могут закончиться, а могут продолжаться.
2) Моменты поступления новых вызовов в интервале 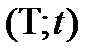
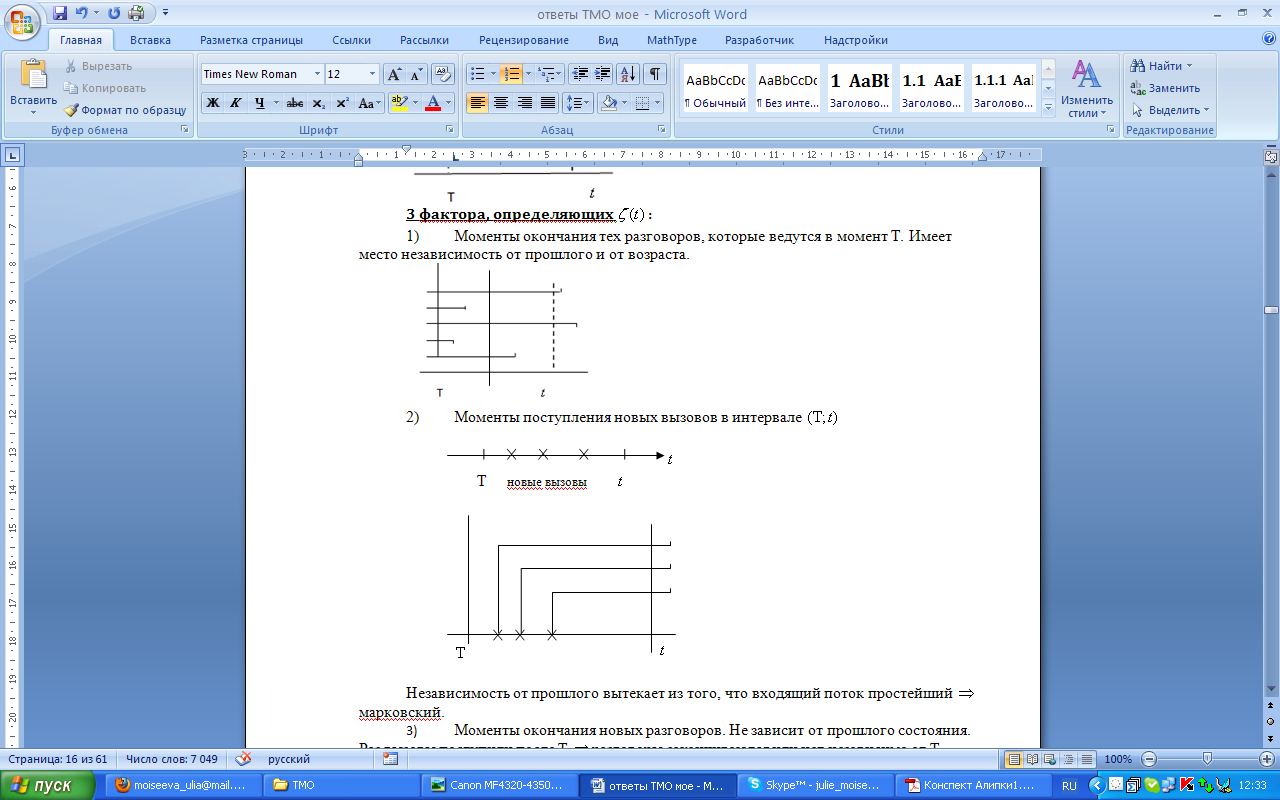
Независимость от прошлого вытекает из того, что входящий поток простейший 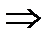 марковский.
марковский.
3) Моменты окончания новых разговоров. Не зависит от прошлого состояния. Раз вызовы поступили после T 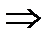 разговоры заканчиваются или нет независимо от T.
разговоры заканчиваются или нет независимо от T.
Для каждого фактора:
Для первого: из показательного закона, при котором возрастает разговор не влияет на окончание.
Для второго: это вытекает из предпосылки о простейшем потоке (явл.марковским
Для третьего: это самоопределение 3его фактора: они поступили в момент времени Т и не важно что было до!
Упорядоченный пучок линий
Пример: упаковочный цех: конвейер с упаковочными автоматами. Вызов – готовое изделие, линии – упаковочные автоматы, обслуживание – упаковка.
Допущения:
-Входящий поток – простейший с параметром 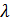 .
.
-Время обслуживания показательно распределено с параметром β.
Рассмотрим частичный пучок длины k (из первых k линий).
i-ая линия - 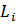
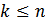 (пучок конечный)или
(пучок конечный)или 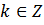 (пучок бесконечен)
(пучок бесконечен)
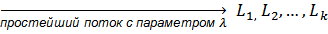
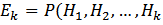 ) – вероятность отказа на пучке длины k
) – вероятность отказа на пучке длины k 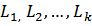 .
.
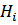 - событие, состоящее в том, что на i-ой линии не осуществилось обслуживание.
- событие, состоящее в том, что на i-ой линии не осуществилось обслуживание.
-Вычисление 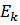 – вероятность застать все линии занятыми.
– вероятность застать все линии занятыми.
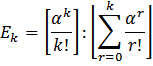
-Интепретация 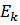
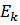 - средняя доля времени, в течение которого заняты все k линий.
- средняя доля времени, в течение которого заняты все k линий.
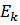 - средняя доля вызовов, получающих отказ.
- средняя доля вызовов, получающих отказ.
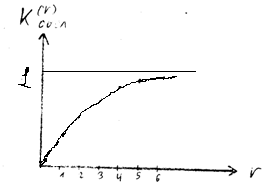
-Свойство 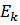 (k=1,2…). Монотонно убывает.
(k=1,2…). Монотонно убывает.
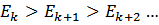
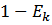 - вероятность того, что вызов будет обслужен на какой-либо из первых k линий. (возрастает).
- вероятность того, что вызов будет обслужен на какой-либо из первых k линий. (возрастает).
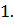 Найдем закон распределения номера линии, на которой осуществляется обслуживание вызова. Обслуживание на k-ой линии: ξ: 1, 2, …, k, …
Найдем закон распределения номера линии, на которой осуществляется обслуживание вызова. Обслуживание на k-ой линии: ξ: 1, 2, …, k, …
Найти 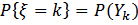 . (вероятность успеха в k-ом испытании).
. (вероятность успеха в k-ом испытании).
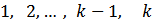
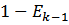
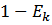
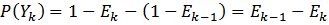 >0 (по свойству 1)
>0 (по свойству 1)
Пусть 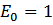
ξ = 1 2 … k
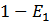

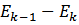
2. С ростом номера линии интенсивность потока падает.
Пусть 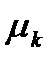 - интенсивность стационарного потока, пущенного на k-ую линию.
- интенсивность стационарного потока, пущенного на k-ую линию.
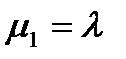 - интенсивность входящего потока.
- интенсивность входящего потока.
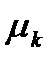 для
для 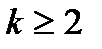
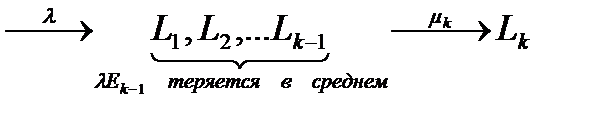
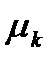 - среднее число вызовов в единицу времени.
- среднее число вызовов в единицу времени. 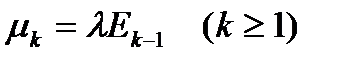
| Вероятности исходов | интенсивности | |
| Отказ на частичном пучке | 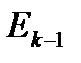 | 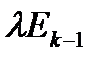 |
| обслуживание | 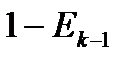 | 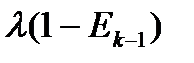 |
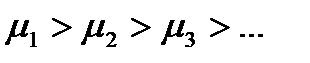
3. Поток все полнее обслуживается с повышением номера линии (полнота обслуживания измеряется коэффициентом обслуживания 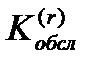 ,
, 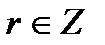 ).
).
а) 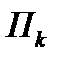 - вероятность отказа на линии r при условии того, что вызов поступил на эту линию.
- вероятность отказа на линии r при условии того, что вызов поступил на эту линию.
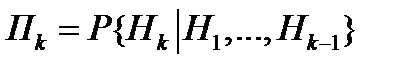
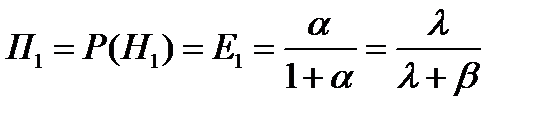
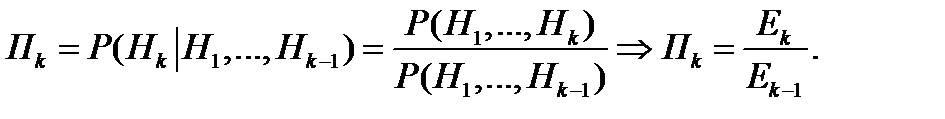
б) 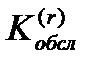 - коэффициент обслуживания – это среднее число обслуженных вызовов за единицу времени.
- коэффициент обслуживания – это среднее число обслуженных вызовов за единицу времени.
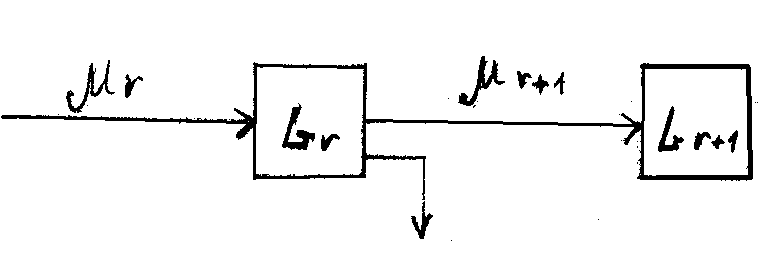
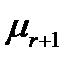 - отказы,
- отказы, 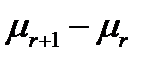 - обслуживаются.
- обслуживаются.
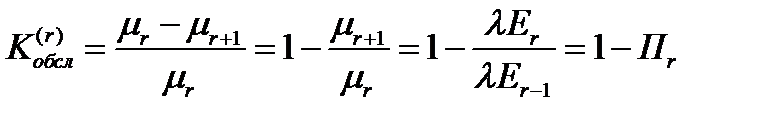
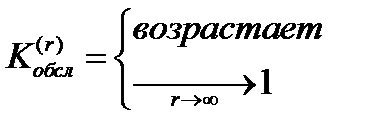
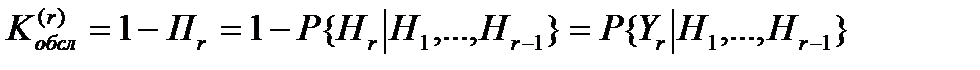 - вероятность того, что вызов будет обслужен на r-ой линии при условии того, что вызов поступил на r-ую линию.
- вероятность того, что вызов будет обслужен на r-ой линии при условии того, что вызов поступил на r-ую линию.
16.Упорядоченный пучок групп линий
Организация обслуживания.
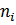 – число линий в группе с номером i.
– число линий в группе с номером i.
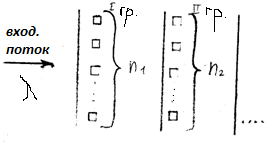
Входящий поток – простейший с параметром 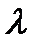 . Время обслуживания распределено показательно с параметром
. Время обслуживания распределено показательно с параметром 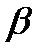 . Поступающий вызов сначала направляется в группу I если все линии заняты переходит в группу II, до тех пор пока не попадет в группу в которой есть свободные места. I, II, …, k – част. пучок длины k.(где I, II – группы)
. Поступающий вызов сначала направляется в группу I если все линии заняты переходит в группу II, до тех пор пока не попадет в группу в которой есть свободные места. I, II, …, k – част. пучок длины k.(где I, II – группы)
Пусть 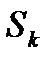 - суммарное число линий в первых k группах.
- суммарное число линий в первых k группах. 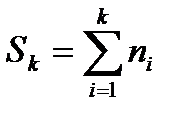
Вероятность отказа на част. пучке длины k:
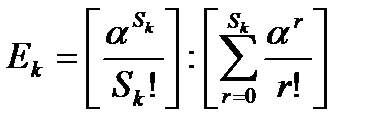 , где k – количество групп.
, где k – количество групп.
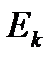 - вероятность пройти без обслуживания первых k групп.
- вероятность пройти без обслуживания первых k групп. 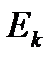 – монотонно убыв. числовая посл.
– монотонно убыв. числовая посл.
Постановка экстремальной задачи

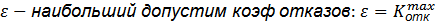 .
.
Пример упорядоченных пучков групп линий.
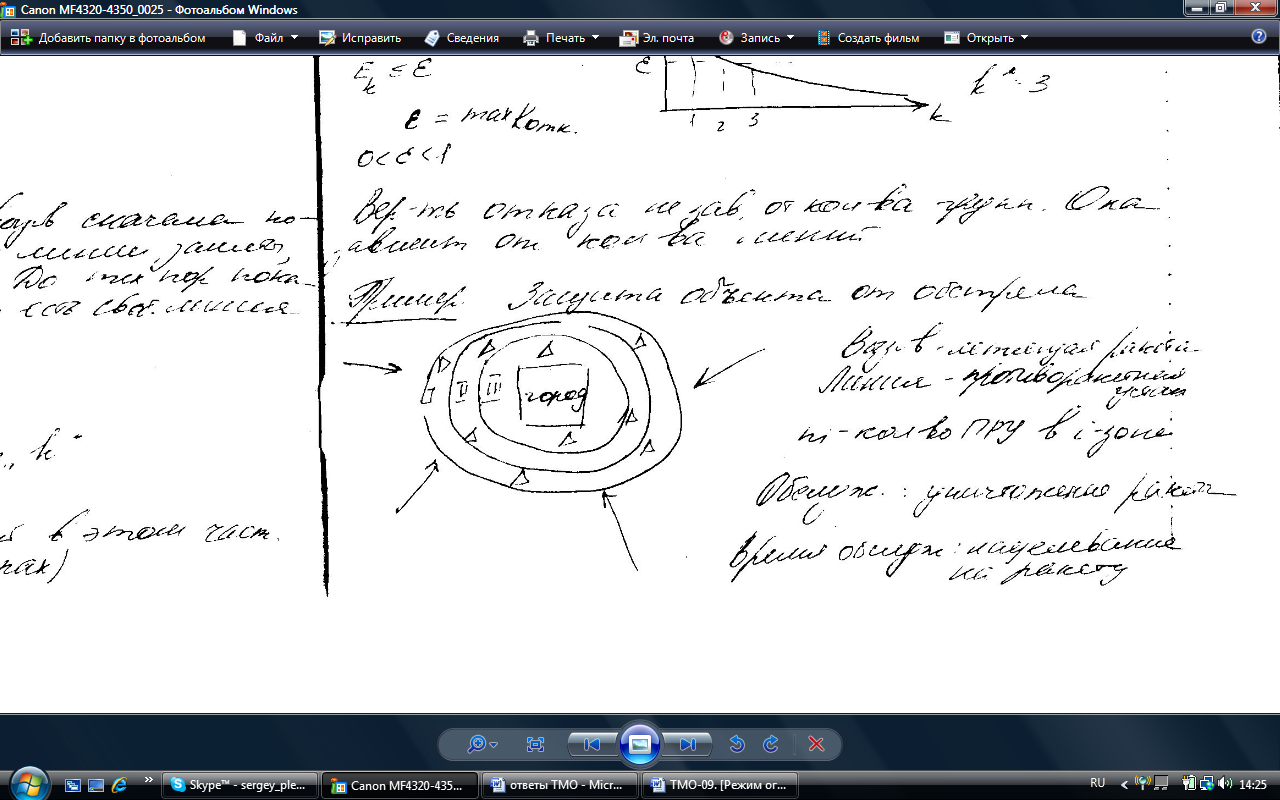 1).Защита объектов. Вызов – летящая ракета. Линия – ПРУ, Простейший поток ракет. Пусть
1).Защита объектов. Вызов – летящая ракета. Линия – ПРУ, Простейший поток ракет. Пусть 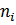 – количество ПРУ в i-ой зоне. Обслуживание – уничтожение ракеты, время обслуживания – время нацеливания на ракету.
– количество ПРУ в i-ой зоне. Обслуживание – уничтожение ракеты, время обслуживания – время нацеливания на ракету.
Ek – ракета не будет сбита в первых k зонах.
E1 =0,2; E2 =0,015 ; E3 =0,003: 200 из 1000 ракет преод. зону I, 15 – зону II, 3 – зону III.
Замечания:
А) m=0 - СОТ: 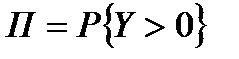 =0 ~
=0 ~ 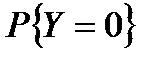 =1
=1
Б) m= 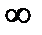 П=
П= 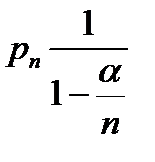 для СОЖ.
для СОЖ.
- Вероятность полной загрузки. (Вероятность того, что все линии заняты).
Пусть (полная загрузкаà) π=П+ 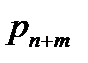 =
= 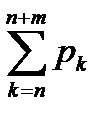 =(геометрическая прогрессия)=
=(геометрическая прогрессия)=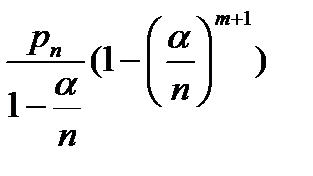
Смежный показатель – вероятность того, что есть свободная линия (вероятность немедленного обслуживания).
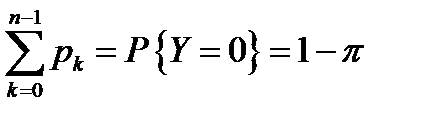
- Среднее время ожидания обслуживания.
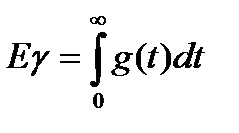 =
= 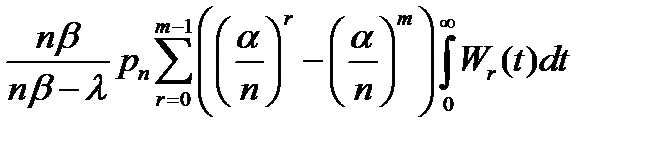 = (
= ( 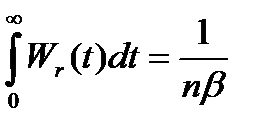 ) в соответствии с площадью под кривой Пуассона) =
) в соответствии с площадью под кривой Пуассона) = 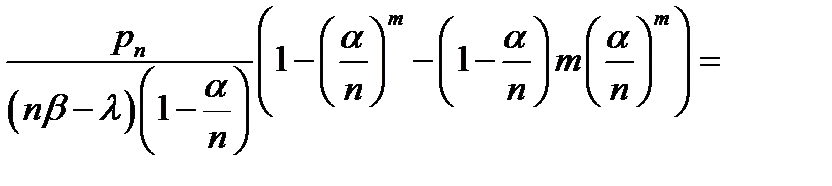
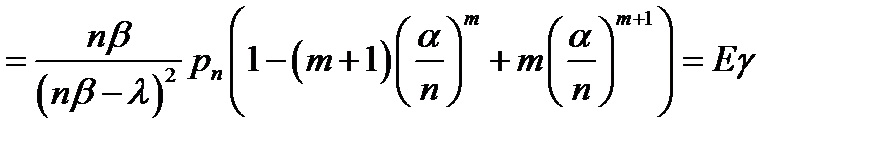
6. Среднее время пребывания вызова в СО
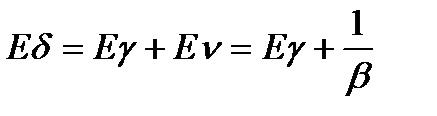
7. Средняя длина очереди:
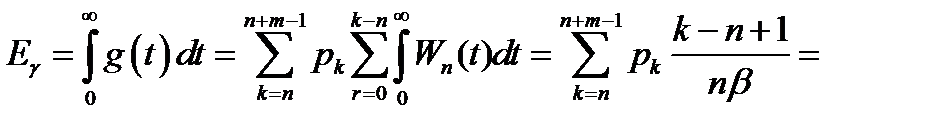
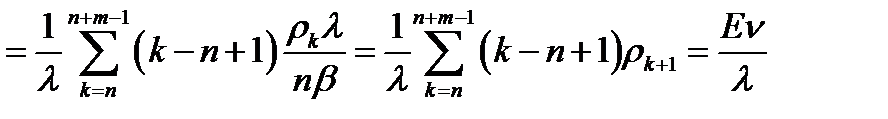
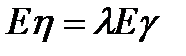
8. Среднее число вызовов в СО
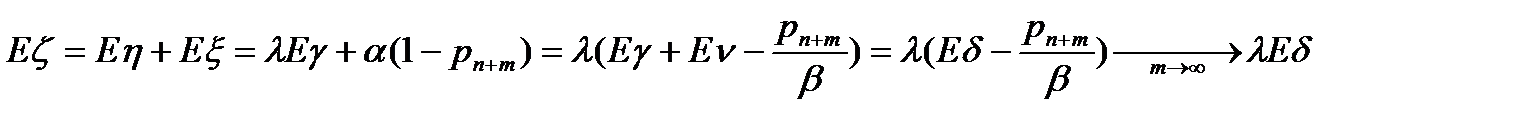
25.Оптимальное число линий в СОЧ (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
СО – магазин
Входящий поток – поток покупателей
Допущения и исходные данные:
1. Поток покупателей – простейший с параметром 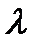 :
:
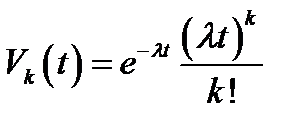 ;
; 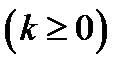 ;
; 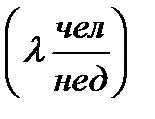
2. В одни руки отпускается только одна единица товара (спрос –пуассоновский) 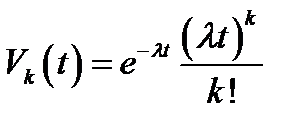
3. Как только происходит продажа товара, сразу же происходит заказ на ее замену другой единицей. Следовательно, число, равное сумме размера запаса товара и количества поданных заявок, является константой на любой момент времени
4. 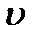 - время выполнения заказов на пополнения запаса. Распределено по показательному закону -
- время выполнения заказов на пополнения запаса. Распределено по показательному закону - 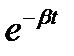
5. При отсутствии товара в магазине он задалживается, но не более чем для m покупателей
6. Пусть 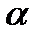 - доход от продажи единицы товара за вычетом издержек выполнения заказа на его доставку
- доход от продажи единицы товара за вычетом издержек выполнения заказа на его доставку
7. 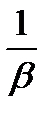 - среднее время выполнения заказов
- среднее время выполнения заказов
Пусть 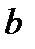 - издержки хранения единицы товара за единицу времени. Пусть
- издержки хранения единицы товара за единицу времени. Пусть 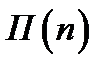 - средняя прибыль магазина за
- средняя прибыль магазина за 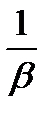 .
. 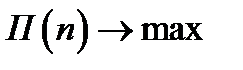 .
. 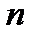 - либо максимальный размер запаса товара в магазине, либо максимальное число поданных заявок.
- либо максимальный размер запаса товара в магазине, либо максимальное число поданных заявок.
Для решения можно воспользоваться моделью СОЧ
Линия – ячейка. 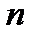 - количество линий
- количество линий
Линия занята/свободна – ячейка пуста/заполнена. Обслуживание – выполнение заказа на заполнение пустой ячейки. Время обслуживания распределено показательно 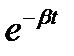
Состояние СО - 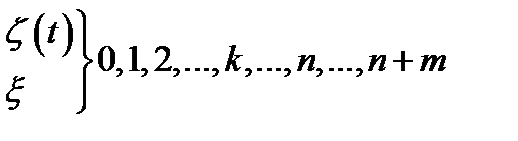 - количество поданных заказов. Если
- количество поданных заказов. Если 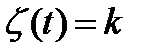 , то:
, то:
a. при 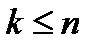 - подано “
- подано “ 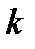 ” заявок. Следовательно, размер запаса товара равен
” заявок. Следовательно, размер запаса товара равен 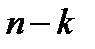
b. при 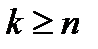 - подано “
- подано “ 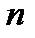 ” заявок и имеется очередь из
” заявок и имеется очередь из 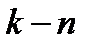 покупателей
покупателей
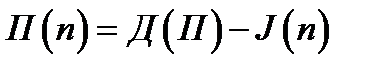 , где
, где 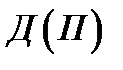 - доходы;
- доходы; 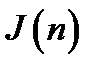 - издержки.
- издержки.
Доходы приносят реализованные единицы товара. Среднее число реализованных единиц товара за 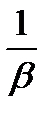 -
- 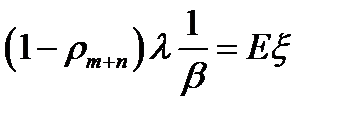 .
.
Издержки 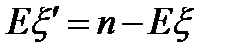 . Тогда
. Тогда 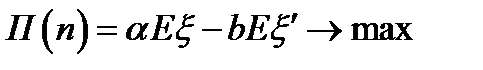
Модель замкнутой СО
I. Исходные данные
] n – количество станков в группе станков. Станки выполняют одинаковые операции. m – количество обслуживаемых объектов. ] n<m<∞ (n≥m – неинтересный случай, так как часть станков постоянно простаивает).
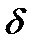 - время исправной работы объекта.
- время исправной работы объекта.
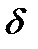 - непрерывная случайная величина, распределенная по показательному закону с параметром
- непрерывная случайная величина, распределенная по показательному закону с параметром 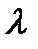 .
.
