Частотные критерии устойчивости СУ

Эти критерии позволяют судить об устойчивости СУ по виду ЧХ.

Здесь рассмотрим наиболее часто используемый частотный критерий Найквиста. Основная специфика этого критерия следующая. Критерий Найквиста позволяет анализировать устойчивость замкнутой системы по амплитудно-фазочастотной (АФЧХ) разомкнутой системы.

1.2.2.1. Формулировка критерия Найквиста для АФЧХ

Критерий устойчивости Найквиста изначально сформулирован для АФЧХ разомкнутой САУ W_раз(jw). На комплексной плоскости фиксируется так называемая критическая точка с координатами (-1, j0) – см. рис. 5. При изменении частоты w от 0 до µ, прохождение годографа W_раз(jw) через отрицательную часть мнимой оси означает, что точке пересечения годографа с осью соответствует фазовый сдвиг -p. Частота на АФЧХ в точке пересечения обозначается “w_π”.

Критерий Найквиста определяет устойчивость замкнутой САУ по положению точки пересечения W_раз(jw_π) и критической точки (-1, j0) разомкнутой САУ.

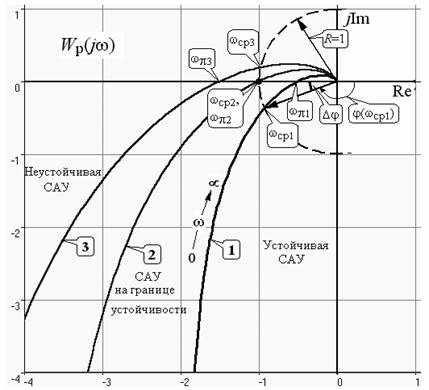
Рис. 5

Если точка АФЧХ WР(jwp) находится слева от точки (-1, j₀), то говорят, что АФЧХ “охватила” критическую точку. При этом имеем модуль АФЧХ R_Р(wp) > 1.

Если точка АФЧХ W_Р(jwp) находится справа от точки (-1, j₀), то говорят, что АФЧХ “не охватила” критическую точку. При этом имеем модуль АФХ R_Р(wp) < 1.

Теперь можем сформулировать простые правила критерия Найквиста.

· Если при изменении частоты w от 0 до µ АФЧХ W_Р(jw) не охватывает критическую точку, то замкнутая система будет устойчивой.

· Если при изменении частоты w от 0 до µ АФЧХ W_Р(jw) охватывает

критическую точку, то замкнутая САУ будет неустойчивой, т.е. возбудится на частоте, на которой выполняется баланс амплитуд и баланс фаз.

· Если при изменении частоты w от 0 до µ АФЧХ W_Р(jw) проходит через критическую точку, при этом замкнутая САУ будет находится на границе устойчивости.

На рис. 5 изображена комплексная плоскость, на которой построена полуокружность единичного радиуса и отмечена точка (-1, j₀).

Построим АФЧХ для той же САУ, устойчивость которой исследовалась алгебраическим критерием.

Кривая “1” соответствует значению коэффициента усиления K = 1< K_кр. Действительно, в этом случае АФЧХ W_Р(jw) не охватывает критическую точку и при замыкании обратной связи САУ будет устойчивой (рис. 4, а).

Кривая “2” построена при значении коэффициента усиления K = 2 = K_кр. В этом случае АФЧХ W_Р(jw) прошла через критическую точку и замкнутая система находится на колебательной границе устойчивости – см. рис. 4,б.

Кривая “3” соответствует значению коэффициента усиления K = 3 > K_кр. В этом случае АФЧХ W_Р(jw) охватила критическую точку, то есть замкнутая система неустойчива – см. рис. 4,в.

Точка пересечения АФЧХ W_Р(jw) с окружностью единичного радиуса (то есть единичного модуля АФЧХ) соответствует частоте w_ср. Поэтому можно дать другую формулировку частотному критерию (см. рис. 5):

· при w_ср< wp система устойчива;

· при w_ср> wp система неустойчива;

· при w_ср= wp система находится на границе устойчивости.

Для устойчивых САУ с использованием критерия Найквиста вводятся количественные оценки “запасов” устойчивости. Наиболее распространенная оценка – запас по фазе Dj. Под ним понимают значение угла, на который следует “довернуть” вектор R(w_ср) до значения -p (см. рис. 5). Для “хороших” САУ с переходным процессом, имеющим перерегулирование s < 15%, должно выполняться Dj > (55¸60о).

1.2.2.2. Применение критерия Найквиста для ЛАЧХ

Построим АЧХ для рассмотренного выше примера САУ в логарифмическом масштабе – ЛАЧХ (рис. 6).

В данном случае удобнее пользоваться второй формулировкой критерия Найквиста.

Для кривой “1” имеет место w_ср< wp и система устойчива. При этом на рисунке показан запас по фазе Dj. Также видно, что кривой “3” соответствует w_ср> wpи система неустойчива. При w_ср= wpимеем кривую “2” и систему на границе устойчивости.

Можно дать формулировку критерия для ЛАЧХ:

· если L_Р(wp) < 0, то система устойчива;

· если L_Р(wp) > 0, то система неустойчива;

· если L_Р(wp) = 0, то система на границе устойчивости.

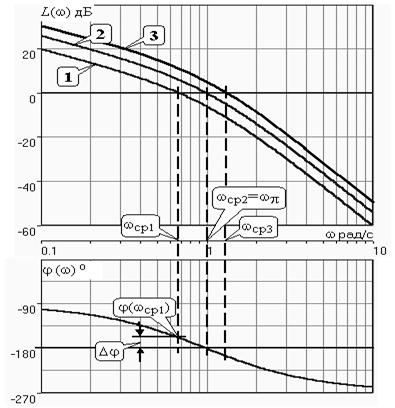
Рис.6

Критерий устойчивости Найквиста при использовании ЛЧХ позволяет легко определить критический коэффициент усиления для САУ высокого порядка. Действительно, при вариациях усиления в контуре, ФЧХ остается неизменной, а ЛАЧХ смещается параллельно самой себе вверх (при увеличении усиления) или вниз (при уменьшении усиления). Необходимо расположить ЛАЧХ таким образом, чтобы выполнилось w_ср= wpили, что то же самое, L_Р(wp) = 0. После фиксации ЛАЧХ по ее низкочастотному участку определяется коэффициент усиления в контуре.