Кинематическое исследование механизма графоаналитическим методом

Геометрический синтез зубчатого механизма

Одним из основных достоинств зубчатого зацепления механизмов является его компактность при передаче большой мощности. Для уменьшения геометрических размеров зубчатых колес и механизма в целом используют зубчатые колеса с минимальным числом зубьев. Однако при изготовлении зубчатых колес с числом зубьев меньше 17 происходит подрез эвольвентной части зуба в районе ножки. Во избежание подрезания профиля зуба режущий инструмент при изготовлении зубчатых колес отодвигается от центра заготовки (положительное смещение). Изготовленные таким образом зубчатые колеса со смещением имеют большую прочность и устойчивость к износу, но меньший коэффициент перекрытия ε_α, показывающий сколько пар зубьев одновременно находится в зацеплении.

Величина смещения инструмента «а» определяется из соотношения:

a = xm,

где х- коэффициент смещения,

m- модуль зубчатого колеса.

Правильно выбранный коэффициент смещения обеспечивает получение необходимых свойств и геометрических параметров зубчатой передачи. В связи с этим при выборе коэффициентов смещения необходимо пользоваться рекомендациями по проектированию зубчатых передач с заданными свойствами.

Так, например, для силовых передач общего назначения при выборе коэффициентов смещения можно пользоваться рекомендациями, приведенными в таблице 2.

Таблица 2 Рекомендуемые значения коэффициентов смещения

Числа зубьев z1 и z2	x1	x2
z1,2≥30
z1=14-20 z2≥50	0,3	-0,3
z1=10÷30 z2≤30	0,5	0,5
z1= 10…30 z2≥ 32	0,5
z1=5…9 z2≤ 30	Х1=0,03(30-z1)	Х2=0,03(30-z2)

В специальной литературе имеются рекомендации по выбору коэффициентов смещения при проектировании зубчатых передач с различными свойствами [2].

Выбор коэффициентов смещения можно осуществить также по так называемым блокирующим контурам.

После выбора коэффициентов смещения х₁ и х₂ при заданных числах зубьев z₁ и z₂ и модуля зацепления m определяем основные размеры зубчатых колес и качественные характеристики зацепления.

Суммарный коэффициент смещения:

Х_∑=х₁+х₂

Эвольвентная функция (инвалюта) угла зацепления α_w:

inv α_w=invα+2((x₁+x₂)/z₁+z₂)tgα,

где α - угол профиля реечного инструмента (α=20º).

Угол α_w находят по таблицам эвольвентной функции. При необходимости определения инвалюты угла пользуются следующей формулой:

invα_i= tgα_i - α_i,

где α_i - угол в радианах.

Все геометрические параметры зубчатой передачи определяются в миллиметрах.

Диаметры делительных окружностей:

d₁=mz₁

d₂=mz₂

Диаметры основных окружностей:

d_в1=d₁cosα

d_в2=d₂cosα

Делительное межосевое расстояние:

a=(m(z₁+z₂))/2

Межосевое расстояние передачи со смещением:

a_w=a(cosα)/ cosα_w

Коэффициент воспринимаемого смещения:

у=(а_W-a)/m

Коэффициент уравнительного смещения:

∆у=х_∑-у

Радиусы начальных окружностей:

r_w1=r₁(cosα)/ cosα_w

r_w2=r₂(cosα)/ cosα_w

Контрольная проверка:

a_w=r_w1+r_w2

Радиусы вершин зубьев:

r_a1=m((z₁/2)+h_a^*+x₁-∆y)

r_a2=m((z₂/2)+h_a^*+x₂-∆y)

Радиусы окружностей впадин зубьев:

r_f1=m((z₁/2)-h_a^*+x₁-с^*)

r_f2=m((z₂/2)-h_a^*+x₂-с^*)

Высота зуба:

h=r_a1-r_f1

Толщина зубьев по делительной окружности:

S₁=m((π/2)+2x₁tgα)

S₂=m((π/2)+2x₂tgα)

Угол профиля в точке на окружности вершин:

α_a1=arccos(r_в1/r_a1)

α_a2=arccos(r_в2/r_a2)

Толщина зубьев по окружности вершин:

S_a1=m(cosα/cosα_w)[(π/2)+2x₁tgα-z₁(invα_a1-invα)]

S_a2=m(cosα/cosα_w)[(π/2)+2x₂tgα-z₂(invα_a2-invα)]

Толщина зубьев по окружности вершин должна быть больше или равна 0,4m, коэффициенты высоты головки зуба h_a^* = 1, коэффициент радиального зазора с^*=0,25.

Коэффициент торцового перекрытия:

ε_α=(z₁/2π)(tgα_a1-tgα_w)+(z₂/2π)(tgα_a2-tgα_w) ≥ [ε_α]

В зависимости от точности изготовления зубчатых колес минимальная величина коэффициента перекрытия принимается от 1,05 до 1,35. Например, если ε_α= 1,2, то в зацеплении находится в среднем 1,2 пар зубьев, а фактически в течение 20% времени работы передачи в зацеплении находятся две пары зубьев, а в течение 80% - одна пара.

На основании выполненных расчетов вычерчивается зацепление 2х зубчатых колес с определением активной линии зацепления и активной части профилей зубьев.

Кинематическое исследование механизма графоаналитическим методом

2.1.1 Определение скоростей звеньев механизма с помощью плана скоростей

Обычно принимается, что кривошип вращается с постоянной угловой скоростью. Линейная скорость точки А кривошипа, как известно, определяется по формуле:

,

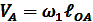где ω₁ - угловая скорость вращения кривошипа, которая определяется по формуле:

^,

class=Section2>

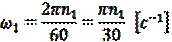где n₁ - число оборотов кривошипа в минуту (мин^-1).

Вектор скорости точки, движущейся по какой-либо траектории, всегда направлен по касательной к траектории в этой точке. В нашем случае вектор скорости точки А направлен по касательной к окружности, т.е. перпендикулярен к радиусу ОА. Из произвольной точки P_V на плоскости проводим отрезок 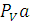произвольной длины (рекомендуется не менее 100 мм) (рис.3), который будет в масштабе 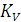(масштабный коэффициент скорости) изображать скорость точки. Величина 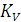будет равна:

^,

class=Section3>

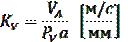т.е. масштабный коэффициент показывает: сколько единиц скорости содержится в одном миллиметре отрезка .

Далее определяем скорость точки В, принадлежащей одновременно звеньям 2 и 3. Звено 2 совершает сложное плоскопараллельное движение. В сложном движении скорость точки В определим в соответствии с векторным уравнением:

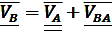,(1)

где 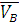- вектор скорости точки В

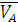- вектор скорости точки А

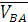- вектор скорости точки В относительно А.

В векторном уравнении (1) скорость точки А известна по величине и по направлению, скорости V_B и V_ВA известны только по направлению. Скорость точки В направлена по линии ОВ (движение ползуна-поршня 3 по направляющим), вектор скорости точки В относительно точки А будет направлен перпендикулярно шатуну АВ как радиусу окружности, описываемой точкой В в ее относительном движении вокруг точки А. В соответствии с этим из точки P_V проводим луч параллельный линии ОВ, а из точки 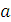отрезка 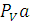луч, перпендикулярный АВ. Пересечение этих лучей в точке 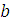является решением векторного уравнения (1) и определяет отрезок 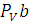, который в принятом масштабе изображает скорость точки В, а отрезок 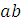изображает скорость точки В относительно точки А.

Направление векторов этих скоростей должно соответствовать уравнению (1), а их величина определяется из соотношений:

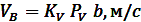
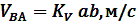
Аналогичным образом определяются скорость точки С и точки С относительно точки А.Положение точек S₂ и S₄( центров масс), звеньев на плане скоростей определяется в соответствии с условием подобия : их расположение не плане скоростей подобно расположению на схеме механизма. Так, например, если точка S₂ находится на одной трети отрезка АВ, а точка S₂ на плане скоростей будет также находиться на одной трети отрезка 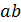. Соединив точки S₂ и S₄ с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из cоотношения:

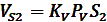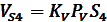, м/c

, м/c

Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении.

Как уже говорилось, отрезок плана скоростей аb (вектор) обозначает скорость точки В относительно точки А. Разделив величину скорости 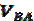на действительную длину звена АВ получим угловую скорость звена 2:

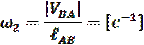
Для определения направления угловой скорости ω₂ необходимо вектор скорости 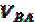приложить к точке В (см. рис 1.), посмотреть в какую сторону звено АВ будет вращаться относительно точки А и в соответствующую сторону направить ω₂. В рассматриваемом случае звено 2 вращается против часовой стрелки.

Угловая скорость звена 4 и ее направление определяются аналогичным образом:

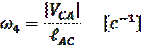
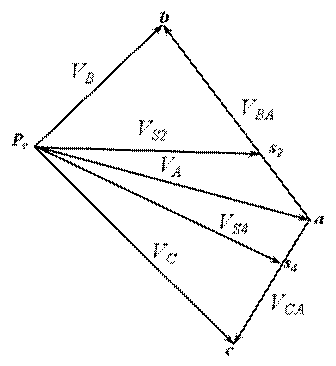
Рис.3 План скоростей

2.1.2 Определение ускорений звеньев механизма с помощью плана ускорений

Построение плана ускорений также начинаем со звена 1. В общем случае ускорение точки А, лежащей на кривошипе определяется из векторного уравнения:

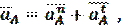
где 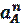- нормальное (центростремительное) ускорение точки А.

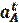- тангенциальное ускорение точки А.

Так как кривошип вращается с постоянной угловой скоростью (ω₁=const), то 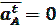.Центростремительное ускорение точки А определим по формуле:

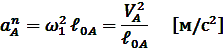
Построение плана ускорений (рис.4) начинаем с ускорения 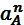, которое направлено по кривошипу к центру его вращения О. Для этого из произвольной точки P_a проводим луч P_aа произвольной длины (не менее 100 мм) по направлению действия 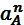. Зная величину ускорения 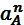и длину отрезка P_aа (мм), определяем масштабный коэффициент плана ускорений :

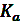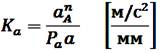
Ускорение точки В в сложном движении шатуна определим в соответствием с векторным уравнением:

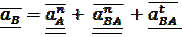⁽²⁾

В уравнении (2) имеется 3 неизвестных по величине параметра 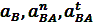, при известном их направлении. Для графического решения уравнения (2) необходимо определить величину одного из неизвестных параметров, в частности величину нормального ускорения точки В относительно точки А:

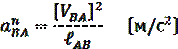
Центростремительное ускорение 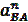направлено от точки В к точке А, как мгновенному центру вращения,по шатуну АВ. Величину отрезка, изображающего ускорение 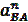на плане ускорений определим из соотношения:

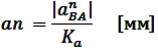
Определив величину ускорения 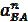и отложив на чертеже отрезок аn решаем уравнение (2) графически. Для этого из точки Р_а (полюса плана ускорений) проводим луч, параллельный линии ОВ, который соответствует направлению вектора ускорения точки В, до пересечения с направлением вектора тангенциального ускорения 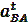, перпендикулярного шатуну АВ.

Полученная фигура (план ускорений) является графическим решением уравнения (2), поэтому направления векторов на этой фигуре должны соответствовать данному уравнению. Величину искомых ускорений определяем умножением соответствующих отрезков из плана на К_а:

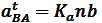
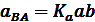
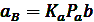
На плане ускорений, так же как на плане скоростей, определяем положение точек S₂ и S₄ в соответствии с теоремой подобия, после чего находим величину ускорений центров масс шатунов 2 и 4:

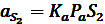
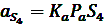
Для звеньев 4 и 5 искомые ускорения определяем аналогичным образом в соответствии с уравнениями:

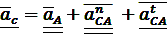
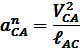
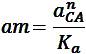
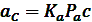
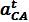
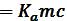
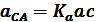
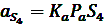
План ускорений позволяет определить величину и направление угловых ускорений шатунов. Угловое ускорение шатуна 2:

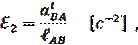
угловое ускорение шатуна 4:

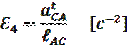
Направление этих ускорений определяется по направлению тангенциальных ускорений, приложенных в соответствующих точках по аналогии с угловыми скоростями (см. рис.1 и рис.4).

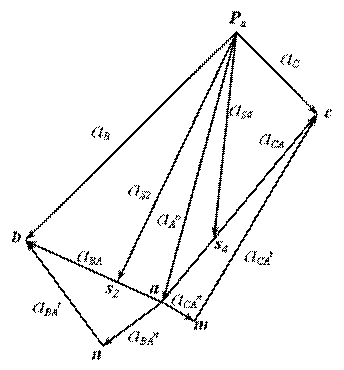
Рис.4 План ускорений

Планы скоростей и ускорений позволяют определить характер движения звеньев механизма. При одинаковом направлении скорости и ускорения звенья движутся ускоренно, при разном направлении - замедленно. В случае ω ≠ 0 и ε = 0 – равномерно; случай ω = 0 и ε ≠ 0 – указывает на то, что скорости различных точек звена равны, например, для звена 2 (V_A = V_B), т.е. звено движется поступательно.

В нашем случае: звено 1 движется равномерно (по условию), звено 2 - ускоренно, звено 3 - замедленно, звено 4 - замедленно, звено 5 -ускоренно.

Отметим, что кинематический анализ механизма для полноты картины изменения параметров целесообразно осуществлять за цикл, который в данном механизме соответствует полному обороту кривошипа.

В предположении, что кинематические параметры механизма не изменяются скачкообразно, их определяют для восьми, двенадцати и более положений кривошипа в зависимости от условий поставленной задачи.

В этом случае план механизма, планы скоростей и ускорений строятся для каждого из этих положений.