Касательная плоскость и нормаль к поверхности

Определение.Касательной плоскостью к поверхности в ее точке 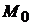(точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Определение.Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности задано в явной форме 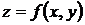, то уравнение касательной плоскости в точке 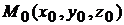имеет вид

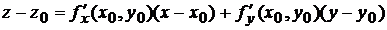, (6.1)

а уравнение нормали –

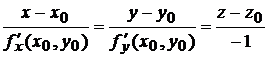. (6.2)

Если уравнение поверхности задано в неявной форме 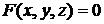, то уравнение касательной плоскости в точке 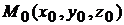имеет вид

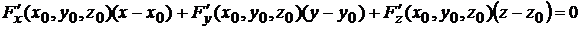. (6.3)

Уравнение нормали

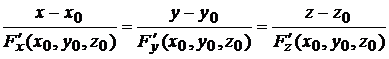. (6.4)

Указания к задаче 6.

6.1. Составить уравнение касательной плоскости и уравнения нормали к поверхности 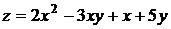в точке А(1,2,7).

Решение. Если уравнение поверхности задано в явной форме 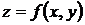, то уравнение касательной плоскости в точке 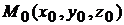имеет вид (6.1)

,

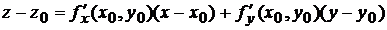а уравнение нормали (6.2) –

.

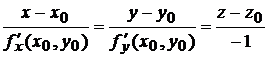Найдем значения частных производных 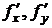в точке М:

, .

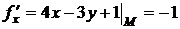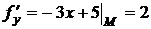Подставляя найденные значения в уравнения касательной плоскости и нормали, получим

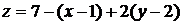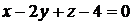или - уравнение касательной плоскости, 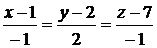- уравнение нормали.

6.2. Составить уравнение касательной плоскости и уравнения нормали к поверхности 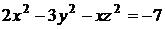в точке А(1,0,3).

Решение. Если уравнение поверхности задано в неявной форме 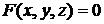, то уравнение касательной плоскости в точке 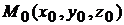имеет вид (6.3)

.

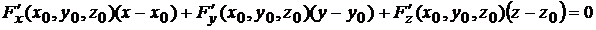Уравнение нормали (6.4)

.

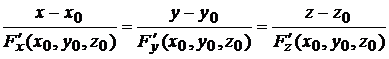Найдем значения частных производных 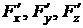в точке М:

, , .

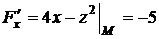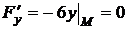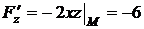Подставляя найденные значения в уравнения касательной плоскости и нормали, получим

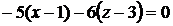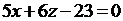или - уравнение касательной плоскости, 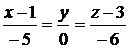- уравнение нормали.

Градиент и производная по направлению

Пусть функция 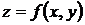определена в окрестности точки 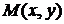и пусть 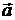- вектор, исходящий из этой точки. На векторе 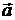возьмем точку .

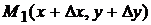Определение.Производной функции 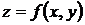по направлению 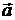в точке 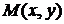называется предел (если он существует)

,

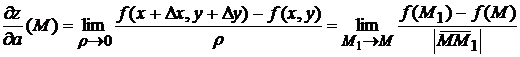где .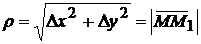

Определение.Градиентом функции 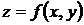в точке 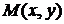называется вектор, проекциями которого являются значения частных производных функции в этой точке, т.е.

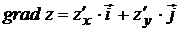. (7.1)

Замечание. Аналогично определяются производная по направлению и градиент функции 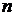переменных .

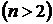Градиент и производная по направлению 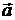связаны между собой соотношением

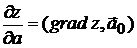, (7.2)

т.е. производная по направлению 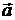равна скалярному произведению градиента на единичный вектор .

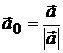Указания к задаче 7.

Даны: функция 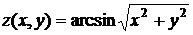,точка 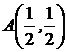и вектор .

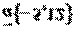Найти: 1) 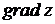в точке А;

2) производную в точке А по направлению вектора .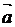

Решение.

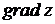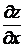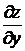Найдем в точке А , для этого вычислим и в точке А. Имеем:

,

.

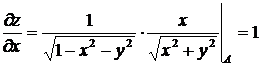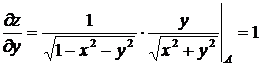Таким образом, .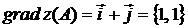

Для нахождения производной функции 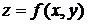в направлении вектора 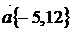воспользуемсяформулой (7.1). Для этого найдем единичный вектор 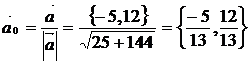, тогда

.

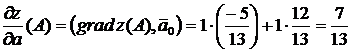8. Экстремум функции нескольких переменных

Пусть функция 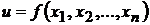определена в некоторой окрестности точки .

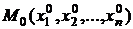Определение.Функция 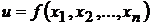имеет максимум (минимум) в точке 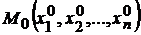, если существует такая окрестность точки 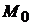, в которой для всех точек 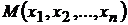( 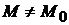) выполняется неравенство 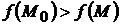(соответственно ).

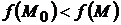Максимум или минимум функции называется ее экстремумом, а точки, в которых функция имеет экстремум, называются точками экстремума (максимума или минимума).

Необходимое условие экстремума.Если функция 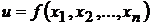имеет экстремум в точке 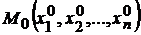, то в этой точке

.

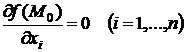Точки, в которых выполняются эти условия, называются стационарными точками функции .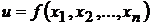

Достаточное условие экстремума.Пусть 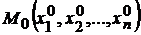- стационарная точка функции 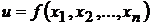, причем эта функция дважды дифференцируема в некоторой окрестности точки 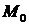и все ее вторые частные производные непрерывны в точке 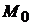. Тогда:

если второй дифференциал 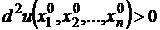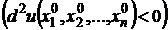при любых значениях 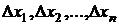, не равных одновременно нулю, то функция 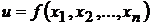имеет в точке 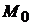минимум (максимум);

если 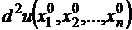принимает значения разных знаков в зависимости от 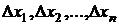, то экстремума в точке 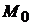нет;

если 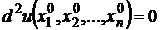для набора значений 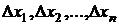, не равных нулю одновременно, то требуются дополнительные исследования.

Рассмотрим случай функции двух переменных.

Определение. Функция 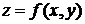имеет максимум (минимум) в точке 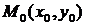, если существует такая окрестность точки 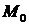, в которой для всех точек 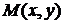отличных от 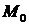, выполняется неравенство .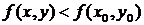

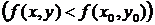Необходимое условие экстремума функции двух переменных. Если дифференцируемая функция 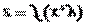достигает экстремума в точке 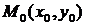, то в этой точке частные производные первого порядка равны нулю, т.е.

,

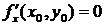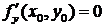. (8.1)

Введем обозначения:

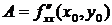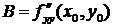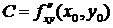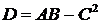, , , . (8.2)

Достаточное условие экстремума функции двух переменных.Пусть 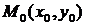- стационарная точка функции 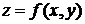и пусть в окрестности точки 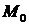функция имеет непрерывные частные производные второго порядка. Тогда:

если 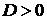, то функция 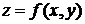имеет в точке 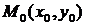экстремум, а именно максимум при 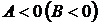и минимум при ;

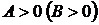если 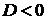, то экстремум в точке 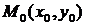отсутствует;

если 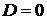, то требуются дополнительные исследования.

Рассмотрим случай функции 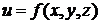трех переменных.

Критерий Сильвестра. 1) Для того, чтобы выполнялось неравенство 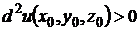при любых значениях 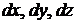, не равных нулю одновременно, необходимо и достаточно, чтобы:

, , .

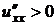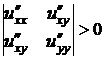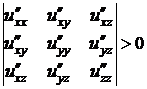2) Для того, чтобы выполнялось неравенство 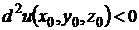при любых значениях 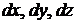, не равных нулю одновременно, необходимо и достаточно, чтобы:

, , .

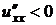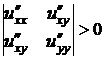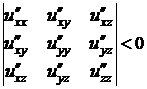Следует помнить, что все производные здесь вычислены в точке .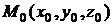

Указания к задаче 8.

Найти экстремумы функции двух переменных .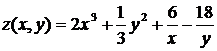

Решение.

По необходимому условию экстремума, если дифференцируемая функция 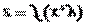достигает экстремума в точке 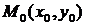, то в этой точке частные производные первого порядка равны нулю.

Найдем стационарные точки функции :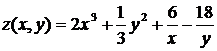

, .

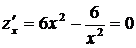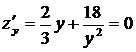Решая данную систему, получаем две стационарные точки 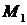(1,-3), 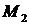(-1,-3).

Воспользуемся достаточным условием экстремума функции двух переменных. По формулам (8.2) найдем , , , .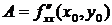

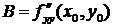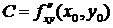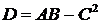Рассмотрим точку 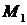(1,-3): 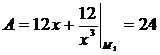, , 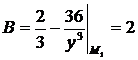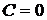. Так как 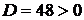, то точка 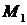(1,-3) является точкой экстремума, а именно минимума, так как 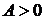. Найдем минимум функции: .

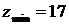Рассмотрим точку 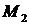(-1,-3): 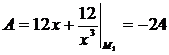, , 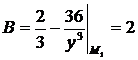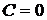. Так как 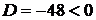, то в точке 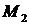(-1,-3) экстремума нет.

Условный экстремум

Пусть требуется найти экстремум функции 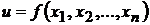при условии, что 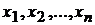связаны уравнением

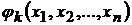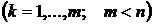, . (9.1)

Уравнения (9.1) называются уравнениями связи.

Определение.Функция 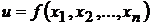имеет условный максимум (условный минимум) в точке 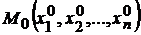, если существует такая окрестность точки 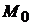, в которой для всех точек 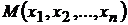( 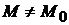), удовлетворяющих уравнениям связи, выполняется неравенство 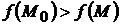(соответственно ).

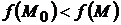Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа

,

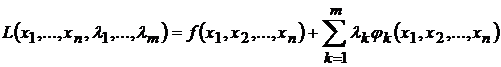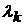
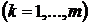называются множителями Лагранжа.

Необходимое условие условного экстремума.Если функция 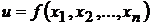имеет условный экстремум в точке 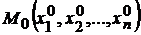, то в этой точке

.

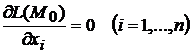Для нахождения точки, в которой возможен условный экстремум, составим систему 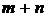уравнений:

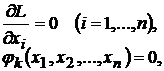, (9.2)

из которой найдем неизвестные , .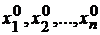

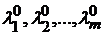Достаточное условие условного экстремума.Пусть 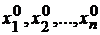, 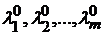решения системы (9.2), удовлетворяющие уравнениям 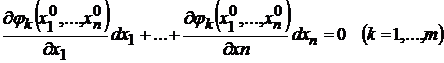при 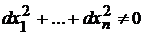. Функция 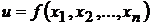имеет в точке 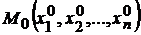условный максимум, если

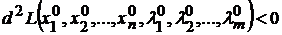
и условный минимум, если

.

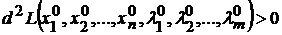В случае функции 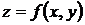двух переменных при уравнении связи 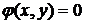функция Лагранжа примет вид

.

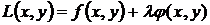Система (9.2) запишется в виде

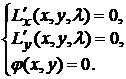
Пусть 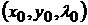- любое из решений этой системы и

.

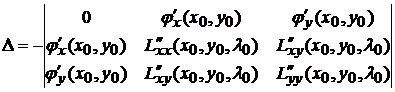Тогда, если 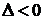, то функция 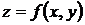имеет в точке 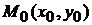условный максимум; если 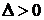– условный минимум.