Линейные операции с векторами.

1)Сложение:

Правило треугольника:

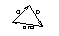
Правило параллелограмма:

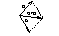
Свойства:

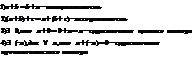
2)Разность:

Это операция, противоположная сложению векторов

3)Произведение вектора а на число λ принадлежащее R.

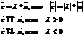
Свойства:

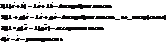
Билет 8

Векторное произведение, его геометрический смысл, критерий коллинеарности векторов.

Ориентация векторов.

Упорядоченная тройка не комплонарных векторов a,b,c называются правой, если при приведению их к общему началу, при вращении от a к b «правый винт» движется в то полупространство, куда направлен вектор с. Если же правый винт движется в полупространство, противоположное тому, куда направлен вектор с, то тройка векторов a,b,c называется левой.

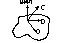
а,b,c – правая тройка векторов

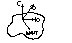
a,b,c – левая тройка векторов.

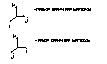
Обозначения:

A u b = [a;b]

Свойства векторного произведения векторов

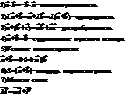
Рисунок:

Геометрический смысл векторного произведения векторов:

Тройки векторов b,c,a и c,a,b , получаются из исходной тройки a,b,c при помощи круговых перестановок и имеют с ней одинаковую ориентацию. А тройки b,a,c и a,c,b c,b,a получены другими перестановками и имеют ориентацию противоположную ориентации тройки a,b,c

Векторное произведение 2-х векторов a и b называется вектор с:

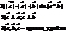
Билет 6

Линейная зависимость и независимость векторов, базис на плоскости и в пространстве, декартов базис.

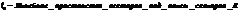
Система векторов 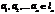называется линейно зависимой, если найдутся числа 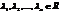, не все равные нулю одновременно и такие, что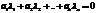

Система векторов 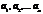, называется линейно независимой, если 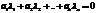тогда и только тогда, когда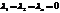
Теорема: Для того чтобы система векторов 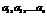была линейно зависимой, необходимо и достаточно, чтобы хотя бы один вектор системы можно представить, как линейную комбинацию остальных.

Доказательство:

1)Пусть 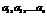линейно зависимая система, тогда существует 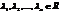и 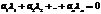и среди λ есть λ не равная нулю.

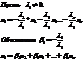
2)Обратное утверждение:

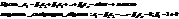
Тогда по определению 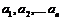- линейно зависимая.

Замечание:Любая линейно независимая система не содержит нулевого вектора.

Базис в пространстве (ЛВП)

Элементы 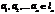называются базисом линейного векторного пространства (ЛВП), если 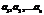- максимальная по включению линейно независимая система векторов L.

(Максимальной по включению – система линейно независимая, но добавление любого вектора делает систему линейно зависимой).

Теорема: Система векторов 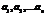образует базис ЛВП Ln, тогда и только тогда, когда любой вектор принадлежащий Ln можно представить как линейную камбинацию векторов базиса и это разложение единственно.

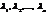- координаты в базисе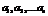

Теорема:

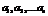- базис ó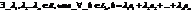

λ – координаты вектора в заданном базисе.

Базис в плоскости

Теорема: Любые 3-и вектора на плоскости линейно зависимые.

Доказательство:

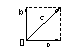
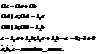
Итак:

Любые 3 вектора линейно зависимы