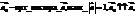Понятие числового поля, аксиомы поля

Множества натуральных чисел N={0;1;2;3;4;5;6;7;8….;n,…}

Множества целых чисел Z={ }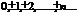

Множества рациональных чисел

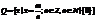
I – Множество иррациональных чисел (бесконечная, непериодическая дробь).

Множество действительных чисел R=Q U I

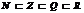
Всякая система чисел, содержащая сумму, разность и произведение 2-х своих чисел, называется кольцом

Z; Q; R; C – числовые кольца

N – Не является кольцом

Числовое кольцо называется числовым полем,если оно содержит честное 2-х своих чисел (делитель не равен нулю).

Q; R; C – числовые поля

I – не является числовым полем

Числовое поле <P+;*> P – носитель числового поля

Существуют a; b; c принадлежащие P

Выполняется 9-ть аксиом:

1) a+b=b+a коммутативность

2) (a+b)+c=a+(b+c) ассоциативность

3)Пусть существует 0 принадлежащий P, для любого a принадлежащего P => а+0=а (существование нулевого элемента).

4)Для любого а принадлежащего Р, существует (-а) принадлежащее Р => а+(-а)=0 (существование противоположного элемента).

5) a*b=b*a коммутативность умножения

6) (a*b)*c=a*(b*c) ассоциативность умножения

7) существует 1 принадлежащий P, для любого 0 принадлежащего P => а*1=1*а=а (существование единичного элемента).

8)

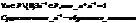
9) (a+b)*c=a*c+b*c дистрибутивность

Билет 3

Поле комплексных чисел, комплексные числа в алгебраической, тригонометрической, показательной формах.

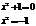
i – мнимая единица

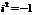
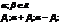
Комплексными называются числа вида z=x+iy

x=R z - действительная часть

iy=Im z – мнимая часть действительных чисел

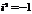
а = 5

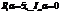
a=5+0i

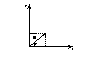
Между комплексными числами и точками плоскости существует взаимно однозначное соответствие.

z=x+iy алгебраическая форма комплексных чисел

z=x-iy Сопряженное комплексное число

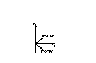
Степени мнимой единицы.

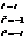
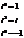
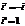
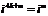
Пример.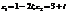

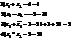
Тригонометрическаяформа

z=x+y

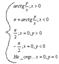
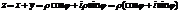- Тригонометрическая форма

Показательная форма

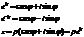
Билет 4

Теорема Безу, основная теорема алгебры

Теорема Безу

Остаток от деления многочлена 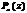на двучлен 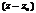равен

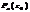
Доказательство:

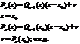
Следствие:

Для того, чтобы Pn(z) делился на 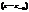без остатка, необходимо и достаточно чтобы 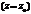было корнем многочлена.

Основная теорема алгебры (Гауса):

Всякий многочлен Pn(z) степени не меньше 1 (n>=1) имеет по крайней мере 1-н корень

Доказательство:

Билет 5

Векторы, линейные операции над ними.

Вектор – направленный отрезок, у которого есть начало и конец, длина и направление.

- нулевой вектор. 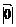= 0 – направление производное.

1)Векторы a и b коллинеарные, если они лежат на 1-й прямой или на параллельных прямых.

2)Коллинеар – сонаправленные или противоположно направленные векторы.

3)Векторы равны, если их можно совместить параллельным переносом, это значит,

что любой вектор можно считать исходящим из точку О – начало координат.

4)Векторы называются комплонарными, если они лежат в одной плоскости или параллельных плоскостях.