Множества, операции над ними, диаграммы Венна

Множества, операции над ними, диаграммы Венна

Множества - совокупность объектов, обладающих одним общим свойством, и различающими между собой.

Элементы множества:

а 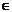А

Множеством А называется подмножество множества В, если для любого элемента а 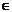А , также и а 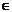В. Обозначается А 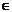В.

Два множества А и В равны, если состоят из одних и тех же элементов, то есть 2-а множества равны, если каждая из них является подмножеством другого, а именно:

А 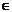В, В 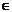А ó А=В

Множества бывают бесконечными и конечными……….

Способы задания множеств:

1)Перечисление. А={a;b;c} A={2;5;7}

2)Описание общего свойства:

A={x | P(x),k(x)};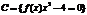

Пустое множество не содержит ни одного элемента!!!

Пустое множество является подмножеством любого множества!!!

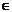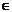Ø А; А А;

Множества всех подмножеств множества А называется булианом и обозначается ρ(А)

Например: А={a;b;c}

Число подмножества булианов =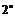

n – число элементов множества

ρ(А) – {{a};{b};{c};{a;b};{a;c};{b;c}}

Операции с множествами.

1)Объединение множеств.

Объединение множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат либо множеству А, либо множеству В.

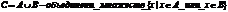
2)Пересечение множеств.

Пересечение двух множеств А и В, называют множество С, состоящее из тех и только тех элементов, которые принадлежат множеству А так и множеству В.

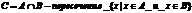
3)Разность множеств.

Разностью множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат подмножеству А и не принадлежат множеству В.

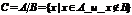
4)Дополнение множеств.

Универсальным множеством называется множество всех элементов определенного типа (все множества являются подмножествами универсального множества).

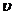- Универсум

Дополнением множества А, называется множество С, состоящее из тех и только тех элементов, которые не принадлежат А.

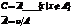
Билет 2

Билет 3

Поле комплексных чисел, комплексные числа в алгебраической, тригонометрической, показательной формах.

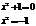
i – мнимая единица

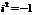
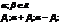
Комплексными называются числа вида z=x+iy

x=R z - действительная часть

iy=Im z – мнимая часть действительных чисел

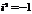
а = 5

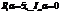
a=5+0i

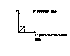
Между комплексными числами и точками плоскости существует взаимно однозначное соответствие.

z=x+iy алгебраическая форма комплексных чисел

z=x-iy Сопряженное комплексное число

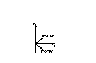
Степени мнимой единицы.

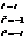
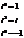
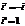
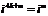
Пример.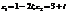

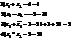
Тригонометрическаяформа

z=x+y

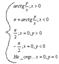
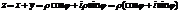- Тригонометрическая форма

Показательная форма

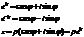
Билет 4

Теорема Безу, основная теорема алгебры

Теорема Безу

Остаток от деления многочлена 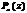на двучл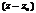ен равен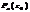

Доказательство:

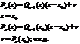
Следствие:

Для того, чтобы Pn(z) делился на 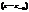без остатка, необходимо и достаточно чтобы 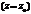было корнем многочлена.

Основная теорема алгебры (Гауса):

Всякий многочлен Pn(z) степени не меньше 1 (n>=1) имеет по крайней мере 1-н корень

Доказательство:

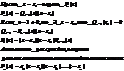
Билет 5

Билет 8

Билет 6

Базис в пространстве (ЛВП)

Элементы 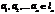называются базисом линейного векторного пространства (ЛВП), если 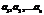- максимальная по включению линейно независимая система векторов L.

(Максимальной по включению – система линейно независимая, но добавление любого вектора делает систему линейно зависимой).

Теорема: Система векторов 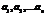образует базис ЛВП Ln, тогда и только тогда, когда любой вектор принадлежащий Ln можно представить как линейную камбинацию векторов базиса и это разложение единственно.

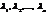- координаты в базисе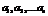

Теорема:

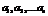- базис ó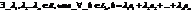

λ – координаты вектора в заданном базисе.

Базис в плоскости

Декартов базис

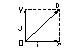
i; j – орты

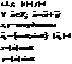
Билет 7

Билет 10

Билет 9

Смешанное произведение, его геометрический смысл, критерий компланарности векторов.

Смешанное произведение 3-х векторов:

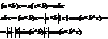
Условие комплонарности:

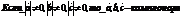
Доказательство:

Свойства смешанного произведения:

1)Если abc>0 , то тройка векторов правая

Если abc<0 , то тройка векторов левая

2) abc=bca=cab

-bac=abc=-cba=-acb

3)(λa)bc=λ(abc)

4)(a1+a2)bc=a1bc+a2bc

Площадь параллелепипеда = |abc|

Площадь пирамиды = 1/6 |abc|

В прямоугольной декартовой системе координат:

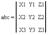
Геометрический смысл:

Модуль смешанного произведения abc равен объему параллелепипеда, построенного на векторах a,b,c а знак отвечает за ориентацию тройки .

Билет 11

Билет 12

Билет 13

Билет 14

Эллипс.

Эллипс – множество точек плоскости, сумма расстояний, которых до 2-х заданных точек (фокусов) есть величина постоянная, равная 2 а.

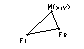
Введем ДПСК

Так, что ось Ох совпадает с фокальной осью F1F2, ось Оу – через середину F1F2.

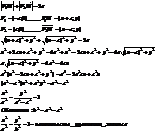
a>c

a,b-полуоси эллипса

Та ось, на которой находятся фокусы, называется большой

В доказанном случае а-большая

b-малая

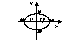
A1A2-большая ось

B1B2-малая ось

|A1A2|=2a

|B1B2|=2b

|F1F2|=2c

a^2=b^2+c^2

Если F1=F2(c=0), то эллипс является окружностью.

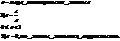
Билет 15

Гипербола.

Гипербола – это множество точек плоскости, модуль разности расстояния, которых до 2-х заданных точек (фокусов) есть величина постоянная, равная 2а.

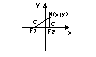
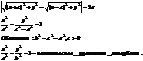
Гипербола имеет две асимптоты

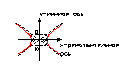
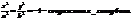
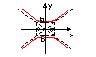
Если угол между асимптотами = п/2 , то это равносторонняя гипербола.

Если при этом асимптоты принять за оси ПДСК, то получим гиперболу показанную ниже:

y=c/x

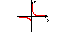
Эксцентриситет

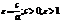
Чем меньше эксцентриситет, тем больше вытянут вспомогательный прямоугольник вдоль фронтальной оси.

Билет 16

Парабола.

Парабола – множество точек плоскости, равноудаленных от дальней точки (фокуса) и данной прямой (директриса)

Выберем ПДСК

Проведем Ох перпендикулярно директрисе, через фокус F.

Оу через середину расстояния между F и директрисой.

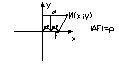
По определению p=d

|KM|=|FM|

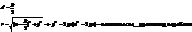
Билет 19

Билет 20

Элементарные преобразования, ранг матрицы, теорема Кронекера-Копелли.

Элементарные преобразования матриц:

1)Перестановка строк.

2)Умножение какой-либо строки на число, отличное от нуля.

3)Прибавление к одной строке другой строки, умноженное на какое-либо число.

4)Те же операции над столбцами.

И в результате всех этих преобразований, получаем матрицу, эквивалентную данной.

Ранг матрицы

Пусть в матрице А размерности m x n выбраны k строк и k столбцов, k<=m и n. Определитель матрицы, элементы которой стоят на пересечении строк и столбцов называется минором порядка k матрицы А.

Пусть все миноры матрицы А порядков, больших r, равны нулю, и при этом существует отличный от нуля минор порядка r. Число r называется рангом матрицыА. Обозначается: rangA(r,rgA) = r. Другими словами рангом матрицыА называется максимальный порядок отличного от нуля минора матрицы А. Этот минор называется базисным минором.

Способ вычисления ранга:

Привести матрицу к ступенчатому виду с помощью элементарных преобразований.

Тогда число ненулевых строк является рангом:

Пример:

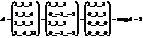
Теорема Кронекера-Копелли.

Для того чтобы система

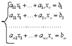
Была совместна, необходимо и достаточно, чтобы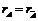

Пусть система совместна и 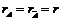- ранг системы, n-число неизвестных, m-число уравнений.

1)Пусть r<m. Будем считать без ограничения общности, что базисный минор находится в левом верхнем углу матрицы А, то есть первые r строк и первые r столбцов матрицы 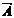линейно независимы. Тогда последние m-r уравнений можно отбросить, так как они линейно выражаются через первые r. Таким образом переходим к системе следующего вида, в котором число уравнений совпадает с рангом системы:

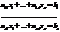
2)Если r=n, то система имеет единственное решение, которое может быть найдено, например, с помощью формул Крамера.

3)Пусть r<n (считаем, что базисный минор находится в левом верхнем углу матрицы А).

Назовем неизвестные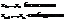

Придавая свободным неизвестным произвольные значения, получаем определенную систему относительно базисных переменных. Принимая свободные неизвестные за параметры, можно выразить базисные переменные через свободные, то есть получить общее решение системы:

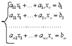
Билет 21

Метод Гаусса - универсальный способ решения линейных уравнений. Определяется принадлежность тому или иному классу (совместность, определённость). Состоит из трёх этапов1)(подготовительный)Приводим расширенную матрицу к ступенчатому виду. 2)В ходе исследования требуется выяснить :а)совместна ли система(равен ли ранг матрицы системы рангу расширенной матрицы.), б)чему равен ранг, в)какие переменные выбрать за базисные, кол-во переменных =r, но не любые могут быть базисными, а только те у которых соответствующие им столбцы ступенчатого вида не входят в базисный минор этой матрицы Рассмотрим выступающие части «ступенек». Теперь в каждой такой части выберем нулевой элемент, который с гарантией, что он существует. Эти столбцы и соответствуют переменным, которые мы выберем за базисные. Остальные переменные свободные. 3) «обратный ход». Выражаем все базисные переменные через свободные

Для этого мы должны преобразовать расширенную матрицу системы элементарными преобразованиями строк к такому виду, в котором каждый столбец, соответствующий базисной переменной, содержит только один ненулевой элемент (который мы вы­деляли на предыдущем этапе), причём этот элемент равен 1. Это преоб­разование соответствует исключению базисных переменных из "верхних уравнений". Третий этап носит название "обратный ход", потому что тре­буемые преобразования удобно проводить "снизу вверх": сначала исклю­чить последнюю базисную переменную из всех строк, кроме последней ненулевой, потом перейти к следующей снизу, и т.д. Проведя все необходимые преобразования, запишем систему линейных уравнений, соот­ветствующую полученной .расширенной матрице. Заметим, что эта си­стема эквивалентна' исходной, и в каждое уравнение входит ровно одна базисная переменная, причём с коэффициентом 1, что очень облегчает выражение базисных переменных через свободные.

Заметим, что последний этап можно также проводить и не в матрич­ном виде, а непосредственно преобразуя систему линейных уравнений, соответствующую ступенчатому виду расширенной матрицы системы. Обратите внимание, что в последнее уравнение этой системы входит только одна базисная переменная и её легко выразить через свободные. Это выражение подставим в предпоследнее уравнение и из него выразим следующую базисную переменную, и так далее, снизу вверх. В результа­те этих выражений также получим требуемое общее решение системы.

Билет 22

Критерий подпространства

Векторное пространство

Множество геометрических векторов в совокупности с введенными в предыдущем разделе линейными операциями над ними будем называть пространством геометрических векторов.

Три пространства векторов:

Множество L называется линейным векторным пространством над полем скаляров К если для любых элементов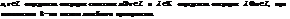

Элементами ЛВП могут быть объекты любой природы, их принято называть векторами.

Элементами числового поля являются скалярные числа.

Билет№24

Билет №25

Билет №26

Билет№27

Матрица перехода, преобразование координат вектора и матрицы линейного оператора при переходе к новому базису.

Ln – ЛВП (линейно-векторное пространство)

Известны 2 базиса: 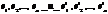Получим разложением векторов {e’} в базисе {e}

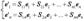
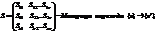
В столбцах матрицы перехода стоят координаты разложения нового базиса {e’} в старом базисе {e}

Пусть x принадлежит Ln

Формула преобразования координат при преобразовании базиса выглядит следующим образом:

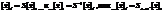
Билет№28

Билет№30

Билет№31

Квадратичные формы, преобразование матрицы квадратичной формы при переходе к новому базису.

Квадратичной формой n переменных 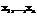называется однородный многочлен второй степени относительно этих переменных:

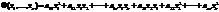* , или в матричном ви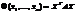де , где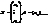

На самом деле квадратичную форму следует рассматривать как функцию, сопоставляющую каждому элементу Хевклидова пространства 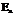некоторое вещественное число 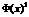. Тогда Ф в * есть ни что иное как функция от координат вектора Х.

Заметим, что матрица А, называемая матрицей квадратичной формы Ф, всегда симметрична, поскольку мы всегда можем потребовать, чтобы 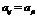, так как это коэффициенты при равных произведениях 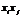и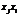

Но поскольку в записи (*) используются координаты вектора, то эта запись зависит от выбранного базиса, и, следовательно, от базиса зависит также и матрица квадратичной формы. Пусть {e} и {e’}-два базиса En, А-матрица квадратичной формы Фв базисе {e}, а А’-в базисе {e’}.Тогда (**)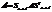

Две квадратичные формы называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования координат. Поскольку при невырожденном линейном преобразовании базис переходит в базис, то матрицы двух эквивалентных квадратичных форм будут связаны соотношением вида:(**)

Каноническим видом квадратичной формы называется эквивалентная ей квадратичная форма, содержащая только квадраты переменных: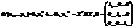

Таким образом, матрица квадратичной формы в каноническом виде диагональная. Базис, в котором квадратичная форма принимает канонический вид, называется каноническим.

Билет№32

Теорема:

Матрица линейного оператора в базисе из собственных векторов имеет диагональный вид, причем не ее диагонали стоят собственные числа оператора.

Билет№33

Матрица А называется ортогональной, если А^Т *А=А*А^Т =Е

Матрица А ортогонального оператора в некотором ортонормированном базисе называется также ортогональнойи обладает тем характеристическим свойством, что ее обратная матрица совпадает с ее транспонированной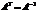

Пример:

Пусть {e},{e’} – ортонормированные базисы в евклидовом пространстве Е, 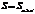Тогда по определению матрицы перехода строки матрицы S(и столбцы 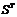)состоят их координат векторов из {e} в базисе {e’}. Докажем, что S – ортогональна, то есть 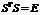, поскольку {e},{e’} – ортонормированны, то

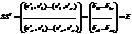
То есть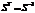

Множества, операции над ними, диаграммы Венна

Множества - совокупность объектов, обладающих одним общим свойством, и различающими между собой.

Элементы множества:

а 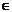А

Множеством А называется подмножество множества В, если для любого элемента а 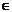А , также и а 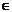В. Обозначается А 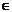В.

Два множества А и В равны, если состоят из одних и тех же элементов, то есть 2-а множества равны, если каждая из них является подмножеством другого, а именно:

А 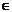В, В 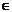А ó А=В

Множества бывают бесконечными и конечными……….

Способы задания множеств:

1)Перечисление. А={a;b;c} A={2;5;7}

2)Описание общего свойства:

A={x | P(x),k(x)};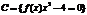

Пустое множество не содержит ни одного элемента!!!

Пустое множество является подмножеством любого множества!!!

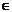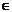Ø А; А А;

Множества всех подмножеств множества А называется булианом и обозначается ρ(А)

Например: А={a;b;c}

Число подмножества булианов =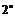

n – число элементов множества

ρ(А) – {{a};{b};{c};{a;b};{a;c};{b;c}}

Операции с множествами.

1)Объединение множеств.

Объединение множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат либо множеству А, либо множеству В.

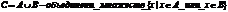
2)Пересечение множеств.

Пересечение двух множеств А и В, называют множество С, состоящее из тех и только тех элементов, которые принадлежат множеству А так и множеству В.

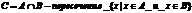
3)Разность множеств.

Разностью множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат подмножеству А и не принадлежат множеству В.

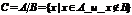
4)Дополнение множеств.

Универсальным множеством называется множество всех элементов определенного типа (все множества являются подмножествами универсального множества).

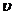- Универсум

Дополнением множества А, называется множество С, состоящее из тех и только тех элементов, которые не принадлежат А.

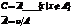
Билет 2