T2. (основная теорема интегрального исчисления)

Если f(x) непрерывна на[а,b] и F(x) первообразная для f(x),то имеет место формула Ньютона- Лейбница.

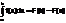
Из Т1,т.к. 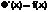, то Ф(х)-первообразная для f(x),т.к. F(x) другая первообразная, то Ф(х)= F(x)+С или

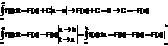
Замена переменной в определенном интеграле

Интегрирование по частям определенного интеграла

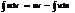
Обозначим

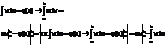
35. Несобственные интегралы с бесконечными пределами (1-го рода) и несобственные интегралы от неограниченных функций (2-го рода).

Несобственные интегралы 1-го рода

Другое название несобственных интегралов 1-го рода: интегралы с бесконечными пределами.

Несобственный интеграл от функции f(x) в пределах от a до + 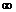определяется равенством:

⁼

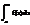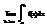
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует или равен бесконечности – расходящимся. Аналогично:

⁼ ,

⁼ .

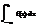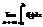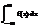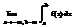Несобственные интегралы 2-го рода

Другое название несобственных интегралов 2-го рода: интегралы от разрывных (неограниченных) функций.

Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a;b] и непрерывна при a≤ 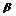<c и c<x≤b, то несобственный интеграл второго рода определяется равенством:

⁼

^{= +}

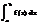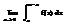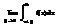^{+ (1)}

Несобственный интеграл (1) (где f(c) = 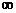,a<c<b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.

Вопрос 27 Условный экстремум. Наибольшее и наименьшее значения функции двух переменных в замкнутой области.

Условный экстремум.

Пусть , где φi — функции, заданные на . Тогда точка называется точкой условного экстремума функции f, заданной на относительно ограничений φi(x) = 0 если она является точкой обычного экстремума на множестве E.

Условный экстремум

Пусть функция

u = f(x1, x2, … , xn)

(1)

определена в некоторой области D М Rn и ее аргументы не являются независимыми переменными, а связаны k (k<n) соотношениями:

Fi(x1, x2, … , xn) = 0 (i = 1,2, … ,k).

(2)

Условия (2) называются уравнениями связи.

Пусть координаты точки M0(x10, … ,xn0) О D удовлетворяют уравнениям связи (2).

Точка M0(x10, … ,xn0) называется точкой условного максимума (минимума) функции (1) при условиях связи (2), если существует такая окрестность Oδ(M0) точки M0 , что для любой точки M(x1, … ,xn) О Oδ(M0) , координаты которой удовлетворяют уравнениям связи (2), выполняется неравенство f(M) ≤ f(M0) (f(M) ≥ f(M0)) .

Методы нахождения условного экстремума

Метод исключения переменных

Ограничимся для простоты случаем n = 2 , k = 1 , т.е. нахождением условного экстремума функции 2–х переменных.

Пусть функция z = f(x,y) определена в некоторой области D М R2 и ее аргументы связаны условием

F(x,y) = 0.

(3)

Допустим, что уравнение (3) определяет неявно функцию y(x) . Тогда можно рассматривать сложную функцию f(x,y(x)) = u(x) . Если эта функция имеет экстремум в точке x0 и y(x0) = y0 , то точка (x0,y0) является точкой условного экстремума функции f(x,y) , аргументы которой удовлетворяют уравнению связи (3).

Если уравнение связи (3) можно разрешить относительно y и перейти от неявного задания функции y(x) к явному, то отыскание условных экстремумов в рассматриваемом случае сводится к отысканию обычных (безусловных) экстремумов функции y(x) .

Метод неопределенных множителей Лагранжа

Пусть функции f(x1, x2, … , xn) и Fi(x1, x2, … , xn) (i = 1,2, … ,k) дифференцируемы в некоторой области D М Rn . Тогда задача отыскания точек условного экстремума функции f(x1, x2, … , xn) при условиях связи

Fi(x1, x2, … , xn) = 0 (i = 1,2, … ,k).

эквивалентна задаче о нахождении точек обычного (безусловного) экстремума функции Лагранжа:

L(x1,x2,:::,xn; λ1,λ2,:::,λk) = f(x1,x2,:::,xn) + λ1 · F1(x1,x2,:::,xn) +

+ λ2 · F2(x1,x2,:::,xn) + … + λk · Fk(x1,x2,:::,xm).

(4)

Схема метода Лагранжа:

1. Составляем функцию Лагранжа (4).

2. Для отыскания стационарных точек функции Лагранжа находим ее частные производные по всем аргументам

∂L

∂x1

= ∂f

∂x1

+ λ1 · ∂F1

∂x1

+ … + λk · ∂Fk

∂x1

,

… … … … …

∂L

∂xn

= ∂f

∂xn

+ λ1 · ∂F1

∂xn

+ … + λk · ∂Fk

∂xn

,

… … … … …

∂L

∂λ1

= F1(x1, x2, … , xn),

… … … … …

∂L

∂λk

= Fk(x1, x2, … , xn)

и приравниваем их к нулю.

Получаем систему (n + k) уравнений с (n + k) неизвестными:

∂f

∂x1

+ λ1 · ∂F1

∂x1

+ … + λk · ∂Fk

∂x1

= 0,

… … … … …

∂f

∂xn

+ λ1 · ∂F1

∂xn

+ … + λk · ∂Fk

∂xn

= 0,

… … … … …

F1(x1, x2, … , xn) = 0,

… … … … …

Fk(x1, x2, … , xn) = 0.

Если (x10,:::,xn0; λ10,:::,λk0) — решение этой системы, то оно определяет стационарную точку (x10,:::,xn0) функции f(x1,x2,:::,xn) при условиях связи (2), в которой функция может иметь условный экстремум.

3. Чтобы установить наличие или отсутствие условного экстремума в каждой стационарной точке M0 , нужно исследовать знак 2–го дифференциала функции Лагранжа

d2L(M0) = n ∂2L

∂xi∂xj

(M0) dxidxj

∑

i, j = 1

при значениях дифференциалов dx1, … ,dxn , не равных одновременно нулю и удовлетворяющих продифференцированным уравнениям связи

∂fi(M0)

∂x1

dx1 + … + ∂fi(M0)

∂xn

dxn = 0, i = 1,

… ,k.

Замечание. При решении практических задач во многих случаях наличие условного экстремума в стационарной точке определяется существом задачи.

Обоснование метода Лагранжа для случая n = 2 , k = 1 приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М.: Изд–во МЭИ, 2002 (стр. 170).

Геометрический смысл условного экстремума функции:

Условными экстремумами функции z = f(x,y) при F(x,y) = 0 являются ее экстремумы на линии, образующейся в сечении поверхности z = f(x,y) цилиндрической поверхностью F(x,y) = 0 .

¾¾¾¾ * * * ¾¾¾¾