Основная формула интегрального исчисления

ОСНОВНАЯ ФОРМУЛА ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ

1.Основные свойства определенного интеграла. 2.Оценки интеграла. Теорема о среднем. 3.Определенный интеграл как функция верхнего предела. 4.Вычисление определенного интеграла. Формула Ньютона-Лейбница. 5.Замена переменной и интегрирование по частям в определенном интеграле. 6.Несобственные интегралы.

На сегодняшней лекции мы продолжим изучение определенного интеграла и получим формулу для его вычисления. Как мы увидим позже, определенный интеграл равен приращению первообразной, и представляет собой постоянное число, равное площади криволинейной трапеции. Поэтому все методы вычисления неопределенного интеграла справедливы и для определенного интеграла.

Вопрос 1. Основные свойства определенного интеграла

Интеграл

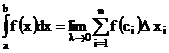(1)

был введен для случая a < b. Обобщим понятие определенного интеграла на случай, когда пределы интегрирования совпадают или нижний предел больше верхнего.

Свойство 1. .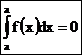

Эта формула получается из (1) при условии, что все Δx_i = 0.

Свойство 2. .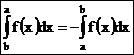

Эта формула получается из (1) при условии, что отрезок [a;b] пробегается в обратном направлении (от b к а), т.е. все Δx_i < 0.

Свойство 3. (свойство аддитивности)

Если функция f(x) интегрируема на отрезке [a;b] и a < c < b, то

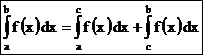. (2)

Равенство (2) справедливо при любом расположении точек а, b и с (считаем, что функция f(x) интегрируема на большем из получающихся отрезков).

Свойство 4.

Постоянный множитель можно выносить за знак определенного интеграла, т.е.

,

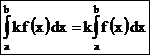где k = const.

Свойство 5.

Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций, т.е.

.

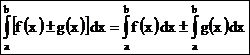Замечание

1. Свойство 5 распространяется на сумму любого конечного числа слагаемых.
2. Свойства 4 и 5 в совокупности представляют собой свойство линейности определенного интеграла.

Вопрос 2. Оценки интеграла. Теорема о среднем

Будем считать, что всюду a < b.

1. Если всюду на отрезке [a;b] функция f(x) ≥ 0, то .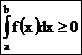

2. Если всюду на отрезке [a;b] f(x) ≥ g(x), то .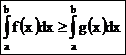

3. Для функции f(x), определенной на отрезке [a;b], имеет место неравенство .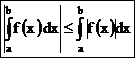

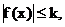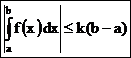В частности, если всюду на отрезке [a;b] то и .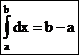

4.Если m и М – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то .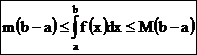

Т.2.1. (теорема о среднем)

Если функция f(x) непрерывна на отрезке [a;b], то на этом отрезке существует точка с, такая, что

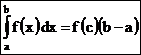. (3)

Равенство (3) называется формулой среднего значения, а величина f(c) - называется средним значением функции f(x) на отрезке [a;b].

Вопрос 5. Замена переменной и интегрирование по частям в определенном интеграле

Метод замены переменной

При вычислении определенных интегралов широко используется метод подстановки или метод замены переменной.

Т.5.1. (замена переменной в определенном интеграле)

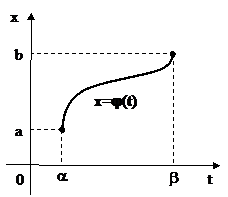
Пусть функция y = f(x) непрерывна на отрезке [a;b]. Тогда, если:

1)функция x = j(t) и ее производная x′ = j′(t) непрерывны на отрезке [a;b];

2)множеством значений функции x = j(t) является отрезок [a;b];

3)j(a) = a, j(b) = b,

то справедлива формула замены переменной в определенном интеграле:

.

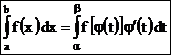Замечание

1. При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется.

2. Часто вместо подстановки x = j(t) применяют подстановку t = g(x).

3. При использовании формулы необходимо проверять выполнение перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен и неверный результат.

Пример. Вычислить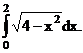

Решение

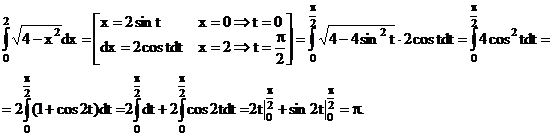
Интегрирование по частям

Т.5.2. (интегрирование по частям в определенном интеграле)

Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a;b], то справедлива формула интегрирования по частям в определенном интеграле:

.

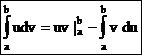Пример. Вычислить интеграл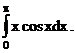

Решение

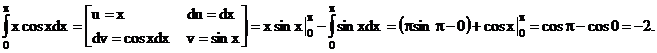
ОСНОВНАЯ ФОРМУЛА ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ

1.Основные свойства определенного интеграла. 2.Оценки интеграла. Теорема о среднем. 3.Определенный интеграл как функция верхнего предела. 4.Вычисление определенного интеграла. Формула Ньютона-Лейбница. 5.Замена переменной и интегрирование по частям в определенном интеграле. 6.Несобственные интегралы.

На сегодняшней лекции мы продолжим изучение определенного интеграла и получим формулу для его вычисления. Как мы увидим позже, определенный интеграл равен приращению первообразной, и представляет собой постоянное число, равное площади криволинейной трапеции. Поэтому все методы вычисления неопределенного интеграла справедливы и для определенного интеграла.