Группы интегралов берущихся с помощью одной и той же подстановки.
I. 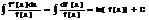
II. 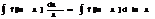
III. 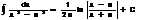
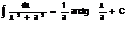
IV. 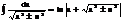
{замена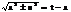 }
}
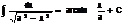
V. 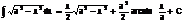

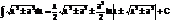
30.
Интегралы от квадратного трехчлена
1.
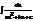 ;
; 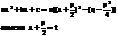
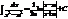
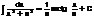
2.
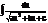
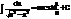
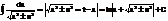
3. 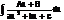
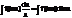
+ln (сумма 2х интегралов)
4. 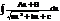
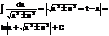
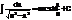
5.
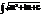
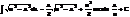
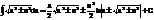
Интегрирование по частям.u=u(x) и v=v(x)-дифф-емые ф-ци), du*v=u*dv+v*du→u*dv=duv-v*du→ 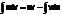 - ф-ла интегрирования по частям.
- ф-ла интегрирования по частям.
Тригонометрические подстановки:
1) 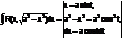 ,
,
2) 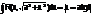
3) 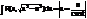
Интегрирование рациональных дробей, некоторых иррациональных функций
R(x)=P(x)/Q(x),P(x),Q(x)-многочлены степени m и n, если m<n-правильная рац.дробь, если m=>n-неправ.рац дробь
P(x)/Q(x)-неправ.рац.дробь→P(x)/Q(x)=F(x)+ P1(x) /Q(x)
Среди правильных рациональных дробей разделяют 4 вида простых или простейших дробей
1) 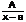 2)
2) 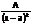
3) 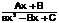 4)
4) 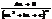
Теорема.Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей
Разложение правильной дроби на простые связано с разложением знаменателя на множители.
(m-степ, n- степ ,m<n)
Установлено, что каждому множителю 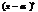 в разложении знаменателя соответствует сумма k простых дробей вида
в разложении знаменателя соответствует сумма k простых дробей вида
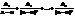 , а каждому множителю
, а каждому множителю 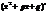 соответствует сумма s простых дробей вида:
соответствует сумма s простых дробей вида:
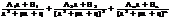
Т.о. зная разложение знаменателя на множители, мы знаем знаменатели тех простых дробей, на сумму которых разлагается данная рациональная дробь; числители этих простых дробей зависят от неопределенных коэффициентов.
1) 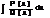 правильная или неправильная
правильная или неправильная
2)неправильная 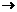 выделяем целую часть
выделяем целую часть
3)разлагаем правильную на сумму простых дробей
4) берем инт-л от каждого слагаемого
Т.о. интегралы от любой рациональной функции берутся
Интегралы от некоторых иррациональных выражений.
R ( 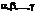 ) – рациональное ф-ция от
) – рациональное ф-ция от 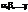
I. 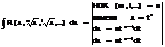
II. 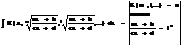
32.
Интегрирование некоторых тригонометрических ф-ций
1. 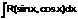
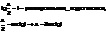
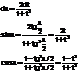
2. 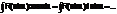
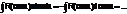
3. 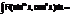 (m и n – четные)
(m и n – четные)
Формулы понижения степени:
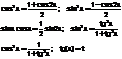
Тригонометрические подстановки:
1) 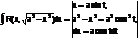 ,
,
2) 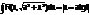
3) 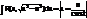
Определенный интеграл и его свойства
Пусть функция f(x) задана на отрезке [а,b] выполним следующие действия:
1)Разбить [а,b] на части 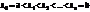
d=max 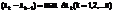
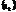 -разбиение [а,b], d-диаметр разбиения
-разбиение [а,b], d-диаметр разбиения
2) 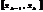 рассмотрим произвольную точку
рассмотрим произвольную точку 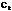 и назовем ее промежуточная, а также найдем значения f(x) в этой точке
и назовем ее промежуточная, а также найдем значения f(x) в этой точке
3)составим интегральную сумму Римана
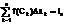
Если существует предел при d стремящимся 0 от 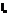 ( lim(d→0)In) то он называется определенным интегралом по Риману от f(x) по отрезку[а,b]
( lim(d→0)In) то он называется определенным интегралом по Риману от f(x) по отрезку[а,b]
И обозначается
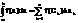
Замечания:
Предел интегрирования суммы (определенный интеграл) не зависит от способа разбиения [а,b] на части и выбора промежуточных точек
Достаточное условие интегрируемости
Т.Если f(x) непрерывна на [а,b]то она интегрируема на этом отрезке
Геометрический смысл

1)f(x)≥0 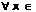 [а,b], то
[а,b], то
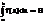
2)f(x) – знакопеременна на [а,b]
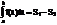
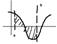
По определению полагаем
1) 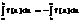 2)
2) 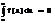
Свойства определенного интеграла:
1) 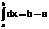
2) 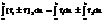
3) 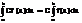
4) Если точка С разбивает[а,b] на [а,с] и [с,b], то интеграл
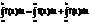
5) 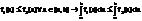
Оценка определенного интеграла
Если
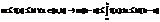

Среднее значение ф-ции на отрезке
f(x) непрерывна на[а,b], то
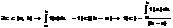
Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям для определенного интеграла.
f(x) интегрируема на[а,b], т.е.
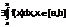 или
или 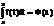
Т1.(Ньютона-Лейбница)

