Модуль 2. функции нескольких переменных

Занятие 10. Область определения ФНП. Линии и поверхности уровня. Предел и непрерывность ФНП.

Ауд.: ОЛ-7: 1792 (в), 1793 (г), 1794 (в), 1795 (а), 1796 (в), 1797 (б, в), 1788 (в), найти предел 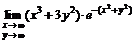, проверить функцию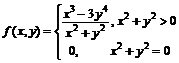

на непрерывность в точке (0; 0) или

ОЛ-6, гл. 7: 7.6, 7.8, 7.10, 7.19, 7.21 (построить линии и поверхности уровня), 7.32, 7.35, 7.44, 7.46, 7.50, 7.55.

Дома: ОЛ-7 гл. 4: 1792 (е, и), 1793 (б, в), 1794(г, ж), 1796 (а, б), 1797 (г, е), 1799 (б) или

ОЛ-6, гл. 7: 7.7, 7.9, 7.13, 7.20 (построить линии и поверхности уровня), 7.33, 7.34, 7.45, 7.47, 7.51.

Занятие 11. Частные производные 1-го порядка. Частные производные высших порядков. Дифференциал первого и второго порядка ФНП.

Ауд.: ОЛ-7: 1801–1825 (неч), 1892, 1894, 1897, 1834, 1838, 1844, 1917, 1924 или

ОЛ-6, гл. 7: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89, 7.91, 7.103, 7.105, проверить функцию 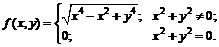на дифференцируемость в точке (0,0).

Дома: ОЛ-7: 1801–1825 (четн.), 1891, 1893, 1898, 1838, 1840, 1845, 1916, 1925 или

ОЛ-6, гл. 7: 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88, 7.90, 7.92, 7.102, 7.107.

Занятия 12-13. Производная сложной и неявной ФНП. Производная по направлению и градиент ФНП. Касательная плоскость и нормаль к поверхности.

Ауд.: ОЛ-7: 1856, 1861, 1864, 1865, 1870, 1944, 1946, 1948, 1950, 1955, 1876, 1878, 1882 (а), 1886, 1889, 1981 (а), 1982, 1985, 1986 или

ОЛ-6, гл. 7: гл. 7: 7.114, 7.119, 7.122, 7.129, 7.135, 7.141, 7.145, 7.149, 7.152, 7.229 (а), 7.233 (а), 7.232, 7.234, 7.239 (а); ОЛ-6 гл. 10: 10.31–10.43 (неч.).

Дома: ОЛ-7: 1857, 1862, 1863, 1871, 1943, 1947, 1949, 1956, 1877, 1879, 1882 (6), 1883, 1888, 1981 (б), 1984, 1987, 1990 или

ОЛ-6, гл. 7: 7.116, 7.118, 7.123, 7.130, 7.136, 7.140, 7.146, 7.150, 7.151; 7.229 (б), 7.233 (б, в), 7.235, 7.239 (б); ОЛ-6 гл. 10: 10.32–10.44 (четн.).

Занятия 14-15. Безусловный и условный экстремум ФНП.

Ауд.: ОЛ-7: 2008, 2010, 2012, 2016, 2016.1, 2021–2024, 2031 или

ОЛ-6, гл. 7: 7.187–7.195 (неч.), 7.201, 7.205, 7.214.

Дома: ОЛ-8: 2009, 2011, 2014, 2016.2, 2023, 2024, 2033 или

ОЛ-6, гл. 7: 7.187–7.195 (четн.), 7.202–7.204, 7.210–7.213.

Занятие 16. Рубежный контроль по модулю 2.

Самостоятельная подготовка

Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению контрольных работ и рубежных контролей, выполнении индивидуальных ДЗ.

Контрольные мероприятия

Модуль 1: Линейная алгебра

1. Домашнее задание №1 «Линейная алгебра»состоит из 7 задач по темам: линейные и евклидовы пространства, линейные операторы, квадратичные формы и их геометрические приложения. Сроки выполнения: выдача– 1 неделя, прием – 7 неделя.

2.Рубежный контроль № 1 по теме «Линейная алгебра», практика. Билет содержит 4-5 задач. Срок проведения – 8 неделя.

3.Рубежный контроль № 1 по теме «Линейная алгебра», теория. Задание содержит 2-3 теоретических вопроса. Срок проведения – 9 неделя.

Модуль 2. Дифференциальное исчисление функций нескольких переменных

4. Домашнее задание № 2 состоит из задач по темам: геометрическое изображение ФНП, дифференцирование сложной и неявной ФНП, дифференциалы 1 и 2 порядка, касательная плоскость и нормаль, экстремум ФНП. Сроки выполнения: выдача – 10 неделя, прием – 15 неделя.

5. Рубежный контроль № 2 по теме:Функции нескольких переменных, практика. Билет содержит 4-5 задач. Срок проведения – 16 неделя.

6. Рубежный контроль № 2 по теме:Функции нескольких переменных, теория. Задание содержит 2-3 теоретических вопроса. Срок проведения – 17 неделя.

Литература

Основная литература (ОЛ)

3. Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 336 с. (Сер. Математика в техническом университете, вып. IV).

4. Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих переменных: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 456 с. (Сер. Математика в техническом университете, вып. V).

5. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2005.

6. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с.

7. Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление. – М.: Дрофа, 2003. – 512 с.

8. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.

9. Задачи и упражнения по математическому анализу для втузов /Под ред. Б.П. Демидовича/. – М.: Астрель 2005, – 416 с.

Дополнительная литература (ДЛ)

7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматлит, 2007,– 307 с.

8. Кудрявцев Л.Д. Курс математического анализа. Т. 2. – М.: Высш. шк., 2001. – 584 с.

9. Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. –154 с.

10. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. – М.: Эдиториал УРСС, 2000. – 327 с.

11. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко Г.И. и др. – Т. 2. – М.: Эдиториал УРСС, 2000. – 184 с.

12. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. Под ред. Д.В. Беклемишева. – М.: Наука, 1987. – 496 с.

Методические пособия, изданные в МГТУ (МП)

13. Ильичев А.Т., Крапоткин В.Г., Савин А.С. Линейные операторы. Методические указания к выполнению типового расчета. – М.: МГТУ, 2003. – 36 с.

14. Пугачев О.В., Стась Г.П, Чередниченко А.В. Квадратичные формы и их геометрические приложения. Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с.

15. Гришина Г.В., Демин А.И., Михайлова О.В. Функции многих переменных. Методические указания к выполнению домашнего задания. – М.: МГТУ, 2003. – 44 с.

16. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Дифференциальное исчисление функций нескольких переменных. – М.: МГТУ, 1993. – 52 с.

17. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Прикладные задачи дифференциального исчисления функций нескольких переменных. – М.: МГТУ, 1993. – 56 с.

18. Дерябина Г.С., Чуев В.Ю. Вектор-функция нескольких переменных. – М: МГТУ, 2002, – 26 с.

19. Сидняев Н.И.. Феоктистов В.В. Линейные и евклидовы пространства. – М.: МГТУ им. Баумана, 2008.

Электронные ресурсы:

1. Павельева Е.Б., Томашпольский В.Я. Линейная алгебра. Методические указания к выполнению типового расчета (ЭУИ). – М.: МГТУ им. Баумана, 2010, http://hoster.bmstu.ru/~fn1/?page_id=30.

ЛИНЕЙНАЯ АЛГЕБРА

Дисциплина состоит из 2-х учебных модулей и экзамена

Модуль 1

Виды аудиторных занятий и самостоятельной работы	Сроки проведения или выполнения,недели	Трудоёмкость,часы	Примечание
Лекции	1-10
Упражнения	1-11
Домашние задания текущие	1-10
Контроль по модулю №1

Модуль 2

Виды аудиторных занятий и самостоятельной работы	Сроки проведения или выполнения,недели	Трудоёмкость,часы	Примечание
Лекции	11-17
Упражнения	12-17
Домашние задания текущие	11-17
Контроль по модулю №2