Модуль 2:Дифференциальные уравнения

Лекции

Лекция 1.Обыкновенное дифференциальное уравнение (ОДУ) первого порядка, его решения. Частное и общее решения. Интегральные кривые. Задача Коши дляОДУ первого порядка. Теорема Коши о существовании и единственности решения ОДУ (без вывода). Решение ОДУ первого порядка: с разделяющимися переменными, однородные ОДУ, линейные ОДУ (однородные и неоднородные), уравнения Бернулли. Геометрическая интерпретация ОДУ первого порядка. Изоклины. Геометрическое решение ОДУ с помощью изоклин.

ОЛ-2, § 1.1-1.3, 2.1, 2.2, 2.4, 3.1–3.4; ОЛ-4, гл. ХШ, § 1–5, 7–9, 3, 11, 12; ОЛ-6, гл. 1, § 1.1, 1.2, 1.3, 1.4.

Лекция 2.ОДУ n-го порядка. Частное и общее решения. Задача Коши дляОДУ n-го порядка и ее геометрическая интерпретация (при n=2). Теорема Коши о существовании и единственности решения ОДУ (без док-ва). Краевая задача. Понижение порядка некоторых типов ОДУ n-го порядка.

ОЛ-2, § 4.4, 11.1, 11.2; ОЛ-4, гл. XIII, § 16–18; ОЛ-6 гл.1, § 1.11, 1.13, 1.14.

Лекции 3-4.Линейные дифференциальные уравнения (ЛДУ) n-го порядка, уравнения однородные и неоднородные. Теорема о существовании и единственности решения. Дифференциальный оператор L[y], его свойства. Линейное пространство решений однородного ЛДУ. Линейно зависимые и независимые системы функций на отрезке. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций. Теорема о вронскиане системы линейно независимых решений однородного ЛДУ. Теорема о структуре общего решения однородного ЛДУ. Размерность пространства решений и фундаментальная система решений однородного ЛДУ. Формула Остроградского — Лиувилля и ее следствия. Понижение порядка однородного ЛДУ при известном частном решении.

ОЛ-2, § 6.1–6.3; ОЛ-4, гл. XIII, § 20; ОЛ-6, гл.1, § 1.15.

Лекции 5-6.Однородные ЛДУ с постоянными коэффициентами. Характеристическое уравнение однородного ЛДУ. Построение общего решения по корням характеристического уравнения (вывод для n=2). Неоднородные ЛДУ, структура их общего решения. Теорема о наложении частных решений. Метод Лагранжа вариации постоянных (вывод для n=2). Нахождение частного решения неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида.

ОЛ-2, § 6.2, 6.4–6.6; ОЛ-4, гл. XIII, § 21–25; ОЛ-6, гл.1, § 1.16–1.18.

Лекция7. Нормальные системы ОДУ. Задача и теорема Коши для системы ОДУ. Частное и общее решения системы ОДУ. Сведение ОДУ высшего порядка к нормальной системе ОДУ первого порядка и сведение нормальной системы ОДУ первого порядка к ОДУ высшего порядка (вывод для n=2). Первые интегралы системы. Понижение порядка системы ОДУ при помощи первых интегралов. Интегрируемые комбинации. Симметрическая форма записи нормальной автономной системы ОДУ.

ОЛ-2, § 4.1, 4.2, 6.1, 8.1–8.4; ОЛ-4, гл. XI, § 29, ОЛ-6, гл.1, § 1.19, 1.22

Лекции 8-9. Системы линейных ОДУ первого порядка. Определитель Вронского. Фундаментальная система решений. Формула Остроградского — Лиувилля. Теоремы о структуре общего решения однородной и неоднородной систем линейных ОДУ первого порядка. Метод вариации постоянных. Однородные системы линейных ОДУ с постоянными коэффициентами. Характеристическое уравнение системы. Построение общего решения по корням характеристического уравнения (вывод только для случая действительных и различных корней).

ОЛ-2, § 5.1–5.7; 6.; ОЛ-4, гл. XIII, § 30, ОЛ-6, гл.1, § 1.20-22.

Упражнения

Занятие 1.ОДУ первого порядка, его решение. Геометрическое решение ОДУ первого порядка методом изоклин. Интегрирование ОДУ с разделяющимися переменными и однородных ОДУ.

Ауд.: ОЛ-8, гл.9, §1: 9.1, 9.4, 9.9, 9.18, 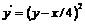(решить методом изоклин), 9.27, 9.30, 9.33, 9.35, 9.39, 9.44, 9.48, 9.49, 9.55, 9.64, 9.65 или

ОЛ-9 гл.9, §1,3,4,9: 2706, 2719, 2737, 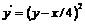(решить методом изоклин), 2742, 2744, 2746, 2748, 2750, 2770, 2772, 2775, 2848, 2852.

Дома:ОЛ-8, гл.9, §1:9.3, 9.6, 9.12, 9.20, 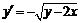(решить методом изоклин), 9.22, 9.26, 9.28, 9.34, 9.36, 9.40, 9.45, 9.47, 9.51, 9.53, 9.66 или

ОЛ-9, гл.9, §1, 3, 4, 9: 2708, 2720, 2736, 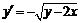(решить методом изоклин), 2743, 2745, 2747, 2769, 2771, 2773, 2873, 2834, 2840, 2857, 2874.

Занятие 2.Интегрирование линейных ОДУ первого порядка и уравнений Бернулли.

Ауд.: ОЛ-8, гл.9, § 1: 9.67, 9.72, 9.74, 9.78, 9.83, 9.88, 9.91, 9.92, 9.95 или

ОЛ-9 гл.9 §5, 9: 2785, 2787, 2789, 2791, 2793, 2794, 2847, 2850, 2854, 2881.

Дома: ОЛ-8 гл. 9 § 1: 9.68, 9.69, 9.75, 9.79, 9.80, 9.84, 9.87, 9.93, 9.94 или

ОЛ-9 гл. 9 § 5, 9: 2786, 2790, 2792, 2795, 2844, 2856, 2858, 2866.

Занятие 3. ОДУ высших порядков, основные понятия. Интегрирование уравнений, допускающих понижение порядка.

Ауд.: ОЛ-8, гл. 9, § 2: 9.202, 9.210, 9.214, 9.215, 9.216, 9.229, 9.239, 9.247, 9.251, 9.273 или

ОЛ-9, гл. 9, § 10: 2910, 2926, 2935, 2921, 2938, 2943, 2945, 2950, 2951, 2966.

Дома: ОЛ-8 гл. 9 § 2: 9.203, 9.208, 9.213, 9.220, 9.223, 9.237, 9.238, 9.248, 9.249, 9.271 или

ОЛ-9, гл. 9, § 10: 2918, 2919, 2923, 2327, 2940, 2941, 2952, 2953, 2947, 2965.

Занятие 4.Контрольная работа «Дифференциальные уравнения первого порядка».

Занятие 5.Интегрирование линейных однородных ОДУ высших порядков с постоянными коэффициентами. Фундаментальная система решений, восстановление линейного однородного ОДУ по фундаментальной системе решений.

Ауд.: ОЛ-8, гл. 9, §2: 9.286, 9.291, 9.293, 9.294, 9.324, 9.322, 9.337, 9.327, 9.333, 9.336, 9.339, 9.296, 9.300, 9.298 или

ОЛ-9, гл.9, § 11–13: 2968 (а, в, е, д), 2976, 2983, 2987, 3045, 3051, 3057, 3052, 2969 (а, в, г).

Дома: ОЛ-8, гл.9, § 2: 9.288, 9.289, 9.295, 9.325, 9.326, 9.328, 9.330, 9.332, 9.334, 9.338, 9.299, 9.301 или

ОЛ-9, гл.9, § 11–13: 2968 (б, г, д), 2981, 2982, 3055, 3056, 3048, 3049, 2969 (б).

Занятие 6.Интегрирование линейных неоднородных ОДУ с постоянными коэффициентами и специальной правой частью.

Ауд.: ОЛ-8, гл.9, § 2: 9.346, 9.349, 9.352, 9.354, 9.357, 9.360, 9.366, 9.373, 9.369, 9.371, 9.376 или

ОЛ-9 гл.9, § 12, 13: 2994 (а, в, д), 2999 3004, 3000, 3016, 3019, 3064, 3062, 3063, 3067.

Дома: ОЛ-8, гл.9, § 2: 9.347, 9.349, 9.350, 9.353, 9.355, 9.361, 9.362, 9.370, 9.372, 9.374 или

ОЛ-9, гл.9, § 12, 13: 2994 (б, г, е), 3003, 3002, 2995, 3018, 3012, 3060, 3061, 3065.

Занятие 7. Интегрирование линейных неоднородных ОДУ высшего порядка методом вариации произвольных постоянных.

Ауд.: ОЛ-8, гл. 9, § 2: 9.342, 9.344, 9.381, 9.383, 9.308, 9.310 проинтегрировать уравнения(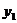-частное решение соответствующего однородного уравнения):

а) , ;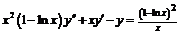

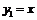б) , .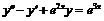

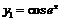в) 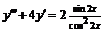или

ОЛ-9, гл. 9, § 11–13: 3033, 3035, 3038 (а), 3066, 2971, 2973, задачи а), б), в) (см. выше).

Дома: ОЛ-8, гл. 9, § 2: 9.343, 9.345, 9.385, проинтегрировать уравнения ( 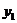-частное решение соответствующего однородного уравнения):

а) , ;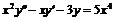

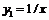б) , ;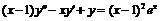

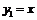в) 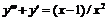или

ОЛ-9, гл. 9, § 11–13: 3032, 3034, 3037, 2972, 2974, 2975, задачи а), б), в) (см. выше).

Занятие 8.Интегрирование нормальных систем ОДУ первого порядка сведением к дифференциальному уравнению высшего порядка.

Ауд.: ОЛ-8, гл. 9, § 3: 9.402, 9.409, 9.412, 9.413, 9.417, 9.429 или

ОЛ-9 гл. 9 § 15:, 3079, 3080, 3087, 3088 (а, б), 3090.

Дома: ОЛ-8, гл.9, § 3: 9.403, 9.410, 9.414, 9.415, 9.419, 9.420, 9.428, 9.430 или

ОЛ-9, гл.9, § 15: 3078, 3083, 3085, 3088 (в), 3089.

Занятие 9.Интегрирование систем линейных однородных ОДУ с постоянными коэффициентами. Общее решение. Фундаментальная система решений.

Ауд.: ОЛ-8, гл. 9, § 3: 9.431, 9.433, 9.435.

Дома: ОЛ-8, гл.9, § 3: 9.432, 9.434, 9.436.

Занятие 10.Контроль по модулю 2 (РК №2).

Занятие 11.Интегрирование систем линейных неоднородных ОДУ первого порядка методом вариации постоянных.

Ауд.: ОЛ-8, гл. 9, § 3: 9.441, 9.443, 9.445.

Дома: ОЛ-8, гл.9, § 3: 9.442, 9.444, 9.448.

Самостоятельная подготовка

Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий, подготовке к контрольным работам и рубежным контролям.