Построение доверительного интервала для дисперсии

При построении доверительного интервала для дисперсии используется случайная величина %² (читается: "хи-квадрат"),

₂ ^ [ JC. - X | /7-1

^j 2

*, ; ^

(-1

а^{2 х}" (3.32)

которая имеет так называемое распределение Пирсона (по имени анг­лийского математика и биолога К.Пирсона), или _х²-распределение ("хи-квадрат-распределение").

Плотность распределения случайной величины %² описывается уравне­нием

4²)= А Лг¥-*?\ 0<х²<о>,

^v ' 2 -r(ir/2) (3.33)

где Г(т/2) - гамма - функция; т - число степеней свободы (при построении до­верительного интервала т = л-1).

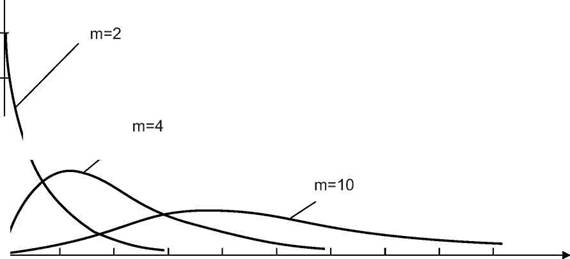
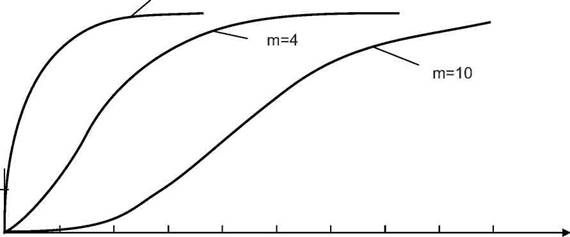
На рис.3.3 приведены кривые f(%²) для различных значений т. Эти кри­вые асимметричны, причем асимметрия особенно резко выражена при малых значениях параметра т. Так, при т =1 и %²=0 кривая уходит в бесконечность, а при т = 2 и х²=0 она достигает максимального значения, равного 0,5. При т>2 кривые имеют максимум при х²тах = т- 2. При больших значениях т (т>30) %²-

распределение переходит в нормальное со средним значением fix¹) = 4Ъп-\ и дисперсией а²=1.

Для построения доверительного интервала для дисперсии рассмотрим соотношение

Д^</<4)=^-^(3.34)

и с учетом (3.32) решим стоящее в скобках неравенство относительно а_х² :

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

P(SJ

п-1

<ст <S

п-1

^х2

Xi

) = Р₂ -Р]

(3.35)

п-1

п-1

SZ ^ OZ

х г ^{< СТ}х ^< ^х₂

±1 ± ^

(3.36)

есть доверительный интервал для дисперсии а_x² с доверительной вероятно­стью Р= Р₂ - Р₁=1-а.

f(%²) 0,5 0,4

0,3 --0,2 --0,1 --

F(%²) 1,0 -■ 0,8 --

0,6 --0,4 --0,2

a

б

m=1

х²

18 х²

Рис.3.3. Плотность распределения (а) и функция распределения (б)

X

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Как и при построении доверительного интервала для математического ожидания в технических приложениях обычно принимают Pi=a/2 и P₂=1-a/2, a a выбирают равным 0,1 или 0,05, реже 0,01.

Квантили распределения Пирсона находят по таблицам (см. [11] или табл. П.З), а в Microsoft Excel для этого используется функция ХИ20БР.

Границы доверительного интервала для среднего квадратичного откло­нения а_х находятся путем извлечения квадратного корня из значений довери­тельных границ для дисперсии.

В примере 3.1 по трем выборочным значениям 351, 370 и 365, S² _HB =97

при a = 0,05 (Pi=0,05/2=0,025 и P₂=1-0,05/2=0,975; ХИ2ОБР(0,025;2) = 7,377779 и ХИ2ОБР(0,975;2) = 0,050636) доверительный интервал для дисперсии твер­дости составит

97----- <сг2<97------- , или после вычислений 26<<т2<3880, а довери-

7,38 0,05

тельный интервал для среднего квадратичного отклонения будет равен

5 < сг <62.

Определение необходимого количества опытов при построении интервальной оценки для математического ожидания

Увеличение количества измерений (числа проб, образцов и т.п.), как вид­но из выражений (3.27) и (3.31) даже при неизменной их точности (a_x = const), может увеличить доверительную вероятность P или сузить доверительный ин­тервал ±8 для определения действительного значения измеряемой величины (математического ожидания).

Необходимое количество измерений (образцов, проб и т.п.) n для дости­жения требуемой точности 8 при заданной доверительной вероятности Р можно определить заранее в том случае, когда известно действительное значение среднеквадратичного отклонения а_х, а экспериментальные данные (измерения) подчиняются нормальному закону распределения.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Действительно, при этих допущениях число измерений можно опреде­лить из выражения (3.27)

п>

1-a/2^x

\ 5

где£ = а_х/8.

2 1-а/2

(7

X

KSj

2 1—a/2

"И²

, (3.37)

Таким образом, число измерений л определяется требуемой довери­тельной вероятностью Р =1- а и относительным (по отношению к среднеквад­ратичному отклонению) значением половины ширины доверительного интерва­ла 8, т.е. требуемой точностью определения измеряемой величины. Так, при Р=0,95, zo,975 = 1,96 и при S=G_x число измерений равно 4. При увеличении необ­ходимой точности измерений в 2 раза, т.е. сужении доверительного интервала до величины 8=(1/2)а_х, необходимое число измерений составит 16. Нетрудно заметить, что необходимое число измерений с увеличением точности возрас­тает в квадратичной зависимости.

Как правило, действительное значение среднеквадратичной ошибки (а_х) неизвестно, а имеется только ее оценка (S_x). В этом случае следует воспользо­ваться соотношением (3.31), т.е. критерием Стьюдента, и необходимое число измерений определять из соотношения

„>'*,"'S' =t2 ■ ^ 82 а,п U

^а_,^т (3.38)

где £ = S_x/S.

При расчетах по этому уравнению следует иметь в виду, что значение критерия Стьюдента зависит не только от а, но и от числа степеней свободы т, последние же определяются числом измерений. В связи с этим уравнение (3.38) следует решать методом последовательных приближений. В качестве начального приближения можно задать, в частности, число измерений, рассчи­танных по формуле (3.37). Так, если решить последнее уравнение методом по­следовательных приближений, то можно показать, что при Р=0,95 (а=0,05) для определения доверительного интервала с точностью S=S_x требуется 7 измере­ний, а с точностью 8=0,5S_x - 19. С повышением необходимой точности различие

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

в числе измерений, рассчитанных по соотношениям (3.37) и (3.38), уменьшает­ся и, как показывают расчеты, при величине 8<0,2S_x они практически совпада­ют.

В примере 3.1 доверительный интервал для математического ожидания твердости на поверхности катания головки рельса составил 8 = 24,45 (е =9,85/ 24,45« 0,4), и если бы нам было необходимо определить твердость с точностью ±10Н6 (е ~ 1), то для этого потребовалось бы еще, как минимум, четыре изме­рения (кроме уже трех имеющихся). Действительно, при е = 1 и Р=0,95 (а=0,05), как уже было отмечено, по (3.38) получается п > z²__0,05/2-(1)² =(1,96)² «4, затем

при т = 4-1 = 3 f₀,05,2 ^я 3 (СТЬЮДРАСПОБР(0,05;3) = 3,182449), по (3.27) полу-чаем n>t₀²_,05,3-1² «9; на следующей итерации f_0,05,8 ^а 2,3 (СТЬЮДРАС-

ПОБР(0,05;8) = 2,306006), л > 2,3² «5 и затем f₀,₀₅,4 ^я 2,8 (СТЬЮДРАС-ПОБР(0,05;4) = 2,776451), л > 2,8² «7.

Количество опытов, необходимых для построения доверительных интер­валов для математического ожидания при некоторых других S/S_x и Р, приведе­ны в табл. 3.1 (для Р=0,95 в скобках приведены значения, рассчитанные по формуле (3.37)).

Таблица 3.1

Необходимое количество измерений при построении доверительного интервала для математического ожидания

s/Sx	P=0,90	P=0,95	P=0,99
		7 (4)
0,5		19 (16)
0,4		27 (24)
0,3		46 (48)
0,1		387 (384)

Статистические гипотезы

Как уже видно из изложенного выше материала, при статистическом оце­нивании (т.е. при приближенном определении случайной величины) для обос-

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

нования (состоятельности, несмещенности и эффективности) выбора той или иной оценки неизвестного параметра распределения приходится высказывать предположение, что, например, случайная величина не противоречит нормаль­ному закону распределения. Кроме того, использование всех имеющихся выбо­рочных значений при расчете оценок, так или иначе, предполагает, что среди них нет грубых ошибок (резко выделяющихся значений). С еще большим коли­чеством различных предположений (гипотез) приходится сталкиваться, когда необходимо не только определять случайные величины, но и сравнивать их между собой, и тем более, когда по результатам эксперимента строится функ­ция отклика.

Статистическая гипотеза - любое предположение, касающееся неизвест­ного распределения случайной величины.

Например, специалиста интересует, удалось ли добиться повышения ме­ханической прочности окатышей при использовании новой технологии их обжи­га. Он может сформулировать следующую гипотезу: "Механическая прочность окатышей увеличилась". Эта гипотеза (нулевая гипотеза) будет подлежать про­верке в ходе проведения опытов. Кроме того, можно сформулировать и любую другую (альтернативную) гипотезу, например: "Изменения механической проч­ности не произошло" или "Механическая прочность окатышей, наоборот, даже уменьшилась".

Процесс принятия решения называется проверкой статистической гипо­тезы. Поскольку мы выдвигали гипотезу, опираясь только на случайные выбо­рочные значения, наши выводы будут носить вероятностный характер, то есть мы не можем дать точного ответа: да или нет. Можно будет лишь с некоторой долей уверенности (с некоторой вероятностью) утверждать, что данные не про­тиворечат (или противоречат) предположению.

Статистические гипотезы можно разделить на следующие группы.

1. Гипотезы о параметрах распределения. Эти гипотезы представляют собой предположение о значении некоторых параметров распределе­ния генеральной совокупности. Пусть, например, высказывается ги­потеза о том, что параметры (математическое ожидание, дисперсии) в двух выборках равны между собой. Обычно гипотезы о параметрах

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

распределения можно выдвигать, располагая достаточно большой информацией о генеральной совокупности или имея весомые основа­ния считать известным ее закон распределения.

2. Гипотезы о виде распределения. Это более общие гипотезы, они вы­двигаются в условиях недостаточной информации о генеральной со­вокупности. По выборке выдвигается гипотеза о том, соответствуют ли данные, например, нормальному закону распределения. Заметим, что проверка гипотезы о нормальности распределения может помочь при дальнейшей обработке выборки: если случайную величину доста­точно уверенно можно считать нормально распределенной, то к ней применимы все теоремы о нормальных величинах, в частности име­ется возможность построить доверительные интервалы для парамет­ров.

Нулевая гипотеза Но - гипотеза, подлежащая проверке. Это гипотеза, имеющая наиболее важное значение в проводимом исследовании. Нулевую гипотезу выдвигают и затем проверяют с помощью статистических критериев с целью выявления оснований для ее отклонения и принятия альтернативной гипотезы.

Альтернативная гипотеза Hi - каждая допустимая гипотеза, отличная от нулевой. Обычно в качестве альтернативной гипотезы принимают гипотезу вторую по значимости после основной.

Предположение, которое касается неизвестного параметра распределе­ния, когда вид распределения известен (например, закон Гаусса), называется параметрической гипотезой, а предположение, при котором вид распределения неизвестен, называется непараметрической гипотезой.

Задача исследователя заключается в том, чтобы на основе анализа опытных данных, полученных по выборке, принять ту или иную гипотезу отно­сительно свойств генеральной совокупности, используя при этом какой-либо способ (критерий) проверки высказанного предположения.

Статистический критерий - однозначно определенный способ проверки статистических гипотез.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Критерии для проверки параметрических гипотез называются параметри­ческими, а для проверки непараметрических гипотез - соответственно непара­метрическими.

Естественно, что прежде чем использовать тот или иной параметриче­ский критерий, экспериментатор должен найти способ убедиться в том, согла­суется или нет распределение исследуемой им случайной величины с тем или иным теоретическим (например, нормальным) распределением.

Критерий согласия - статистический критерий для проверки гипотезы о согласии (равенстве) распределения случайной величины исследуемой сово­купности с теоретическим распределением или гипотезы о согласии распреде­лений в двух и более совокупностях.

Как и при статистическом оценивании, любой критерий может быть по­строен только на основе тех результатов наблюдений, которые имеются в рас-поряжении исследователя, т.е. путем вычисления той или иной статистики. А как уже раннее было отмечено, любая статистика как некоторая функция слу-чайной величины (функция от результатов наблюдений) также является слу-чайной величиной.

Таким образом, статистические гипотезы всегда носят вероятностный характер. Это говорит о том, что, основываясь на той или иной статистике и принимая нулевую гипотезу в качестве рабочей (либо отвергая эту гипотезу и в качестве рабочей принимая альтернативную), исследователь может совершить ошибки. Ситуации, возникающие при проверке статистических гипотез, пред­ставлены в табл.3.2.

1. Гипотеза Н₀ верна, и она не отвергается, т.е. принятое решение от-ражает истинное положение и принимается верная гипотеза.

2. Гипотеза Н₀ верна, но она отвергается, т.е. в этом случае допущена ошибка первого рода. Ошибка первого рода - ошибка, заключающаяся в том, что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза верна. Вероятность этого события по определению равна уровню значимости а. Уровень значимости а - вероятность ошибки пер­вого рода. Так как уровень значимости задается произвольно, можно

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

снизить вероятность ошибки первого рода до сколь угодно низкого уров­ня.

3. Гипотеза Н₀ неверна, и она отвергается. Опять принятое решение от­ражает истинное положение и отвергается неверная гипотеза.

4. Гипотеза Н₀ неверна, но она не отвергается. В этом случае допущена ошибка второго рода. Ошибка второго рода - ошибка, заключающаяся в том, что принимают нулевую гипотезу, в то время как в действительности эта гипотеза неверна. Если вероятность ошибки второго рода обозначить как р, то величина 1 - Р носит название мощность критерия. Мощность критерия - вероятность того, что если верна альтернативная гипотеза, то нулевая гипотеза будет отвергнута.

Таблица 3.2 Возможные исходы при проверке статистических гипотез

Фактическая ситуация	Но - принимается	Но - отвергается
Но - верна	Правильное решение	Ошибка первого рода (а)
Н0 - не верна	Ошибка второго рода (Р)	Правильное решение

Значения применяемой для данного критерия статистики, при которых для выбранного уровня значимости отвергается нулевая гипотеза, образуют так называемую критическую область.

Критическая область со - область со следующими свойствами: если зна­чения применяемой статистики принадлежат данной области, то отвергают ну­левую гипотезу; в противном случае ее принимают.

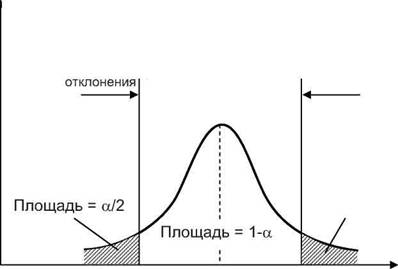
Приведенные определения намечают самую простую форму проверки статистических гипотез. Для того чтобы пояснить сущность этого метода, пред­положим, что выборочная величина 0, представляющая собой несмещенную оценку параметра ©о, имеет плотность распределения f(@). Если гипотеза, со­стоящая в том, что @=@о, верна, то функция f(@) должна попадать в среднюю область, как показано на рис.3.4. Вероятность того, что параметр 0 не будет превышать нижнего уровня @1-_а/₂,составит

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

®1-а/

Р(®^®^_/2)= Jf(@)i® = a/2.

—ос

Вероятность того, что параметр 0 превысит верхний уровень 0_а/2, равна

х

Ф>©₁-_а/₂)= Jf(@)d® = a/2.

©а/2

Следовательно, вероятность того, что параметр 0 выйдет за пределы интервала [0i-_a/2; 0_a/₂ ], составляет а. Теперь примем величину а малой, чтобы попадание параметра 0 за пределы интервала [01-_а/г; ©a/2 ] было маловероят­но. Если после извлечения выборки и определения величины 0 окажется, что она выходит за пределы интервала [0-i-_a/₂; ©а/2 ] и попадает в критическую об­ласть, то в этом случае есть серьезные основания подвергнуть сомнению спра­ведливость проверяемой гипотезы 0 = @₀. С другой стороны, если параметр 0 попадает в интервал [0i-_a/2; 0«/2 ], то в этом случае нет серьезных оснований подвергать сомнению справедливость проверяемой гипотезы, и гипотезу ра­венства 0 = 0о можно принять. Как видно из рис.3.4, ошибка первого рода до­пускается, если гипотеза верна, а параметр 0 попадает в область отклонения гипотезы. Отсюда следует, что вероятность допустить ошибку первого рода равна а, т.е. уровню значимости критерия.

f(0)

Область принятия
Область _k_____________________ ^

Площадь = а/2

отклонения

01-а/2 ©0 ©а/2

Pwc. 3.4. Области принятия и отклонения гипотезы при проверке гипотез

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

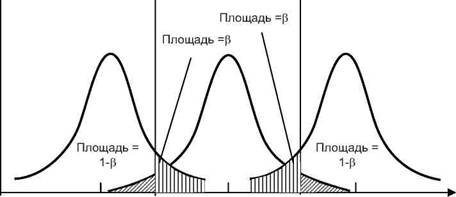
Для того чтобы найти, какова вероятность допустить ошибку второго ро­да, необходимо задать определенную величину отклонения истинного значения от гипотетического значения параметра, которое требуется определить. Пред­положим, например, что истинное значение параметра в действительности равно 0o+d или 0_o-d, как показано на рис.3.5. Если, согласно гипотезе, 0=0о, а в действительности 0=0_О ±d, то вероятность того, что 0 попадает в область принятия гипотезы, т.е. в интервал [0i-_a/2; 0_a/₂], составляет р. Это означает, что вероятность допустить ошибку второго рода при выявлении отклонения ±d от гипотетического значения 0 равна р.

▲ т(0)

0O"d ©1-a/2 ©О ©a/2 ©0+d

Рис. 3.5.Области принятия и отклонения гипотезы, соот-ветствующие ошибке второго рода при проверке гипотезы

Очевидно, что при любом заданном объеме выборки вероятность допус­тить ошибку первого рода можно сократить, уменьшив уровень значимости а. Однако при этом увеличивается вероятность допущения ошибки второго рода (снижается мощность критерия). Таким образом, в большинстве случаев нельзя добиться минимального значения вероятностей аир одновременно. Посту­пают обычно следующим образом: фиксируют вероятность а ошибки первого рода, а затем добиваются минимума вероятности р ошибки второго рода. За счет чего можно уменьшить р при фиксированном значении а? За счет пра­вильного выбора критической области: при заданной альтернативе Hi крити­ческую область выбирают таким образом, чтобы значение р (вероятность при­нять неверную гипотезу) было наименьшим из возможных. Таким образом, за-

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

дача состоит в построении наиболее мощного критерия (1- Р) при заданном уровне значимости а.

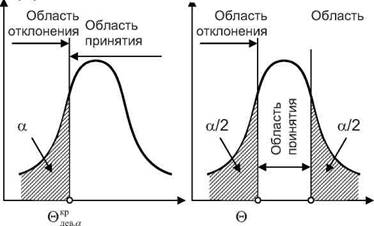
Различают односторонние и двусторонние критические области. Различ­ные варианты областей представлены на рис. 3.6.

Если хотят убедиться, что одна случайная величина строго больше или строго меньше другой, то используют одностороннюю критическую область (рис.3.6.а,б).

Таким образом, для данного случая Н₀: 0 = ©о;

Н₁⁽¹⁾ :0<0_О;

Н₁⁽²⁾0>0_О.

Если проверяют как положительные, так и отрицательные расхождения между изучаемыми величинами, то используют двусторонние критические об­ласти (рис.3.6,в)

Но : 0 = ©о ;

Н-|⁽³⁾: 0 ф 0о .

Подводя итог всему вышесказанному, алгоритм проверки любой стати­стической гипотезы в самом общем случае заключается в следующем:

1) формулирование нулевой гипотезы Н₀;

2) выбор одной из альтернативных гипотез Н/¹⁾ , Н/²⁾ , Н/³';

3) поиск критерия, по которому может быть проверена сформулированная ну­левая гипотеза Н₀;

4) расчет значения статистики, применяемой для данного критерия;

5) выбор уровня значимости а;

6) построение критической области со при выбранном уровне значимости а;

7) принятие решения: если значение статистики попало в критическую область - нулевая гипотеза отвергается, при этом вероятность ошибки (первого ро­да) не превышает выбранный уровень значимости; в противном случае -нулевая гипотеза принимается.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

а

б

в

f(0)

f(0)

отклонения И-

кр л.еъ.а/2

:(0) Область принятия	Область отклонения
\ а 1,

0кр пр,а

0^кр /,

пр,ск/2

Рис. 3.6. Критические области плотности распределения: а - правосторонняя, б - левосторонняя, в - двусторонняя

При использовании механизма статистических гипотез следует помнить, что даже в случае принятия нулевой гипотезы в 100а% вывод будет ошибоч­ным в связи со всегда имеющейся вероятностью совершить ошибку первого рода. Причем если значение статистики не попадает в критическую область, то прежде, чем принять нулевую гипотезу, необходимо оценить вероятность ошибки второго рода, т.е. рассчитать мощности критерия. Если же его величина оказывается недостаточной для решения поставленной задачи, требуется уве­личение объема опытных данных (однако поскольку при обработке эксперимен­та исследователи зачастую уже не имеют возможности увеличить объем вы­борки, то они обычно пропускают данный пункт).

Отсев грубых погрешностей

Часто даже тщательно поставленные эксперименты могут давать неод­нородные данные, поскольку в процессе эксперимента могут измениться усло­вия проведения опытов. Если экспериментатор по каким-либо причинам не уловил этих изменений, наблюдения, соответствующие разным уровням фак­торов, будут принадлежать к разным генеральным совокупностям. Данные, со­ответствующие изменившимся условиям, называют грубыми погрешностями (ошибками) или резко выделяющимися (аномальными) значениями. Грубые по­грешности появляются также при неправильной записи показаний приборов.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

В литературе приводятся сведения о том, что экспериментальные дан­ные могут содержать ~ 10% аномальных значений. Однако эти 10% могут дать сильное смещение при оценке параметров распределения, особенно для дис­персии, так как ошибки заметно отклоняются от основной группы значений, а на дисперсию особенно сильно влияют крайние члены вариационного ряда (ва­риационный ряд - результаты наблюдений, расположенные в возрастающей последовательности x-\< x₂^ x₃ ... ^ x\ ...<x_п).

В случае отсева грубых погрешностей (ошибок) нулевая гипотеза форму­лируется следующим образом:

Но :"Среди результатов наблюдений (выборочных, опытных данных) нет резко выделяющихся (аномальных) значений ".

Альтернативной гипотезой может быть либо H-i⁽¹⁾: "Среди результатов наблюдений есть только одна грубая ошибка", либо Н/²': "Среди результатов наблюдений есть две или более грубых ошиб­ки".

В литературе можно встретить большое количество различных критериев для отсева грубых погрешностей наблюдений. Обычно экспериментаторы име­ют дело с выборками небольшого объема (т.е. когда генеральная дисперсия а_х² неизвестна и оценивается по опытным данным через выборочную дисперсию S_x²), причем именно в этом случае аномальные данные имеют большой вес. Наиболее распространенными и теоретически обоснованными в этом случае являются критерий Н.В. Смирнова (используется при Н/¹⁾ ) и критерий Диксона (применим как при Н/¹⁾ , так и при Н/²⁾ ).

Критерий Н.В. Смирнова

Если известно, что есть только одно аномальное значение (альтернатив­ная гипотеза Н/¹⁾ ), то оно будет крайним членом вариационного ряда. Поэтому проверять выборку на наличие одной грубой ошибки естественно при помощи статистики

_~х-х_х

^и\ - , (3.39)

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

если сомнение вызывает

первый член вариационного ряда х_х = min x_i

или

и_п =-------- , (3.40)

s_x

если сомнителен максимальный член вариационного ряда х_п = maxx_i.

i

Этот критерий впервые был предложен Н.В. Смирновым. Он исследовал распределение статистик [(3.39), (3.40)] и составил таблицы процентных точек и_ап(квантили порядка р = 1 - а) для а = 0,1; 0,05; 0,01 при 3 ^ п < 20 [11].

При выбранном уровне значимости а критическая область для критерия Н.В. Смирнова строится следующим образом:

Ui > u_a,n ИЛИ U_n > u_a,n , (3-41)

где и_а,п- это табличные значения (см. [6] или табл. П.7).

В случае если выполняется последнее условие (статистика попадает в критическую область), то нулевая гипотеза отклоняется, т.е. выброс xi или х_п не случаен и не характерен для рассматриваемой совокупности данных, а опреде­ляется изменившимися условиями или грубыми ошибками при проведении опытов. В этом случае значение xi или х_п исключают из рассмотрения, а най­денные ранее оценки подвергаются корректировке с учетом отброшенного ре­зультата.

Критерий Диксона

В критерии Диксона применяется статистика:

• если подозрительная «чужеродная» точка имеет наибольшее значе­
ние,

х —х _■

г. . =-------- ^!LJ, (3.42)

' x n-x_J+1

• если подозрительная «чужеродная» точка имеет наименьшее значе­
ние,

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Г- ■ =

^хм - ^хх

(3.43)

^Хп_Ч~^ХХ

где х_п, x_n-i, x|+i - члены вариационного ряда xi< х₂^ хз... ^ х ...<х_п.

Диксоном были получены распределения для г-\₀, Гц, г^₂, /20, /21 и г₂2 и по­строены таблицы для а = 0,1; 0,05; 0,01 и 0,005 при 3 ^ п < 30 [11].

Статистика

п-\

х_п -х,

используется для проверки максимального или минимального члена вариаци­онного ряда (одна грубая ошибка, альтернативная гипотеза Н/¹⁾ ) при 3 < п < 7. Если при том же объеме выборки предполагается наличие двух и более резко выделяющихся значений (альтернативная гипотеза Н/²⁾ ), то используется ста­тистика г₂о-

Статистики критерия Диксона, используемые при других объемах выбор­ки, приведены в табл. 3.3.

Таблица 3.3 Статистики критерия Диксона, используемые при различных объемах выборки п

Объем выборки п	Число грубых погрешностей
одна две и более
3...7 8...10 11...13 14...30	^10 Гц /21 /22	/20 /20 /21 /22

Критическая область в критерии Диксона выглядит аналогично критерию Н.В. Смирнова и включает значения

Гц> (/"ij)a,n, (3.44)

где (гу)а,п -табличные значения (см. [11] или табл. П.8).

Рассмотрим небольшой пример.

Пример 3.3.Пирометром измеряется температура поверхности нагрето­го тела (например, прокатываемой заготовки, причем будем предполагать, что

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

температура ее видимой поверхности во всех точках одинакова). Было прове­дено шесть измерений температуры 7 °С, и получены следующие значения: 925, 930, 950, 975, 990, 1080 (п = 6, причем, как видно, все значения приведены в возрастающей последовательности, т.е. в виде вариационного ряда 7=925 < 72=930 ^ 7з =950... ^7б=1080). Можно ли значение 7б=1080 считать грубой по­грешностью, полученной, допустим, в результате неправильной регистрации показаний пирометра?

Для ответа на поставленный в этом примере вопрос предварительно вы­числим оценки параметров распределения исследуемой случайной величины Т (предполагая, что она не противоречит нормальному закону распределения):

выборочное среднее арифметическоеГ и выборочное среднее квадратичное отклонение Sj:

Т = y]T_t = (925+ 930+ 950+ 975+ 990+ 1080)/6 = 915;

2 1 V^2 1 f V^ Y 1 г„^2 2 2 2 2 2ч

S_T =------ Xi ;----- 2j ; ⁼-------- L("25 +930 +950 +975 +990 +1080 )-

n-l[_i=i n{_i=1 ) 6-1

1 ?!

— (925 + 930 + 950 + 975 + 990 + 1080) J = 3280; 6

S_T = +д/5'г ⁼ +Л/3280 = 57,27.

В электронных таблицах Microsoft Excel для этих расчетов можно было
бы использовать две статистические функции СРЗНАЧ

(925;930;950;975;990;1080) =975 и СТАНДОТКЛОН (925;930;950;975;990;1080)= 57,27128.

Теперь воспользуемся предложенным выше алгоритмом проверки стати­стических гипотез.

1. Формулируем нулевую гипотезу Н₀: "Среди значений 925; 930; 950; 975; 990; 1080 нет грубых погрешностей".

2. Исходя из условий примера 3.2, выбираем следующую альтернативную ги­потезу Н-|⁽¹⁾ : "Значение 1080 является (одной) грубой погрешностью".

3. Сформулированная нулевая гипотеза Н₀ может быть проверена по любому из приведенных в этом разделе критериев, т.е. как по критерию Н.В. Смир-

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

нова, так и по критерию Диксона (хотя в литературе могут быть найдены и другие критерии). Для начала остановимся на критерии Н.В. Смирнова.

4. Значение статистики критерия Н.В. Смирнова в примере 3.2 равно (см.
(3.40))

Т₆-Т 1080-975
и₆ =--------- =--------------- =1,83.

s_T 57,27

5. Уровень значимости а примем равным 0,05.

6. По табл. П.7 при а = 0,05 и п = 6 находим t/o,os;6 = 1,82, и с использованием (3.41) строим критическую область со: ив > Wo,o5;6, т.е. ив > 1,82.

7. Принимаем решение: поскольку значение статистики (1,83 > 1,82) попало в критическую область - нулевая гипотеза отвергается, и в качестве рабочей принимается альтернативная гипотеза, т.е. значение 1080 с вероятностью 0,95 (уровень значимости, не превышает 0,05) по критерию Н.В. Смирнова можно считать грубой погрешностью.

Интересно отметить, что если бы на этапе 5 мы приняли а = 0,01, по таб­лицам критерия Н.В. Смирнова t/o,oi;6 = 1,94 и подсчитанное значение статисти­ки при этом уровне значимости , то оно не попало бы в критическую область (1,83<1,94). Следовательно, при а = 0,01 мы не можем отвергнуть нулевую ги­потезу, т.е. по критерию Н.В. Смирнова с вероятностью 0,99 (надежностью, достоверностью) мы не можем сказать, что значение 1080 является грубой по­грешностью.

В завершение данного примера рассмотрим, как бы выглядели наши рас­четы, если на этапе 3 мы бы остановились на критерии Диксона.

4. При п = 6 и альтернативной гипотезе, что имеется только одна грубая по­грешность, в критерии Диксона используется статистика г₁₀ (см. табл. 3.3), значение которой в примере 3.2 (см. (3.43)):

Т6-Т6Ч Т6 -Т5 1080-990

0,581.

Т₆-T_0+l Т₆-Tj1080-925

5. Уровень значимости а примем равным 0,05.

6. По табл. П.8 при а = 0,05 и п = 6 находим (гю)о,о5;б = 0,560, и с использовани­ем (3.44) строим критическую область со: Гю > (гю) о,о5;б, т.е. Гю> 0,560.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

7. Принимаем решение: поскольку значение статистики (0,581 > 0,560) попало в критическую область - нулевая гипотеза отвергается, и в качестве рабочей принимается альтернативная, т.е. значение 1080 с вероятностью 0,95 и по критерию Диксона можно считать грубой погрешностью.

Заметим, однако, как и по критерию Н.В. Смирнова, высказать подобное утвер­ждение с вероятностью 0,99 по критерию Диксона мы не имеем права, посколь­ку по таблицам (г10) 0,01 ;6 = 0,698.