Выпуклость и точки перегиба графика функции
Определение. График функции f(х) называется выпуклым вверх в интервале (a;b), если он весь располагается ниже касательной проведённой к кривой в любой точке этого интервала.
Определение. График функции f(х) называется выпуклым вниз в интервале (a;b), если он весь располагается выше касательной проведённой к кривой в любой точке этого интервала.
Выпуклость вверх и выпуклость вниз определяется по знаку второй производной. Если f ''(х) < 0 в интервале (a;b), то график функции является выпуклым вверх в этом интервале; Если же f ''(х) > 0 в интервале (a;b), то график функции – выпуклый вниз.
Точка, в которой происходит смена выпуклости вверх и вниз графика функции называется точкой перегиба. В точке перегиба f ''(х) = 0 (или не существует) а знак второй производной меняется при переходе через эту точку.
Асимптоты графика функции
При построении графика функции полезно иметь представление о его поведении, когда точка графика неограниченно удаляется от начала координат.
Определение.Прямая L называется асимптотой графика функции f(х), если при стремлении точки графика к бесконечности расстояние между точкой графика функции f(х) и этой прямой стремится к нулю.
Все асимптоты делятся на два класса: вертикальные они задаются уравнением х = а, и наклонные, которые задаются уравнением у = kx + b.
Прямая х = а является вертикальной асимптотой к кривой у = f(х), если хотя бы один из пределов 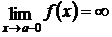 или
или 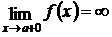 . То есть, когда точка х = а является точкой разрыва второго рода для f(х).
. То есть, когда точка х = а является точкой разрыва второго рода для f(х).
Прямая у = kх + b является наклонной асимптотой графика функции у = f(х), если существуют пределы
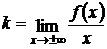 , (7.14)
, (7.14)
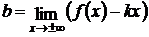 . (7.15)
. (7.15)
Соотношения (7.14) и (7.15) нужно рассматривать отдельно при х → – ∞ и при х → + ∞, так как функция может иметь при этом две разные асимптоты, не иметь одной из них или обеих.
Пример:
Найти асимптоты графика функции у = х – 2arctg x.
Решение:эта функция непрерывна на всей числовой оси, по этому вертикальных асимптот нет. Проверим существование наклонных асимптот.
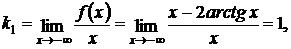

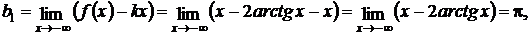
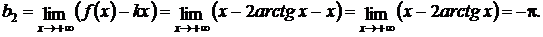
Таким образом, данная функция имеет асимптоту у = х + π при х → – ∞ и асимптоту у = х – π при х → + ∞.
Построение графика функции
Построение графика функции у = f(х) начинается с выяснения его характерных особенностей по следующей схеме:
1. нахождение области определения функции.
2. нахождение точек разрыва (если они есть), определение характера разрыва.
3. установление чётности, нечётности, периодичности.
4. нахождение точек пересечения графика функции с осями координат.
5. определение наличия асимптот и их уравнения.
6. нахождение экстремумов функции и разбиение области определения на интервалы убывания и возрастания.
7. установление точек перегиба графика функции и интервалы его выпуклости вверх и вниз.
8. построение графика функции целесообразно выполнять по его элементам, вслед за выполнением отдельных пунктов исследования. при необходимости построить несколько конкретных точек.
Пример:
Исследовать функции и построить их графики:
I. 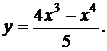
Решение: руководствуясь указанной схемой, последовательно находим:
1. Областью определения данной функции является вся числовая ось 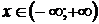 .
.
2. Так как 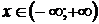 , то функция точек разрыва не имеет.
, то функция точек разрыва не имеет.
3. 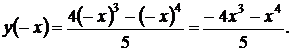 Отсюда следует, что функция не является ни четной, ни нечетной.
Отсюда следует, что функция не является ни четной, ни нечетной.
Функция не является периодической.
4. При х = 0 получим у = 0, а при у = 0 имеем уравнение 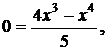 из которого находим х = 0 и х = 4. Это означает, что график функции пересекает координатные оси в точках (0; 0) и (4; 0).
из которого находим х = 0 и х = 4. Это означает, что график функции пересекает координатные оси в точках (0; 0) и (4; 0).
5. Вертикальных асимптот график функции не имеет, так как она всюду непрерывна;
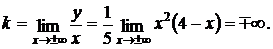
Так как k не существует, то наклонных асимптот график функции не имеет.
6. у´= 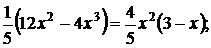
у´= 0 в точках х = 0 и х = 3, которые являются критическими. Других критических точек нет, поскольку производная у´ существует всюду.
Исследуем критические точки по первому достаточному признаку существования экстремума, записав это в виде таблицы.
| х | (– ∞; 0) | (0; 3) | (3; + ∞) | ||
| у´ | + | + | – | ||
| у | возрастает | нет экстр. | возрастает | уmax = 5,4 | убывает |
Следовательно, х = 3 – точка максимума: уmax = у(3) = 5,4.
7. у´´= 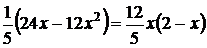 существует всюду и у´´= 0 при х = 0 и х = 2. Эти значения х могут быть абсциссами точек перегиба. Исследуем их, определяя знак у´´ слева и справа от данных точек:
существует всюду и у´´= 0 при х = 0 и х = 2. Эти значения х могут быть абсциссами точек перегиба. Исследуем их, определяя знак у´´ слева и справа от данных точек:
| х | (– ∞; 0) | (0; 3) | (2; + ∞) | ||
| у´´ | – | + | – | ||
| у | вып. вверх | перегиб у = 0 | вып. вниз | перегиб у = 3,2 | вып. вверх |
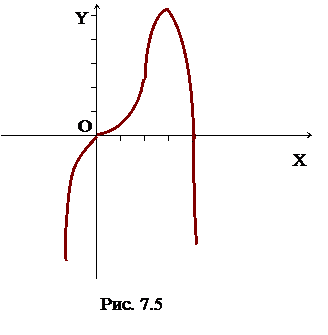 Следовательно, график функции имеет две точки перегиба (0; 0) и (2; 3,2).
Следовательно, график функции имеет две точки перегиба (0; 0) и (2; 3,2).
8. Учитывая все полученные результаты исследования, строим график функции (рис 7.5).
II. 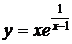
Решение: 1. Область определения данной функции
– х(–∞; 1)U( 1; +∞).
2. Функция имеет точку разрыва 2-го рода х = 1:
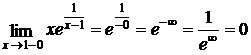 ,
, 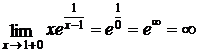 .
.
Во всех других точках числовой оси функция непрерывна.
3. 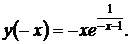 Функция не является ни четной, ни нечетной, ни периодической.
Функция не является ни четной, ни нечетной, ни периодической.
4. При х = 0 получим у = 0. Это значит, что график функции пересекает координатные оси в точке (0; 0).
5. Прямая х = 1 является вертикальной асимптотой графика функции, так как при х = 1 она имеет бесконечный разрыв.
Наклонная асимптота имеет уравнение у = kx + b, где
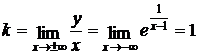 ;
;
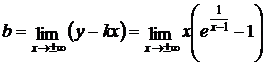 , так как при х → ∞
, так как при х → ∞ 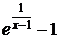 ~
~ 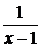 , получим:
, получим: 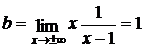 . Следовательно, график функции имеет наклонную асимптоту у = х + 1.
. Следовательно, график функции имеет наклонную асимптоту у = х + 1.
6. у´= 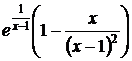 ; у´= 0 в точках х1 =
; у´= 0 в точках х1 = 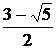 и х2 =
и х2 = 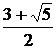 , которые являются критическими. Других критических точек нет, у´ не существует в точке х = 1, но она не является критической, так как это точка разрыва второго рода.
, которые являются критическими. Других критических точек нет, у´ не существует в точке х = 1, но она не является критической, так как это точка разрыва второго рода.
Исследуем критические точки по второму достаточному признаку существования экстремума:
у´´ 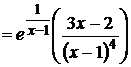 ; у´´
; у´´ 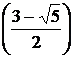 < 0, у´´
< 0, у´´ 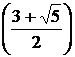 > 0.
> 0.
Следовательно, х1 = 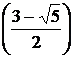 – точка максимума: уmax = у
– точка максимума: уmax = у 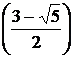 = 0,076.
= 0,076.
х2 = 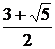 – точка минимума: уmin= у
– точка минимума: уmin= у 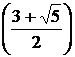 = 4,551.
= 4,551.
7. у´´ 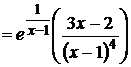 ; у´´= 0 при х =
; у´´= 0 при х = 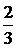 . При этом значении х может быть перегиб графика функции. Исследуем её, определяя знак у´´ слева и справа:
. При этом значении х может быть перегиб графика функции. Исследуем её, определяя знак у´´ слева и справа:
| х | (– ∞; 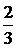 ) ) | 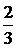 | ( 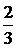 ; 1) ; 1) | (1; + ∞) | |
| у´´ | – | + | не сущест. | + | |
| у | вып. вверх | перегиб у = 0,03 | вып. вниз | вып. вниз |
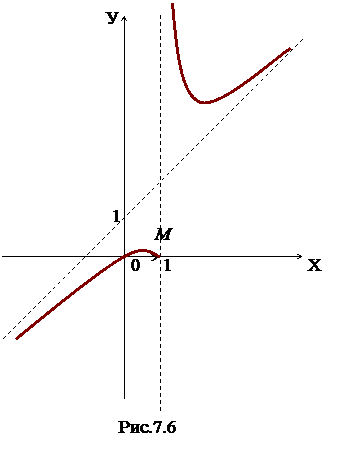
Следовательно, график функции имеет точку перегиба М( 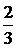 ; 0,03).
; 0,03).
8. Учитывая все полученные результаты исследования, строим график функции (рис 7.6).

 Задания для самостоятельной работы
Задания для самостоятельной работы
I. Применяя правило Лопиталя, найти пределы функций:
1. 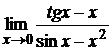 . 2.
. 2. 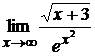 . 3.
. 3. 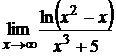 . 4.
. 4. 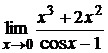
I I. Исследовать функции и построить их графики.
1. у = х3 + 3х2. 2. 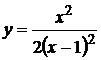 .
.  3.
3. 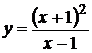 . 4. у = 16х(х – 1)3. 10.
. 4. у = 16х(х – 1)3. 10. 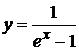 .
.
5. 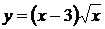 . 6.
. 6. 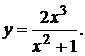 11.
11. 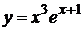 .
.
7. 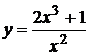 . 8.
. 8. 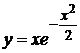 . 9.
. 9. 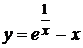 . 10.
. 10. 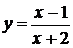
Вопросы для самоподготовки
1. Определение производной функции одной переменной.
2. Геометрический смысл производной функции одной переменной.
3. Физический смысл производной функции одной переменной.
4. Производные элементарных функций.
5. Правила дифференцирования.
6. Логарифмическое дифференцирование.
