Производные и дифференциалы функции одной переменной
Производная функции
Пусть функция у = f(х) определена на отрезке [a, b]. Возьмем произвольное значение 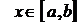 . Придадим первоначальному значению х приращение Δх, положительное или отрицательное, но такое, чтобы точка
. Придадим первоначальному значению х приращение Δх, положительное или отрицательное, но такое, чтобы точка 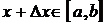 . Найдем приращение функции Δу, отвечающее приращению аргумента Δх,
. Найдем приращение функции Δу, отвечающее приращению аргумента Δх,
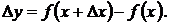
Составим разностное отношение приращения функции Δу к соответствующему приращению аргумента Δх
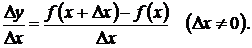
При фиксированном х это отношение является функцией от 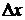 ,
,
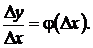
Определение.Если при 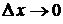 существует предел отношения
существует предел отношения 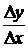 , то это предел называется производной от функции у = f(х) в данной точке х и обозначается
, то это предел называется производной от функции у = f(х) в данной точке х и обозначается 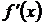 или
или 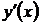 , или
, или 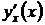 .
.
Таким образом, по определению
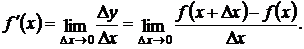 (7.1)
(7.1)
Отыскание производной называется дифференцированием функции.
Пример:
Найти производные следующих функций.
1. у = х2.
В любой точке х для любого Δх имеем
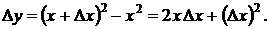
По формуле (7.1) получим 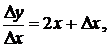 откуда
откуда 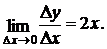
Но 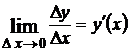 . Следовательно, функция у = х2 имеет во всякой точке х производную у΄ = 2х, то есть (х2)΄= 2х.
. Следовательно, функция у = х2 имеет во всякой точке х производную у΄ = 2х, то есть (х2)΄= 2х.
2. у = ех.
В любой точке х для любого Δх имеем
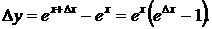
Отсюда 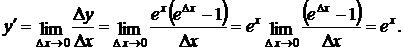
Геометрический смысл производной
Пусть f(x) непрерывная функция на в некоторой окрестности точки х1. Рассмотрим две точки А(х1;f(х1) и В(х1+Δх;f(х1+Δх1) графика этой функции (рис.7.1), через которые проходит прямая, заданная уравнением
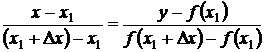 , (7.2)
, (7.2)
где х и у координаты текущей (переменной) точки прямой АВ. Преобразовав уравнение (7.2), получим
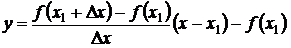 (7.3)
(7.3)
Уравнение (7.3) является уравнением секущей АВ графика функции f(x), где 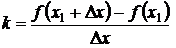 (7.4)
(7.4)
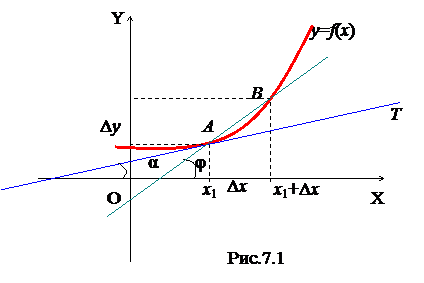 – угловой коэффициент секущей АВ.
– угловой коэффициент секущей АВ.
Точка В, двигаясь по графику функции f(x) к точке А, стремится к некоторому предельному положению – к касательной АТ. При этом касательная существует, если, как следует из уравнений (7.3) и (7.4), существует конечный предел
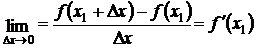 ,
,
который называется угловым коэффициентом касательной к графику функции f(x) в точке А. Из уравнения (7.3) следует уравнение касательной к кривой f(x)
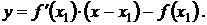
Прямая, перпендикулярная касательной к кривой f(x) в точке касания называется нормалью и имеет уравнение 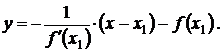
Производные элементарных функций
1. (хα)΄ = α хα –1; 10. (sh x)΄ = ch x ;
2. 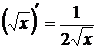 ; 11. (ch x)΄ = sh x ;
; 11. (ch x)΄ = sh x ;
3. 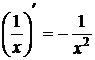 ; 12. (th x)΄ =
; 12. (th x)΄ = 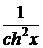 ;
;
4. (ах)΄ = ах ln a; 13. (cth x)΄ = 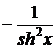 ;
;
5. (ех)' = eх ; 14. (сtg x)΄ = 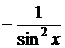 ;
;
6. 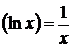 ; 11. (arcsin x)΄ =
; 11. (arcsin x)΄ = 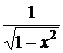 ;
;
7. (sin x)΄ = cos x ; 12. (arcсоs x)΄ = – 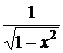 ;
;
8. (cos x)΄= – sin x ; 13. (arctg x )΄ = 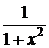 ;
;
9. (tg x)΄ = 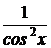 ; 14. (arcctg x )΄ =
; 14. (arcctg x )΄ = 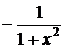 .
.
Правила дифференцирования
1. Производная постоянной величины: С '= 0.
2. Производная аргумента: x'= 1.
3. Постоянный множитель перед функцией: (Сu)´ = Сu´
4. Производная суммы (разности) функций u(х) и v(х):
(u ± v)´= u´ ± v´.
5. Производная произведения функций u(х) и v(х):
(uv)´= u´v + uv´.
6. Производная частного функций u(х) и v(х):
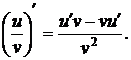
7. Производная сложной функции f(z), если z = z(у), у = y(х):
(f{z[у(х)]})' = f '(z)∙z'(у)∙y'(х).
Эти правила могут быть легко доказаны на основе теорем о пределах.
8. Дифференцирование неявной функции F(x,у) = 0 проводится дифференцированием по х обеих частей уравнения и последующего решения его относительно y'(х).
9. Дифференцирование функции, заданной параметрически.
Пусть дана функция y(х), где х и у функции параметра t, то есть
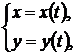 тогда
тогда 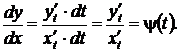
Примеры:
Найти производные от следующих функций:
1. у = sin3 x.
Решение:принимая sin x за u и пользуясь правилом дифференцирования сложной функции и формулами производных элементарных функций 1 и 7, получаем
у′ = 3 sin2 x (sin x)′ = 3 sin2 x cos x .
2. y = ln(arctg x).
Решение:в данном случае u=arctgx. Принимая правило дифференцирования сложной функции и формулы 6 и 13, получаем
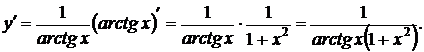
3. y = 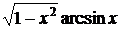 .
.
Решение:по правилу дифференцирования произведения получаем
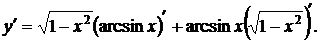
При вычислении производной от 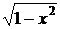 принимаем u =
принимаем u = 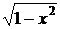 . Применяя формулу 2 и правило дифференцирования сложной функции, получаем
. Применяя формулу 2 и правило дифференцирования сложной функции, получаем
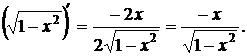
Таким образом,
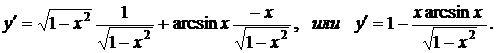
4. 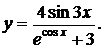
Решение:по правилу дифференцирования частного получаем
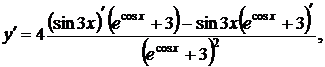 или
или
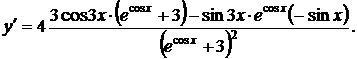
5. 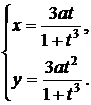
Решение:дифференцируем исходные равенства:
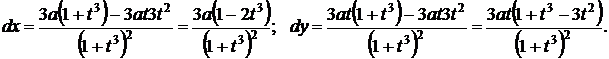 По правилу дифференцирования функций, заданных параметрически, получим
По правилу дифференцирования функций, заданных параметрически, получим