Свойства функций, непрерывных на отрезке
Теорема 1:если функция f(x) непрерывна на отрезке [a;b] и в концах его имеет значения, противоположные по знаку, то f(x) обращается в нуль по крайней мере в одной точке интервала [a;b].
Геометрически результат теоремы очевиден. Если f(а)f(b) < 0, то точки А(а; f(а)) и лежат в разных полуплоскостях, на которые ось ОХ делит плоскость ХОY. График непрерывной функции у = f(x), соединяющий эти точки, обязательно пересечет ось ОХ по крайней мере в одной точке (рис.6.2).
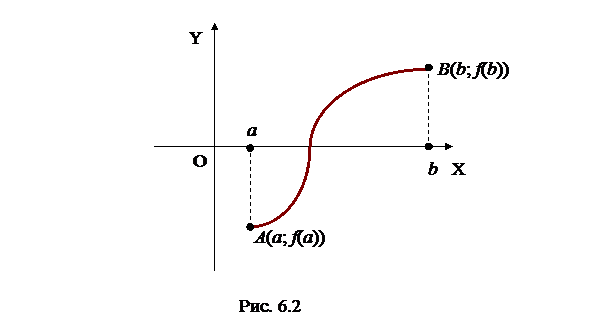
Теорема 2: Пусть функция f(x) непрерывна на отрезке [a;b], причем f(а)=А, f(b)=В. Тогда каким бы ни было число С, заключенное между числами А и В, на отрезке [a;b] найдется по крайней мере одна точка ξ такая, что f(ξ) = С.
То есть, непрерывная на отрезке [a;b] функция принимает все промежуточные значения между её значениями на концах отрезка.
Теорема 3: Если функция f(x) непрерывна на отрезке [a;b], то она ограничена на нём, то есть существует такое число К > 0, что для всех 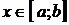 верно неравенство | f(x)| ≤ К.
верно неравенство | f(x)| ≤ К.
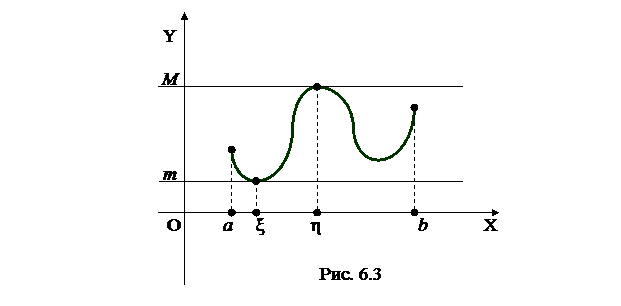
Теорема 4: Если функция f(x) непрерывна на отрезке [a;b], то она достигает на этом отрезке своих точной нижней и верхней граней, то есть на отрезке [a;b] найдутся такие точки ξ и η, что
f(ξ) = m = 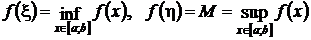 (рис. 6.3).
(рис. 6.3).
Пример:
Исследовать на непрерывность, найти точки разрыва и указать характер разрыва функции 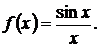
Решение:функции 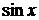 и х непрерывны в любой точке, непрерывным будет и их отношение
и х непрерывны в любой точке, непрерывным будет и их отношение 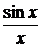 во всех точках, где х ≠ 0. В точке х = 0 данная функция не определена, и поэтому разрывна. Но существует
во всех точках, где х ≠ 0. В точке х = 0 данная функция не определена, и поэтому разрывна. Но существует 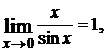 следовательно, разрыв в этой точке устранимый.
следовательно, разрыв в этой точке устранимый.
 Положим
Положим 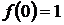 , тогда функция
, тогда функция
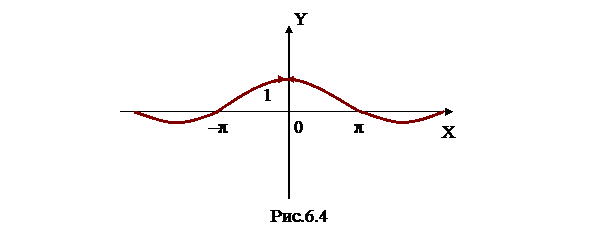
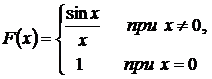 будет непрерывной в точке х = 0 (рис. 6.4).
будет непрерывной в точке х = 0 (рис. 6.4).
Пример:
Исследовать на непрерывность и найти точки разрыва функции
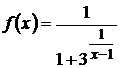 .
.
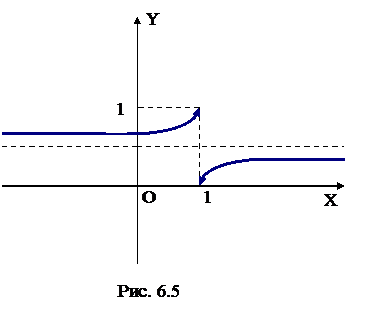 Решение:данная функция непрерывна для всех х ≠ 1(это следует из свойств непрерывных функций). Вычислим пределы слева и справа в точке х = 1. Предел слева:
Решение:данная функция непрерывна для всех х ≠ 1(это следует из свойств непрерывных функций). Вычислим пределы слева и справа в точке х = 1. Предел слева: 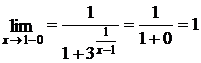 , так как
, так как 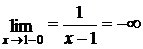 и
и
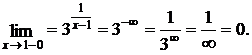
Предел справа:
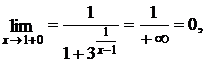
так как 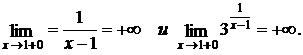
 Таким образом, пределы слева и справа существуют, но не равны, следовательно, точка х = 1 является точкой разрыва второго рода (рис. 6.5).
Таким образом, пределы слева и справа существуют, но не равны, следовательно, точка х = 1 является точкой разрыва второго рода (рис. 6.5).
Пример:
Исследовать на непрерывность и найти точки разрыва функции 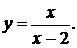
Решение:данная функция является дробно-рациональной, и поэтому она непрерывна во всех точках, в которых знаменатель отличен от нуля. В точке х = 2 функция не определена, и, следовательно, разрывна. Вычислим односторонние пределы. Предел слева: 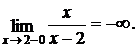
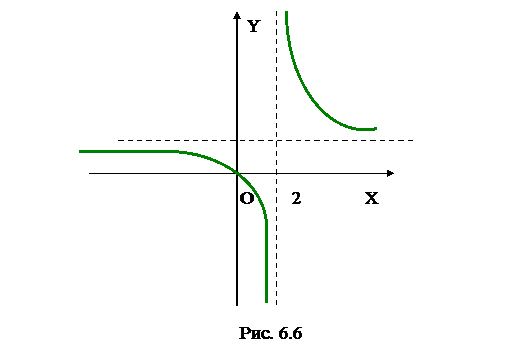
Предел справа: 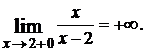 Следовательно, х = 2 – точка разрыва второго рода (рис. 6.6).
Следовательно, х = 2 – точка разрыва второго рода (рис. 6.6).
Задания для самостоятельной работы
1.Вычислить пределы:
1.1. 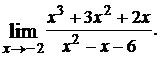 1.2.
1.2. 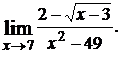 1.3.
1.3. 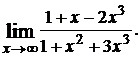 1.4.
1.4. 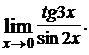 1.5.
1.5. 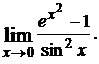 1.6.
1.6. 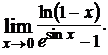 1.7.
1.7. 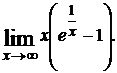 1.8.
1.8. 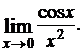 1.9.
1.9. 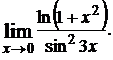 1.10.
1.10. 
2.Исследовать следующие функции на непрерывность и найти точки разрыва:
2.1. 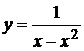 . 2.2.
. 2.2. 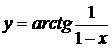 . 2.3.
. 2.3. 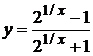 . 2.4.
. 2.4. 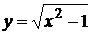 .
.
2.5. 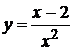 .
.
Ответы
1.1. 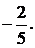 1.2.
1.2. 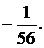 1.3.
1.3. 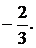 1.4.
1.4. 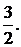 1.5.1.1.6. –1. 1.7.1. 1.8.
1.5.1.1.6. –1. 1.7.1. 1.8. 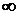 . 1.9.
. 1.9. 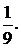 1.10.3. 2.1. В точках х = 0, х = 1 разрыв второго рода. 2.2. В точке х = 1 устранимый разрыв. 2.3. В точке х = 0 разрыв первого рода. 2.4. Точек разрыва нет, в интервале (–1; +1) функция неопределенна. 2.5. В точке
1.10.3. 2.1. В точках х = 0, х = 1 разрыв второго рода. 2.2. В точке х = 1 устранимый разрыв. 2.3. В точке х = 0 разрыв первого рода. 2.4. Точек разрыва нет, в интервале (–1; +1) функция неопределенна. 2.5. В точке 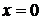 разрыв второго рода.
разрыв второго рода.
Вопросы для самоподготовки
1. Что называется отображением?
2. Частные классы отображений.
3. Область определения и график функции.
4. Элементарные функции.
5. Предел функции в точке.
6. Условие существования предела функции.
7. Свойства функций, имеющих предел.
8. Бесконечно малые функции.
9. Эквивалентные бесконечно малые функции.
10. Первый и второй классические пределы.
11. Непрерывность функции в точке.
12. Свойства непрерывных функций.
13. Свойства функций, непрерывных на отрезке.
14. Точки разрыва функции. Классификация точек разрыва.
