Сравнение бесконечно малых функций

Пусть α(х) и β(х) – бесконечно малые при х → а. Их сравнение производится по величине .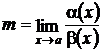

1. Если m = 0, то α(х) – бесконечно малая функция более высокого порядка, чем β(х). При сложении (вычитании) бесконечно малой функции более высокого порядка, ею можно пренебречь: β(х) ± α(х) = β(х).

2. Если m → ∞, то β(х) – бесконечно малая функция более высокого порядка, чем α(х). И тогда α(х) ± β(х) = α(х).

3. Если m = 1, то бесконечно малые функции α(х) и β(х) являются эквивалентными: .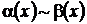

Например, первый замечательный предел

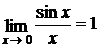(6.1)

Этот предел следует из неравенств

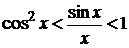, (6.2)

верных при 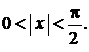Поскольку 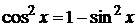и , то

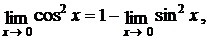
и справедливость равенства (6.1) вытекает из возможности перехода к пределам в неравенствах (6.2).

4. При других значениях m говорят, что α(х) и β(х) бесконечно малые одного порядка.

5. Если α(х) и β(х) бесконечно малые одного порядка, то [α(х)]^k – бесконечно малая k-того порядка по сравнению с β(х).

6. 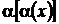бесконечно малая функция более высокого порядка, чем α(х).

При вычислении пределов возникают ситуации сравнения бесконечно малых. В этом случае говорят "имеется неопределённость вида 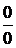". Кроме этой неопределённости существуют и другие: 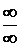, ∞ – ∞, ∞⁰, 1^∞. Вычисление пределов в этих случаях именуется раскрытием неопределённостей. При раскрытии неопределённостей используется теоремы об эквивалентных бесконечно малых функциях

Теорема 1: предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.

Теорема 2:для того чтобы две бесконечно малые функции были эквивалентными, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка по сравнению с каждой из них.

Основные эквивалентные функции при х → 0.

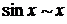; arctg x ~ x;

tg x ~ x;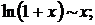

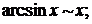
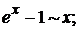
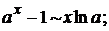
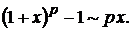
Для раскрытия неопределённостей вида ∞⁰ и 1^∞ используется значение второго замечательного предела

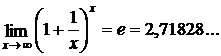или

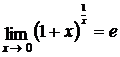– () (6.3)

Примеры:

Найти следующие пределы:

1.

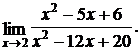
Решение: непосредственная подстановка в данное выражение предельного значения аргумента приводит к неопределенному выражению вида 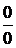. Следовательно, прежде чем перейти к пределу, необходимо данное выражение преобразовать. Числитель и знаменатель при х = 2 обращается в нуль, поэтому многочлены 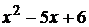и 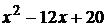делятся без остатка на бином х – 2 (теорема Безу):

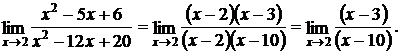
В результате непосредственной подстановки в полученное выражение предельного значения аргумента получим

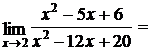
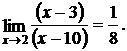
2. .

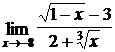Решение: неопределенность вида 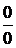. Умножим числитель и знаменатель на произведение множителей :

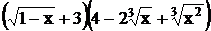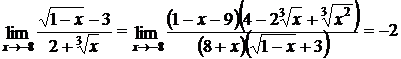
3.

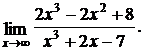
Решение: в данном случае имеем неопределенность вида 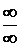. В подобного рода примерах числитель и знаменатель делят почленно на 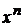, где n – степень многочлена в знаменателе. В данном примере числитель и знаменатель разделим на :

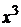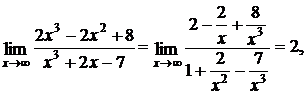
так как 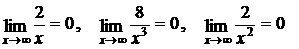и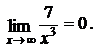

Примеры:

Найти следующие пределы:

1.

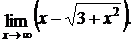
Решение: в этом примере неопределенность вида ∞ – ∞. Умножим и разделим выражение, стоящее под знаком предела, на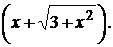

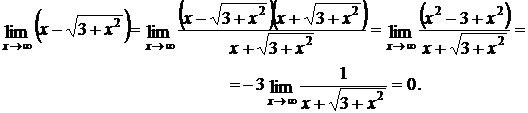
2.

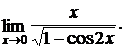
Решение: неопределенность вида 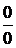. Преобразуем выражение, стоящее под знаком предела.

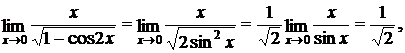
так как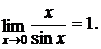

3.

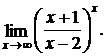
Решение: преобразуем выражение, стоящее под знаком предела, и, применив формулу (6.3), получим.

Сделав замену 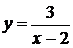, получим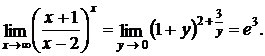

Непрерывность функции

Определение.Функция f(x) называется непрерывной в точке x = а, если:

эта функция определена в некоторой окрестности точки а;

существует предел

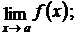
этот предел равен значению функции в точке а, то есть

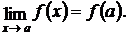
Введём обозначения: х – а = ∆х (приращение аргумента) и f(x) – f(а) = ∆у (приращение функции). Тогда условие непрерывности запишется в виде

,

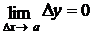то есть функция f(x) непрерывна в точке х = а тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента Δх соответствует бесконечно малое приращение функции Δу.

Если функция непрерывна в каждой точке некоторой области, то она непрерывна в этой области.

Точка х = а называется точкой разрыва, если в ней нарушается хотя бы одно из условий непрерывности функции.

Если в точке разрыва существуют лево и правосторонние пределы функции

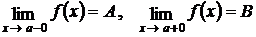и А ≠ В,

то имеет место разрыв первого рода.

Если хотя бы один из односторонних пределов не существует, то имеет место разрыв второго рода. Разрыв называется устранимым, если предел 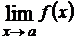существует, но функция не определена в этой точке, или функция определена в данной точке, но лево и правосторонние пределы, равные между собой, не равны значению функции в этой точке

f(а – 0) = f(а + 0) ≠ f(а).

Разность f(а + 0) – f(а – 0) даёт величину скачка функции в точке х = а.