Взаимное расположение двух прямых

За угол между двумя прямыми принимается угол между направляющими векторами этих прямых. Угол между прямыми, заданными каноническими уравнениями (3.26) определяется по формуле, аналогичной формуле угла между векторами

.

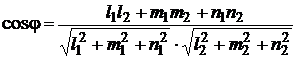Условия параллельности прямых в пространстве

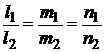
и их перпендикулярности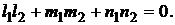

Чтобы прямые пересекались, они должны быть не параллельными и находиться в одной плоскости (условие компланарности двух прямых)

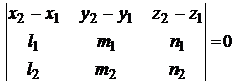
Взаимное расположение прямой и плоскости

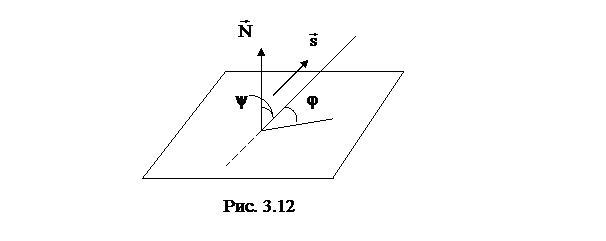
Угол между прямой 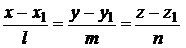и плоскостью 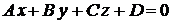(рис.3.12) определяется по формуле

.

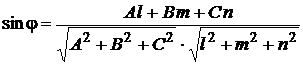Условия параллельности прямой и плоскости

,

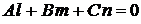а их перпендикулярности

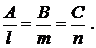
Точка пересечения прямой 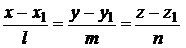и плоскости 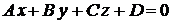находится с помощью решения системы уравнений

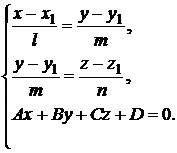
Пример:

Найти уравнения прямой, проходящей через точку А(–2;4;3) и перпендикулярно плоскости 2х – 3у – 5z – 7 = 0 и точку пересечения полученной прямой с данной плоскости.

Решение: так как искомая прямая прямая линия перпендикулярна плоскости, то за направляющий вектор прямой возьмем нормальный вектор данной плоскости: 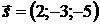. Тогда уравнения прямой будут иметь вид:

.

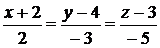Для определения координат точки С – пересечения полученной прямой и плоскости, уравнения прямой запишем в параметрическом виде и решим систему уравнений: 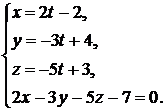Ответ: С(0;1; –2).

Задания для самостоятельной работы

1. Найти полярные координаты точки, заданной в прямоугольной системе.

1.1 А(0;1/2); 1.2 В(1;1); 1.3 C(3^1/2;1); 1.4 D(–3;3); 1.5 E(1; –3^1/2).

2. По полярным координатам точки, найти её координаты в прямоугольной системе координат.

2.1 А(2;π/3); 2.2 В(2^1/2;3π/4); 2.3 C(5; π/2); 2.4 D(3;π/6); 2.5 E(2; π/4).

3. В системе координат Оху задана точка. Найти её координаты в системе O'x'y', если оси координат повернуть на угол 45⁰, а начало координат перенести в точку О'(–2;3).

3.1 А(–2;5); 3.2 В(–6;1); 3.3 C(0;3).

4. Написать общие уравнения прямых.

4.1 у = х/3 – 1; 4.2 у = –5 х; 4.3 х/9 + у/11 = 1; 4.4 2х – у/3 = 1.

5. Вычислить угол между двумя прямыми.

5.1 у = –3/2 х + 4 и у = 2/3 х + 7; 5.2 2 х +3у = 0 и х – у + 5 = 0.

6. Найти расстояние между параллельными прямыми.

6.1 2х – 4у +7 = 0 и х – 2у + 3 = 0; 6.2 3х – 4у +1 = 0 и х =1+ 4t, y= 3t.

7. Какие кривые заданы уравнениями?

7.1 х² + у² –2х +4у– 4 = 0; 7.2 5х² + 9у² +30х–18у + 9 = 0.

8. Найти координаты вершины параболы.

8.1 у² +10х +2у = 0; 8.2 у² +6х +14у + 43 = 0; 8.3 у = х² – 6х.

9. Составить уравнение плоскости, проходящей через три точки М₁(3;–1;2), М₂(4;–1;–1), М₃(2;0;2).

10. Вычислить угол между прямой 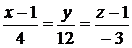и плоскостью 6х–3у+2z = 0.

Ответы

1.1 А(1/2; π/2); 1.2 В(2^1/2; π/4); 1.3 C(2; π/6); 1.4 D(18^1/2; 3π/4); 1.5 E(2; 5π/3); 2.1 А(1; 3^1/2); 2.2 В(–1; 1); 2.3 C(0; 5); 2.4 D(27^1/2/2; 3/2); 2.5 E(2^1/2; 2^1/2). 3.1 А(2^1/2; 2^1/2); 3.2 В(–18^1/2; 2^1/2); 3.3 C(2^1/2; –2^1/2). 4.1 х – 3у –3 = 0; 4.2 5х+ у = 0; 4.3 11х+ 9у–99 = 0; 4.4 6х – у –3 = 0. 5.1 90⁰; 5.2 arctg5. 6.1 0.05^1/2; 6.2 0.8. 7.1 окружность; 7.2 эллипс. 8.1 (0,1; -1); 8.2 (1; -7); 8.3 (3; -9).

9 3х + 3у + z – 8 = 0. 10 .

Вопросы для самоподготовки

1. Уравнение прямой с угловым коэффициентом.

2. Что называется полярной системой координат?

3. Как задается линия в полярных координатах?

4. Формулы перехода от декартовой системы координат к полярной.

5. Уравнение прямой на плоскости, проходящей через точку М(х₀;у₀) и

имеющей нормальный вектор .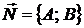

6. Канонические уравнения прямой, проходящей через точку М(х₀;у₀)

и имеющей направляющий вектор .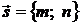

7. Нормальное уравнение прямой на плоскости.

8. Параметрические уравнения прямой на плоскости.

9. Какая линия называется окружностью?

10. Каноническое уравнение эллипса.

11. Какая линия называется гиперболой?

12. Уравнения асимптот гиперболы.

13. Каноническое уравнение параболы, симметричной

относительно оси Ох и Оу.

14. Канонические уравнения прямой в пространстве.

15. Параметрические уравнения прямой в пространстве.

16. Общее уравнение плоскости.

17. Уравнение плоскости, проходящей через три точки.

18. Уравнение плоскости в отрезках.

19. Нормальное уравнение плоскости.

20. Условия перпендикулярности двух прямых.

21. Условия перпендикулярности плоскостей.

22. Условия параллельности двух прямых.

23. Условия параллельности двух плоскостей.

24. Условия пересечения двух прямых в пространстве.

25. Угол между прямой и плоскостью.

26. Угол между двумя прямыми.

Числовые множества

Действительные числа

Определение.Прямая l, на которой выбрано начало 0, масштаб и направление, называется числовой осью.

Любому действительному числу r соответствует единственная точка числовой оси и наоборот. То есть между действительными числами и точками числовой оси установлено взаимно однозначное соответствие.

Действительные числа обладают свойствами упорядоченности: если а и b – действительные числа, то а = b, либо а < b, либо а > b. Действительные числа на числовой оси изображаются в возрастающем порядке. Множество действительных чисел обозначают R.

Если дополнить множество действительных чисел Rдвумя элементами +¥ и –¥, то получим расширенную числовую прямую и расширенное множество действительных чисел 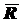, причем по определению выполняются соотношения:

1. –¥ < х < +¥, х +¥ = +¥, –¥ = – ¥, " хÎ R;

2. х (+¥) = +¥, х (– ¥) = –¥, " х > 0;

3. х (+¥) = –¥, х (– ¥) = +¥, " х < 0;

4. (+¥) + (+¥) = +¥;

5. (–¥) + (–¥) = (–¥);

6. , ;

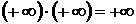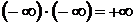7. , .

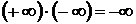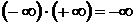Операци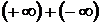и и 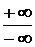неопределенны.