Взаимное расположение двух прямых на плоскости

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

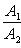
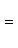
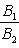
(9)

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

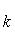
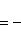
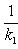
(10)

Это условие может быть записано также в виде

k₁k₂ = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0. (12)

Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда

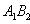
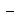
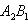
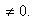
Вопрос

Расстояние от точки до прямой

Теорема.Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

.

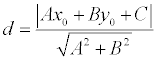Доказательство.Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М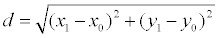₁ :

(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

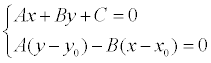
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x ₀ ) + B(y – y₀ ) + Ax₀ + By₀ + C = 0,

то, решая, получим:

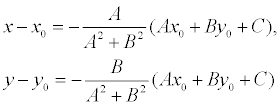
Подставляя эти выражения в уравнение (1), находим:

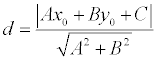
Теорема доказана.

Пример. Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k ₁ = -3; k ₂ = 2; tgφ = 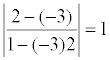; φ= p /4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k ₁ = 3/5, k₂ = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: 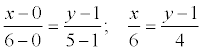; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;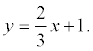

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b .

k = 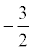. Тогда y = 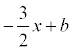. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 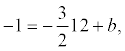откуда b = 17. Итого: .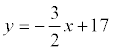

Ответ: 3 x + 2 y – 34 = 0.

Вопрос

Окружность

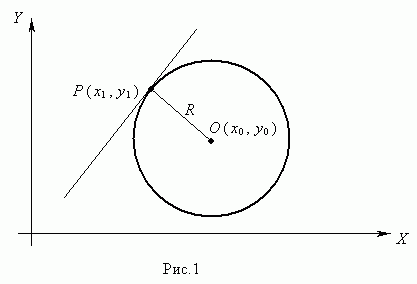
Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.

Уравнение окружности радиуса R с центром в точке О ( х₀ , у ₀ ) имеет вид:

( х – х₀ ) ² + ( у – у ₀ ) ² = R ² .

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

х ² + у ² = R ² .

Пусть Р ( х₁ , у ₁ ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:

( х₁ – х₀ ) ( х – х₀ ) + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

Условие касания прямой y = m x + k и окружности х ² + у ² = R ² :

k ² / ( 1 + m ² )= R ² .

Вопрос

Эллипс

Эллипсом ( рис.1 ) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F₁ и F₂ , называемых фокусами эллипса, есть величина постоянная.

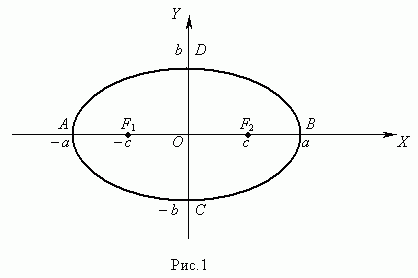
Уравнение эллипса ( рис.1 ) :

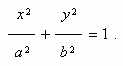
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.

Отрезок F₁F₂ = 2 с , где 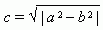, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.

Пусть Р ( х₁ , у ₁ ) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:

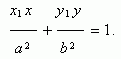
Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1 :

k ² = m ² a ²+ b ² .

Вопрос

Гипербола

Гиперболой ( рис.1 ) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F₁ и F₂ , называемых фокусами гиперболы, есть величина постоянная.

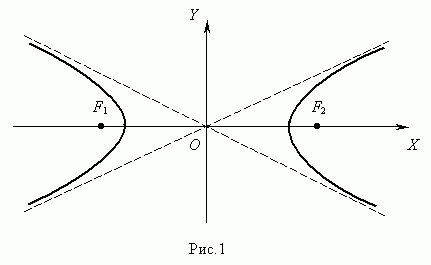
Уравнение гиперболы ( рис.1 ) :

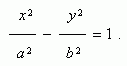
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок F₁F₂ = 2 с , где 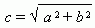, называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a , e > 1 называется эксцентриситетомгиперболы. Прямые y = ± ( b / a ) x называются асимптотами гиперболы.

Пусть Р ( х₁ , у ₁ ) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:

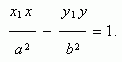
Условие касания прямой y = m x + k и гиперболы х ² / a ² – у ² / b ² = 1 :

k ² = m ² a ²– b ² .

Вопрос

Парабола

Парабола(рис. 4.16)

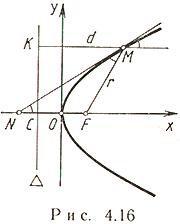
Пусть на плоскости заданы точка F и прямая 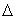, не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой 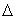. Точка F называется фокусом, прямая 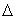- директрисой параболы; (OF) - ось, O - вершина, 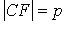- параметр, 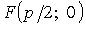- фокус, 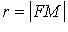- фокальный радиус.

Каноническое уравнение: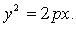

Эксцентриситет: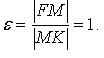

Фокальный радиус: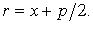

Уравнение директрисы: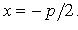

Уравнение касательной в точке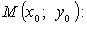

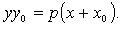
Свойство касательной к параболе: 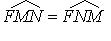(М - точка касания; N - точка пересечения касательной с осью Ox).

Уравнение нормали в точке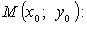

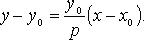
Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.

Параметрические уравнения параболы: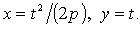

Полярное уравнение: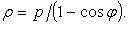

Вопрос

Векторы в пространстве

Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В - его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке A) называется противоположным вектору АВ. Вектор, противоположный вектору а, обозначается - а .

Длиной или модулем вектора АВ называется длина отрезка и обозначается |АВ|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0 . Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через e . Единичный вектор, направление которого совпадает с направлением вектора a , называется ортом вектора a и обо значается a °.

Векторы а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают a ||b .

Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Два вектор а и b называются равными (а = b ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.

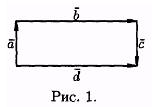
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.

На рисунке 1 векторы образуют прямоугольник. Справедливо равенство b =d , но а¹ с. Векторы а и с — противоположные, а =-с.

Равные векторы называют также свободными.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны