Аналитическая геометрия на плоскости
Прямоугольная и полярная системы координат на плоскости
Прямоугольная система координат на плоскости
В аналитической геометрии на плоскости используется две системы координат: декартова прямоугольная система и полярная система.
Декартовая прямоугольная система координат имеет линейную единицу длины и две взаимно перпендикулярные оси – ось абсцисс (ох) и ось ординат (Оу). Точка их пересечения О называется началом координат. Оси координат делят плоскость на 4 четверти, как это показано на рис. 3.1.
М(x,y) – произвольная точка. Точки МX и МY – проекции точки М на оси Ох и Оу. Отрезки ОМX = х и ОМY = у – координаты точки М. Если на плоскости даны две точки: М(x1;y1) и N(x2;y2), то расстояние d между ними вычисляется по формуле

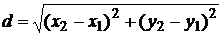 .
.
В частности, расстояние 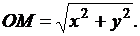
Если ∆АВС задан координатами своих вершин А(x1;y1), В(x2;y2) и С(x3;y3) , то его площадь  вычисляется по формуле:
вычисляется по формуле:
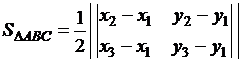 – (3.1)
– (3.1)
Равенство (3.1) получается из формулы 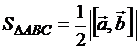 , если учесть, что координаты
, если учесть, что координаты 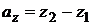 и
и 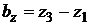
у векторов 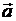 и
и 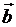 равны нулю.
равны нулю.
Полярная система координат
Полярные координаты определяются заданием точки О, называемой полюсом и луча ОА, исходящего из полюса и называемого полярной осью l. На полярной оси задается единица измерения.
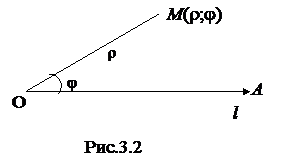 Полярными координатами произвольной точки М (рис.3.2) называются числа
Полярными координатами произвольной точки М (рис.3.2) называются числа 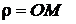 и
и 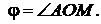 Угол, откладываемый против хода часовой стрелки, принято считать положительным (
Угол, откладываемый против хода часовой стрелки, принято считать положительным ( 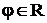 ). Главные значения полярного угла определяются неравенством: –p < j £ +p.
). Главные значения полярного угла определяются неравенством: –p < j £ +p.
первая координата r называется полярным радиусом, вторая j – полярным углом.
Совмещение систем координат
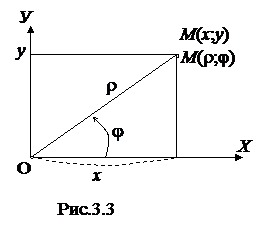 Для одновременного рассмотрения декартовой и полярной систем координат принято:
Для одновременного рассмотрения декартовой и полярной систем координат принято:
1) пользоваться одним и тем же масштабом;
2) совмещать полярный полюс с началом координат, а полярную ось с осью Ох.
Переход от одних координат к другим (рис.1.3) производится по формулам:
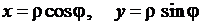 ,
,
где 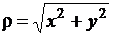 ,
, 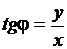 ,
,
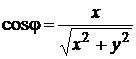 ,
, 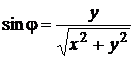 .
.
Пример:
Построить треугольник и вычислить его площадь, если вершины 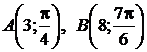 и
и 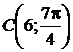 заданы в полярных координатах.
заданы в полярных координатах.
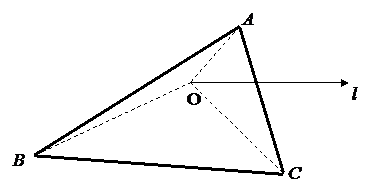 Решение:построим данный треугольник в полярной системе координат.
Решение:построим данный треугольник в полярной системе координат.
Для определения площади треугольника по формуле (3.1) координаты точек А, В и С из полярной системы координат переведем в декартовую. Для точки А получим:
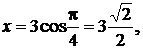
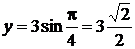 ,
,
то есть 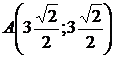 . Точки
. Точки 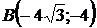 и
и 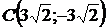 .
.
Площадь треугольника АВС по формуле (3.1) равна:
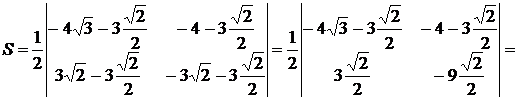
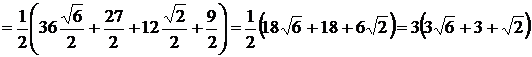 (кв.ед.).
(кв.ед.).
Пример:
Уравнение линии 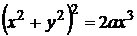 перевести в полярную систему координат и построить.
перевести в полярную систему координат и построить.
Решение:введем полярные координаты:
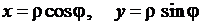 .
.
Уравнение линии примет вид 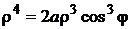 , или
, или 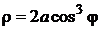 . Так как
. Так как 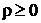 , то
, то 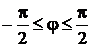 . По заданным значениям φ вычислим ρ.
. По заданным значениям φ вычислим ρ.
| φ | 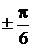 | 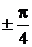 | 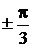 | 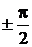 | |
| ρ | 2а | 1,3а | 0,7а | 0,25а |
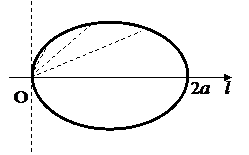 По полученным значениям φ и ρ построим линию в полярной системе координат.
По полученным значениям φ и ρ построим линию в полярной системе координат.
Линии на плоскости
Уравнением линии в заданной системе координат называется равенство f(x,y) = 0, которому удовлетворяют координаты каждой точки, принадлежащей этой линии, и не удовлетворяют координаты любой точки не принадлежащие ей. Линию можно представить себе как траекторию движущейся («текущей») точки М. В связи с этим координаты (х;у) точки М называют часто текущими координатами. Уравнение линии, связывая текущие координаты, определяет общее свойство (геометрическое, физическое и др.), присущее всем точкам этой линии.
Существует и другой способ задания линии − параметрический. В этом случае текущие координаты (х;у) точки М выражаются в виде функции
х = ϕ(t), y = ψ(t) (3.2)
некоторого параметра t. Параметр t может играть роль времени, угол поворота вокруг какой-либо фиксированной точки и т.д. Каждому фиксированному значению параметра t по формулам (3.2) соответствует определенная точка М(х;у) линии, при изменении t пробегающая всю линию. Если из двух равенств (3.2) исключить параметр t, то получится уравнение линии в виде f(x,y) = 0.
Прямая линия на плоскости
В декартовой системе координат каждая прямая определяется уравнением первой степени и, наоборот, каждое уравнение первой степени определяет прямую линию. Существует несколько видов уравнения прямой линии.
Уравнение вида 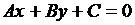 (3.3) называется общим уравнением прямой.
(3.3) называется общим уравнением прямой.
Решим уравнение (3.3) относительно у
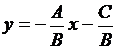 ,
,
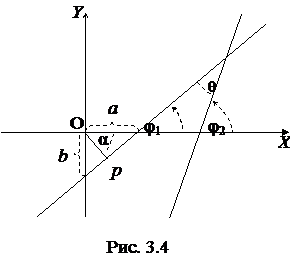 и, обозначая
и, обозначая 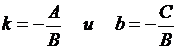 , получим уравнение прямой линии с угловым коэффициентом
, получим уравнение прямой линии с угловым коэффициентом
y = kx + b (3.4)
Приравнивая к нулю поочерёдно у и х, можно определить координаты точек пересечения прямой с осями координат (рис.3.4.) и установить геометрический смысл коэффициентов k и b.
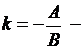 угловой коэффициент (тангенс угла наклона прямой с положительным направлением оси Ох).
угловой коэффициент (тангенс угла наклона прямой с положительным направлением оси Ох).
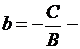 отрезок, отсекаемый прямой на осиОу (величина отрезка, отсекаемого прямой на оси Оу, считая от начала координат).
отрезок, отсекаемый прямой на осиОу (величина отрезка, отсекаемого прямой на оси Оу, считая от начала координат).
Если прямая проходит через точку М(х1;у1), то координаты этой точки должны удовлетворять уравнению (3.4), то есть 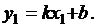 Вычтя это уравнение из уравнения (3.4), получим уравнение прямой, проходящей через точку М с угловым коэффициентом k
Вычтя это уравнение из уравнения (3.4), получим уравнение прямой, проходящей через точку М с угловым коэффициентом k
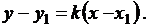 (3.5)
(3.5)
Если прямая проходит через точки М1(х1;у1) и М2(х2;у2), то координаты второй точки можно подставить в уравнение (3.4) 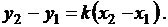 Откуда следует, что
Откуда следует, что 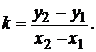 После подстановки найденного k в уравнение (3.5) получим уравнение прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2)
После подстановки найденного k в уравнение (3.5) получим уравнение прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2)
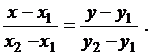 (3.6)
(3.6)
Если прямая линия отсекает на обеих осях отрезки не равные нулю (ни один из коэффициентов общего уравнения (3.3) не равен нулю), то такую прямую можно представить в виде
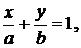 (3.7)
(3.7)
где 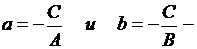 величины отрезков, которые прямая отсекает на координатных осях. Поэтому уравнение (3.7) называют уравнением прямой в отрезках.
величины отрезков, которые прямая отсекает на координатных осях. Поэтому уравнение (3.7) называют уравнением прямой в отрезках.
Взаимное расположение двух прямых
Пусть даны две прямые
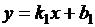 и
и 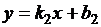 .
.
Угол θ между двумя пересекающимися прямыми (рис. 3.4.) определяется из равенства
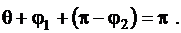
Откуда 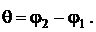
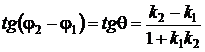 . (3.8)
. (3.8)
Две прямые параллельны, если θ = 0, тогда tg0 = 0, то есть k1 = k2, а b1 ≠ b2. В случае, если b1 = b2, то прямые совпадают.
Две прямые перпендикулярны, если 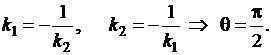
Пример:
Дана прямая линия 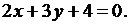 Составить уравнение прямой, проходящей через точку М0(2;1):
Составить уравнение прямой, проходящей через точку М0(2;1):
а) параллельной данной прямой;
б) перпендикулярной данной прямой.
Решение:найдем угловой коэффициент данной прямой
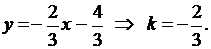 Используя уравнение (3.5) и условие параллельности двух прямых, получим уравнение прямой, параллельной данной и проходящей через точку М0
Используя уравнение (3.5) и условие параллельности двух прямых, получим уравнение прямой, параллельной данной и проходящей через точку М0 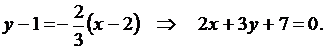
Из условия перпендикулярности двух прямых и уравнения (3.5) получим уравнение прямой, перпендикулярной данной и проходящей через точку М0
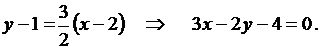
Пример:
Найти координаты вершин треугольника, стороны которого заданы уравнениями: 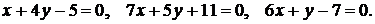
Решение:пусть точки А,В, и С – вершины данного треугольника. Длянахождения их координат следует решить три системы линейных уравнений
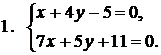 2.
2. 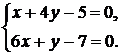 3.
3. 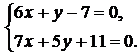
Решим первую систему по правилу Крамера:
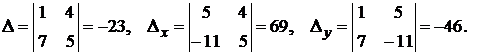
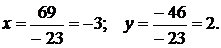
Две другие системы предлагается решить самостоятельно.
Ответ: А(–3;2), В(1;1), С(2;–5).
Пример:
Даны вершины треугольника А(–8;3), В(8;5), С(6;–5). Найти внутренние углы треугольника АВС.
Решение:для определения угла А найдём уравнения прямых АВ и АС по формуле (3.6). Уравнения прямых АВ и АС будут иметь вид, соответственно:
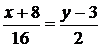 и
и 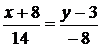 .
.
Угловые коэффициенты этих прямых, соответственно, равны: 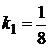 и
и 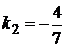 . Тогда, по формуле (3.8), получим
. Тогда, по формуле (3.8), получим
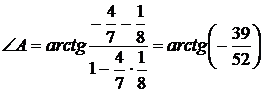 .
.
Два других угла предлагается определить самостоятельно.
Ответ: 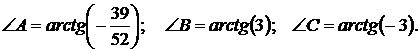
Нормальное уравнение прямой линии.
Из начала координат к прямой линии 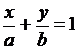 проведём перпендикуляр (рис.3.4). Умножив обе части уравнения (3.7) на длину перпендикуляра р, получим
проведём перпендикуляр (рис.3.4). Умножив обе части уравнения (3.7) на длину перпендикуляра р, получим
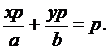
Отношения 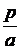 и
и 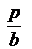 равны
равны 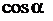 и
и 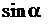 соответственно. И тогда, получим уравнение прямой линии в виде
соответственно. И тогда, получим уравнение прямой линии в виде
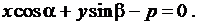 (3.9)
(3.9)
Уравнение (3.9) называется нормальным уравнением прямой.
Найдём связь между общим (3.3) и нормальным (3.9) уравнениями прямой.
Длину перпендикуляра можно выразить через отрезки a и b, рассматривая прямоугольные треугольники на рис. 3.4.
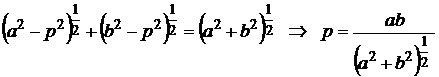
Тогда коэффициенты в уравнении (3.9) будут
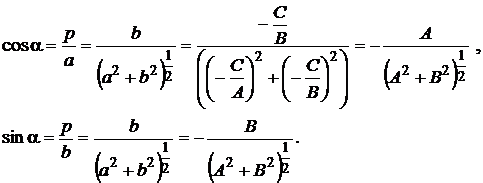
Для того, чтобы общее уравнение прямой 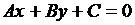 привести к нормальному виду, нужно все члены уравнения умножить на нормирующий множитель
привести к нормальному виду, нужно все члены уравнения умножить на нормирующий множитель
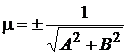 .
.
Знак выбирается противоположным знаку при С в уравнении (3.3).
Уравнение прямой в нормальном виде удобно использовать для определения расстояния d от произвольной точки М(х1;у1) до прямой, подставляя координаты х1 и у1 в уравнение (3.9)
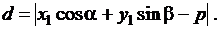
Пример:
Найти расстояние d от точки А(1;2) до прямой 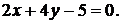
Решение:приведем уравнение прямой к нормальному виду, умножив его на нормирующий множитель 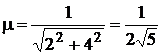 .
.
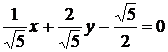 . Отсюда
. Отсюда 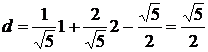 .
.
Кривые второго порядка.
Уравнение
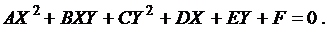 (3.10)
(3.10)
называется общим уравнением кривых второго порядка. Это уравнение с помощью преобразования координат можно привести к каконическому уравнению эллипса, гиперболы, или параболы, или к уравнению двух прямых линий.
Преобразование координат
Преобразованием координат называют переход от системы координат XОY к новой системе хоу.
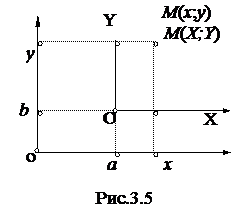
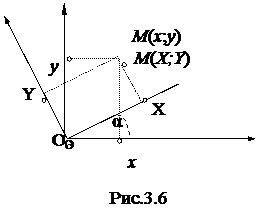 Существует 2 способа преобразования: параллельный перенос осей (рис.3.5) и поворот осей на угол α (рис.3.6).
Существует 2 способа преобразования: параллельный перенос осей (рис.3.5) и поворот осей на угол α (рис.3.6).
 Координаты произвольной точки М изменяются:
Координаты произвольной точки М изменяются:
а) при параллельном переносе осей;
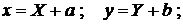 (3.11)
(3.11)
б) при повороте осей на угол α
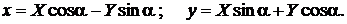 (3.12)
(3.12)
Для упрощения уравнения (3.10) необходимо освободиться от члена с произведением координат, то есть, от ВХY, с помощью поворота осей. Из формул (3.12) находим

и подставляем в (3.10). Слагаемые, содержащие ху, приравняем к нулю 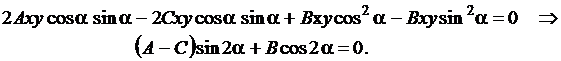
Находим соотношение для определения угла поворота осей