Линейные операторы и их матрицы

Понятие линейного оператора

Пусть V и W– два линейных пространства. Отображение А : V → Wназывается линейным оператором, если

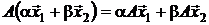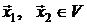, где , α, β ∈ R.

Вектор 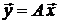называется образом вектора 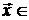V.

Оператор, который каждому вектору 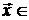V ставит в соответствие нулевой вектор 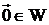, называется нулевым оператором и обозначается О. Таким образом, 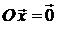, 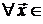V.

Линейный оператор А, для которого 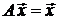, 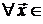V, называется тождественным и обозначается Е.

Оператор А,удовлетворяющий соотношению 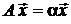, где α ∈ R,называется скалярнымоператором или оператором подобия.

Областью значений линейного оператора А : V → Wназывается множество векторов вида 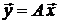, 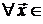V, и обозначается im A(англ. image − образ).

Ядром линейного оператора А называется множество ker А всех 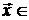V, для которых 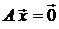(англ. kernel − ядро).

Матрица линейного оператора

Пусть V – линейное пространство с базисом 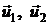, а А – линейный оператор, действующий из в линейное пространство W, базисом которого служат векторы 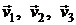. (Для простоты изложения будем рассматривать линейные пространства Vразмерности n =2 и W – m = 3.) Тогда любой вектор 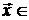V можно представить в виде 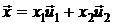. В силу линейности оператора А получим

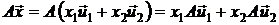(2.19)

Векторы 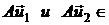W однозначно разлагаются по базису векторов пространства W:

(2.20)

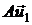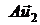где (а₁₁; а₂₁; а₃₁) и (а₁₂; а₂₂; а₃₂) – координаты векторов и соответственно в базисе 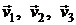. Так как вектор 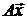тоже принадлежит пространству W, то аналогично

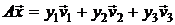, (2.21)

где у₁ и у₂ – координаты вектора 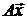в пространстве W. Из формул (2.19), (2.20) и (2.21) получим

,

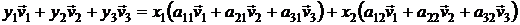откуда, приравняв координаты при соответствующих векторах 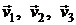, получим систему равенств вида

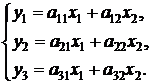(2.22)

Равенства (2.22) позволяют вычислить координаты у₁, у₂, у₃ вектора

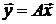
при линейном отображении

А : V → W

через координатых₁, х₂ вектора 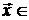V, линейный оператор А имеет вид

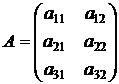. (2.23)

Из равенств (2.22) и (2.23) следует, что при заданных базисах 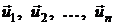в пространстве V и 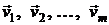в пространстве Wлинейный оператор А : V → Wполностью определяется матрицей

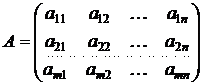, (2.24)

которая называется матрицей линейного оператора А выбранных базисах.

Между множествами матриц и линейных операторов устанавливается взаимно-однозначное соответствие, поэтому линейные операторы и соответствующие им матрицы обозначают одними и теми же буквами, то есть если А – линейный оператор, то А – его матрица.

Таким образом, равенство 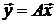в координатной форме имеет вид

. (2.25)

Примеры линейных операторов

Если А : R² → R² или А : R³ → R³ – линейные операторы. действующие в пространстве R² или R³, то их матрицы имеют вид

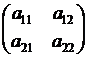или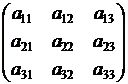

соответственно. Эти операторы переводят векторы из R² в векторы из R² или векторы из R³ в векторы того же пространства R³. Рассмотрим некоторые таких линейных операторов.

Пусть А– оператор подобия, отображающий вектор 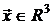в некоторый параллельный ему вектор 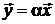. Линейность этого оператора очевидна.

Если 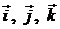– базис пространства R³, то

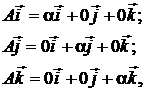
и, значит, матрица этого оператора

.

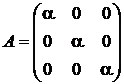При α = 1 получим матрицу Е тождественного оператора, при α = –1 – матрицу – Е оператора, противоположного тождественному, при α = 0 – матрицу нулевого оператора.

Пусть А– оператор поворота векторов плоскости R²вокруг начала координат на угол φ против часовой стрелки. Это преобразование линейно.

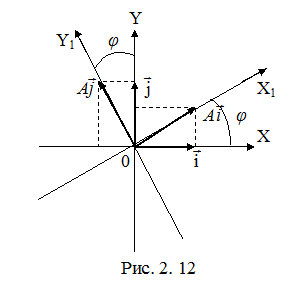Найдем матрицу оператора поворота. Из рис. 2. 12 видно, что

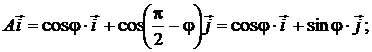
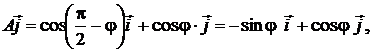так что матрица поворота в базисе 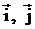имеет вид

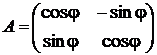. (2.26)

Матрица А, определённая равенством (2.26), называется матрицей перехода от старого базиса к новому (рис. 2.12).

Используя матрицу (2.26), получим формулы преобразования координат вектора при повороте на угол φ. Пусть х₁, х₂ – координаты вектора 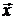, тогда координаты у₁, у₂ вектора 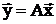при повороте вектора на угол φ определяются из соотношений

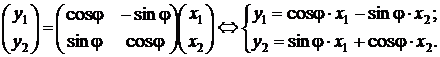
Пример:

Пусть А: R³ → R² – линейный оператор, для которого 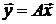, где

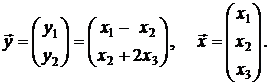
Найти матрицу перехода оператора А.

Решение: согласно условию и равенству (2.24), матрица А имеет две строки и три столбца:

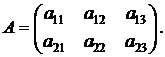
По определению,

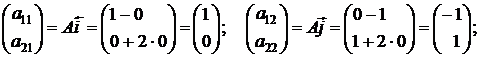
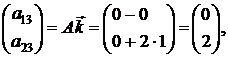
так что

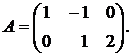
Матрицу А получить проще, если воспользоваться тем, что её строки составлены из коэффициентов разложения координат вектора 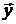по координатам вектора 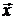, то есть из условия задачи следует, что

у₁ = 1∙ х₁ – 1∙ х₂ + 0 ∙ х₃, откуда а₁₁ = 1, а₁₂ = – 1, а₁₃ = 0;

у₁ = 0 ∙ х₁ + 1∙ х₂ + 2 ∙ х₃, откуда а₂₁ = 0, а₂₂ = 1, а₂₃ = 2.