Условие статической определимости кинематических цепей.

Необходимо помнить, что кинематические цепи, имеющие степень подвижности w=0, в силовом отношении являются статически определенными. Условие статической определимости плоских кинематических цепей записывается в виде: 3n - 2p₅ - p₄ = 0 где n - число подвижных звеньев P₅ и P₄ число кинемат пар 5 и 4 класса, 3 – число уравнений статики, которое можно составить для каждого подвижного звена в плоскости.

Плоская кинематическая цепь может состоять из кинематических пар 5-го класса (вращательных, поступательных) и пар 4-го класса (высших, у которых звенья соприкасаются в точке. Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности.

В поступательной паре (рис .6.1, а) реакции направлены перпендикулярно направляющей. Неизвестных здесь две: величина силы F01 и точка ее приложения (расстояние h). Во вращательной паре равнодействующая сил реакции направлена по нормали к цилиндрической поверхности, т.е. проходит через центр шарнира (рис. 6.1, б). Неизвестными являются : направление реакции (угол β) и величина силы. Таким образом, эта пара также вносит в уравнения кинетостатики две неизвестных. Следовательно, от каждой силы, действующей в любой низшей кинематической паре, в расчетных уравнениях появляются две неизвестные величины.

В высших парах сила взаимодействия между звеньями направлена по общей нормали и приложена в точке касания, т.е. известны и направление и точка приложения силы (рис. 6.1, в), неизвестна лишь ее величина. Поэтому в расчетных уравнениях члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.

В общем виде общ числ неизвестн Nн = 2⋅p5+ p4(6.2)

Число уравнений статики для каждого звена плоского механизма равно 3, значит, общее число уравнений для n подвижных звеньев Nу =3n. (6.3)

Чтобы система была статически определимой, число уравнений Nу должно быть равно числу неизвестных Nн . Приравниваем (6.2) и (6.3), после чего получим: 3n = 2⋅p5+ p4. (56.4)

Если заменить высшие пары низшими, то получим 3n = 2⋅p5. (5.4)

Из этого можно сделать вывод, что группы Ассура являются статически определимыми.

На основании вышеизложенного формулируется общая методика силового анализа: расчет необходимо проводить по структурным группам, начиная с наиболее удаленной от начального звена и заканчивая начальным звеном (механизмом I класса). Таким образом, силовой расчет проводится в порядке, обратном кинематическому.

19Силовой расчет рычажных механизмов методом планов

Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т.е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению.

При графоаналитическом решении используется метод плана сил. Механизм расчленяется на структурные группы Ассура и начальные звенья. Расчет ведется, начиная с последней структурной группы и заканчивается расчетом входного звена.

При расчете структурных групп к ним прикладываются все действующие силы, включая силы инерции и реакции отброшенных связей. Каждая из неизвестных реакций, при необходимости, может быть разложена на две составляющие по выбранным направлениям, например, вдоль оси звена (нормальная Fn) и перпендикулярно оси (тангенциальная Ft). При равенстве числа уравнений статики числу неизвестных реакций их можно определить аналитически и графически, построив многоугольник (план) сил. Неизвестные определятся из условия замкнутости векторной суммы сил. Графическое определение реакций в кинематических парах плоских механизмов с помощью планов сил применяется не только вследствие наглядности, но и потому, что внешние силы, действующие на звенья механизма, обычно известны лишь приближённо, и точность простейших графических построений оказывается вполне достаточной

Виды трения

Трение – это сопротивление, возникающее при относительном перемещении двух соприкасающихся тел в плоскости их контакта. Сила трения – это сила сопротивления, направленная противоположно сдвигающему усилию.

На схеме (рис. 37) представлена классификация видов трения по основополагающим признакам.

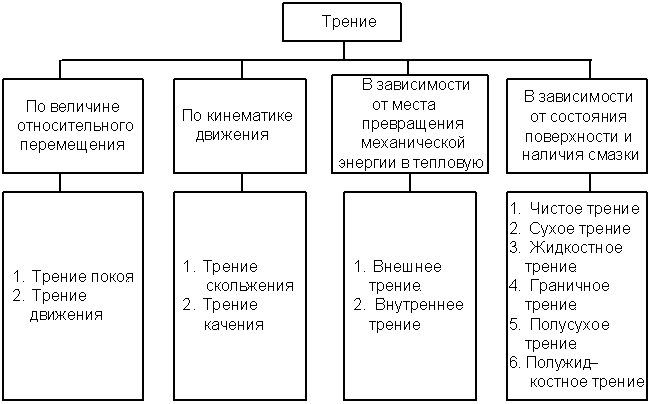
Трение скольжения – это сопротивление, возникающее при перемещении одной и той же поверхности одного тела по поверхности другого тела.

Основными положениями закона сухого трения скольжения являются:

1. Сила трения скольжения на плоскости прямо пропорциональна нормальному давлению в определенном диапазоне скоростей и и нагрузок.

2. Направление силы трения скольжения противоположно относительной скорости трущихся тел.

3. Точное положение точки приложения силы трения скольжения неизвестно.

4. Трение зависит от материала и состояния трущихся поверхностей.

5. С увеличением скорости движения сила трения в большинстве случаев уменьшается, приближаясь к некоторому постоянному значению.

6. С возрастанием удельного давления сила трения в большинстве случаев увеличивается.