Вычисление определителей высших порядков
Определитель
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка 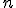 , нужно уже знать, что такое определитель матрицы порядка
, нужно уже знать, что такое определитель матрицы порядка 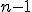 . Отметим также, что определитель существует только у квадратных матриц.
. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы 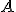 будем обозначать
будем обозначать  или det
или det 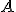 .
.
Определение 1. Определителем квадратной матрицы 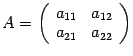 второго порядка называется число
второго порядка называется число 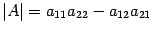 .
.
Определителем 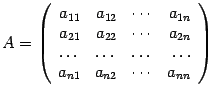 квадратной матрицы порядка
квадратной матрицы порядка 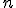 ,
, 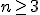 , называется число
, называется число 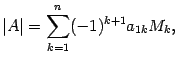
где 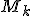 - определитель матрицы порядка
- определитель матрицы порядка 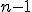 , полученной из матрицы
, полученной из матрицы 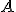 вычеркиванием первой строки и столбца с номером
вычеркиванием первой строки и столбца с номером 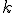 .
.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка: 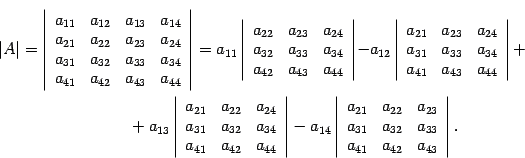
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det 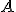 .
.
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Утверждение 1. При транспонировании матрицы определитель не меняется, то есть 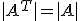 .
.
Утверждение 2. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть 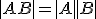 .
.
Утверждение 3. Если в матрице 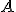 поменять местами две строки, то ее определитель сменит знак.
поменять местами две строки, то ее определитель сменит знак.
Утверждение 4. Если матрица 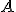 имеет две одинаковые строки, то ее определитель равен нулю.
имеет две одинаковые строки, то ее определитель равен нулю.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Утверждение 5. Если строку матрицы умножить на число 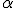 , то ее определитель умножится на это число.
, то ее определитель умножится на это число.
Утверждение 6. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Утверждение 7. Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Утверждение 8. Пусть в матрице 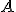 i-ая строка имеет вид
i-ая строка имеет вид 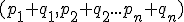 . Тогда
. Тогда 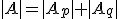 , где матрица
, где матрица 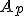 получается из матрицы
получается из матрицы 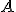 заменой i-ой строки на строку
заменой i-ой строки на строку 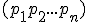 , а матрица
, а матрица 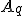 - заменой i-ой строки на строку
- заменой i-ой строки на строку 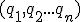 .
.
Утверждение 9. Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Утверждение 10. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Определение 2. Алгебраическим дополнением к элементу 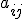 матрицы
матрицы 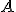 называется число, равное
называется число, равное 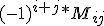 , где
, где 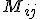 - определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца. Алгебраическое дополнение к элементу
- определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца. Алгебраическое дополнение к элементу 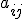 матрицы
матрицы 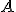 обозначается
обозначается 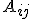 .
.
Пример. Пусть 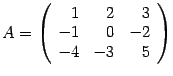 . Тогда
. Тогда 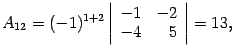
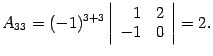
Замечание. Используя алгебраические дополнения, определение 1 определителя можно записать так: