Структурные схемы надежности (ССН). Способы соединения элементов в ССН
РОСЖЕЛДОР
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(ФГБОУ ВПО РГУПС)
А.И. Кирюнин
РАСЧЕТ НАДЁЖДНОСТИ
СИСТЕМ ОБЕСПЕЧЕНИЯ ДВИЖЕНИЯ ПОЕЗДОВ
Методические указания
к лабораторным работам по дисциплине:
«Основы теории надежности»
Ростов–на–Дону
УДК 656.256
Кирюнин А.И.
Расчет надежности систем обеспечения безопасности движения поездов: Методические указания к лабораторным работам по дисциплине: «Основы теории надежности». – Ростов н/Д: Рост. гос. ун-т путей сообщения, 2013. – 00 с.
Излагаются основные сведения теории надежности, приведены примеры решения задач по основным разделам теории. Приведены цели, порядок выполнения лабораторных работ и оформления отчётов, перечни контрольных вопросов.
Методические указания написаны в соответствии с рабочей учебной программой по дисциплине: «Основы теории надежности» и предназначены для студентов специальности 190901 «Системы обеспечения движения поездов».
Одобрены к изданию кафедрой: «Автоматика и телемеханика на железнодорожном транспорте» ФГБОУ ВПО РГУПС.
Табл. 0. Ил. 0. Библиогр.: 0 назв.
Рецензенты:
ã Ростовский государственный университет
 путей сообщения, 2013
путей сообщения, 2013
ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 1
ТЕМА ЗАНЯТИЯ: ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СИСТЕМ ПО РЕЗУЛЬТАТАМ ЭКСПЛУАТАЦИИ
1. ЦЕЛЬ ЗАНЯТИЯ
1.1. Получить и закрепить необходимые теоретические сведения по количественным характеристикам (показателям) надежности систем.
1.2. Получить практические навыки в решении задач по вычислению количественных характеристик (показателей) надежности систем, построении их графиков с использование ЭВМ.
2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
К числу количественных показателей надежности невосстанавливаемых систем относятся:
1. Вероятность безотказной работы за время 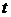
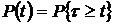 , где
, где 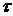 –наработка до отказа;
–наработка до отказа; 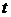 – требуемое время безотказной работы (или время, для которого определяется
– требуемое время безотказной работы (или время, для которого определяется 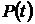 ). Статистическое (приближенное) значение этой вероятности, определяемое по результатам опытных испытаний, равно
). Статистическое (приближенное) значение этой вероятности, определяемое по результатам опытных испытаний, равно
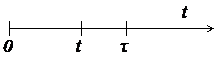
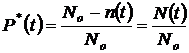
 , (1.1)
, (1.1)
где 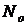 – число однотипных объектов, поставленных на испытание;
– число однотипных объектов, поставленных на испытание;
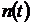 – число отказавших объектов за время испытаний
– число отказавших объектов за время испытаний 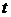 (за интервал времени (0, t));
(за интервал времени (0, t));
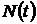 – число не отказавших объектов за время t,
– число не отказавших объектов за время t, 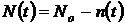 .
.
Далее везде знак * будет обозначать статистическое значение соответствующих показателей надежности.
2. Вероятность отказа объекта за время 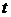
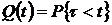 .
.
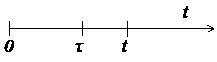
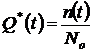 , (1.2)
, (1.2)
причем:
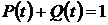 и
и 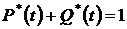 . (1.3)
. (1.3)
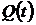 – является функцией распределения случайной величины
– является функцией распределения случайной величины 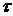 (интегральным законом распределения случайной величины
(интегральным законом распределения случайной величины 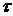 или интегральным законом распределения отказов).
или интегральным законом распределения отказов).
3. Плотность вероятности отказов 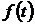 (дифференциальная плотность (закон) распределения времени наработки до отказа
(дифференциальная плотность (закон) распределения времени наработки до отказа 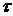 , дифференциальная функция распределения случайной величины
, дифференциальная функция распределения случайной величины 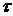 )
)
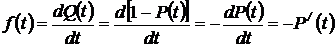 . (1.4)
. (1.4)
Из (1.4) имеем:
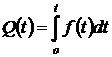 , (1.5)
, (1.5)
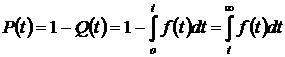 , (1.6)
, (1.6)
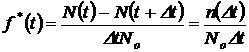 1/ч, (1.7)
1/ч, (1.7)
где 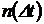 – число отказавших объектов на интервале времени
– число отказавших объектов на интервале времени 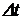 : от t до
: от t до 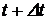 .
.
Экспоненциальный закон распределения времени наработки до отказа 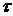 (когда
(когда 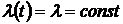 ) определяется формулой
) определяется формулой
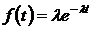 . (1.8)
. (1.8)
4. Интенсивность отказов:
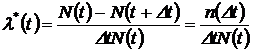 1/ч, (1.9)
1/ч, (1.9)
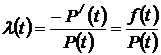 , (1.10)
, (1.10)
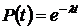 , (1.11)
, (1.11)
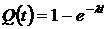 , (1.12)
, (1.12)
5. Средняя наработка до отказа 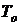 .
.
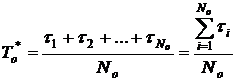 , ч (1.13)
, ч (1.13)
где 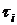 – время наработки до отказа
– время наработки до отказа 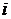 –го образца
–го образца 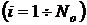 .
.
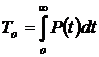 . (1.14)
. (1.14)
ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ
В лабораторной работе используются персональные компьютеры.
ДОМАШНЕЕ ЗАДАНИЕ
Уяснить цель занятия и изучить теоретические сведения, изложенные выше в разделе 2.
ЛАБОРАТОРНОЕ ЗАДАНИЕ
Задачи № 1 и № 2 студенты решают вручную, т.е. определяют значения количественных показателей надежности по формулам, приведенным в разделе 2.
Задачи № 3 и № 4 студенты решают с использованием компьютерной программы Excel для своего варианта (вариант определяется из номера зачетной книжки студента).
Задача № 1. На испытание поставлено 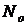 = 2000 однотипных изделий. За время
= 2000 однотипных изделий. За время 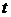 = 4000 часов отказало
= 4000 часов отказало 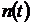 = 100 изделий, а за последующие
= 100 изделий, а за последующие 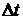 = 100 часов отказало еще
= 100 часов отказало еще 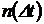 = 10 изделий (см. рис 1.1). Определить статистические показатели надежности:
= 10 изделий (см. рис 1.1). Определить статистические показатели надежности: 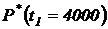 ,
, 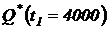 ;
; 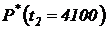 ;
; 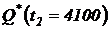 ;
; 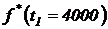 ;
; 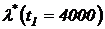 .
.
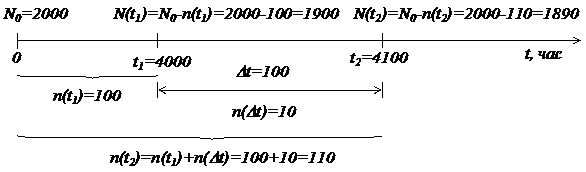 | |||
|
Решение
1. По формулам (1.1) и (1.2) определяем вероятности безотказной работы 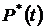 и отказа
и отказа 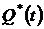 за время испытаний
за время испытаний 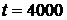 час:
час:
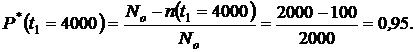
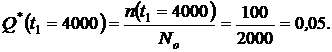
или из формулы (1.3):
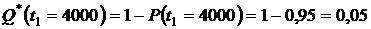 .
.
2. Определяем 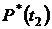 и
и 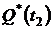 за время испытаний
за время испытаний 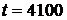 :
:
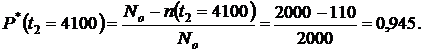
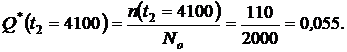
или из формулы (1.3):
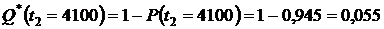 .
.
3. Определяем 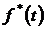 за время
за время 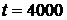 час по формуле (1.7):
час по формуле (1.7):
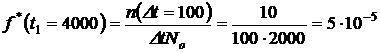 1/ч.
1/ч.
4. Определяем 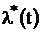 за время
за время 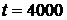 по формуле (1.9):
по формуле (1.9):
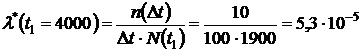 1/ч.
1/ч.
Задача № 2. Пусть время наработки до отказа 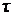 системы обеспечения безопасности движения поездов подчинено экспоненциальному закону
системы обеспечения безопасности движения поездов подчинено экспоненциальному закону 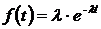 с параметром
с параметром 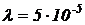 1/ч требуется вычислить показатели надежности
1/ч требуется вычислить показатели надежности 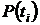 ,
, 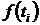
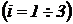 ,
, 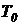 для следующих значений времени:
для следующих значений времени: 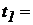 250 ч,
250 ч, 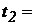 500 ч,
500 ч, 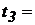 1000 ч.
1000 ч.
Решение
1. Определяем вероятности безотказной работы системы 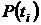 :
:
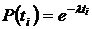
Примечание
Разложение в ряд Тейлора:
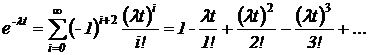
Если 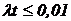 , то
, то 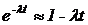 .
.
Если 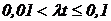 , то
, то 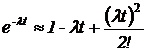 .
.
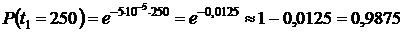 ,
,
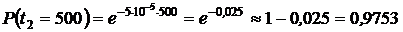 ,
,
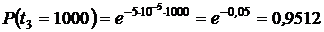 .
.
Выводы:
1. С увеличением времени 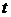 вероятность безотказной работы
вероятность безотказной работы 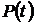 уменьшается.
уменьшается.
2. При 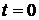 ,
, 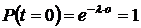 .
.
3. При 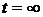 ,
, 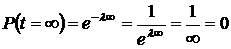 .
.
2. Вычисляем 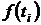 :
:
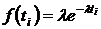 ,
,
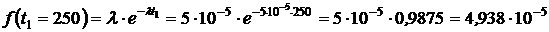 1/ч,
1/ч,
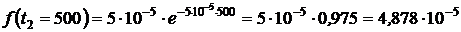 1/ч,
1/ч,
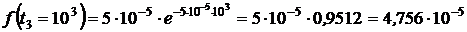 1/ч.
1/ч.
Вывод. С увеличением времени 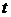 величина
величина 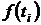 уменьшается.
уменьшается.
3. Вычисляем 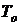 :
:
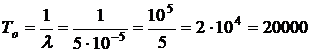 ч.
ч.
Задача № 3. В дистанции запущена в эксплуатацию система обеспечения безопасности движения поездов, содержащая 1600 ( 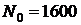 ) однотипных элементов(например, резисторов). Возникающие отказы элементов фиксировались через каждые 100 ч работы (
) однотипных элементов(например, резисторов). Возникающие отказы элементов фиксировались через каждые 100 ч работы ( 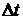 = 100 ч). Данные об отказах приведены в таблице 1.1. При этом к величине
= 100 ч). Данные об отказах приведены в таблице 1.1. При этом к величине 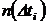 студент прибавляет последнюю цифру номера своей зачетной книжки
студент прибавляет последнюю цифру номера своей зачетной книжки 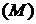 (цифра «0» соответствует
(цифра «0» соответствует 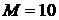 ).
).
Необходимо определить статистические показатели надежности для значений времени 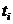 ,
, 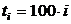 ,
, 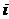 =1
=1 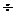 16 для показателей
16 для показателей 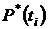 и
и 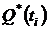 и
и 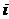 =1
=1 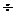 15 для
15 для 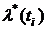 и
и 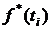 :
:
1) вероятность безотказной работы 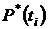 ;
;
2) вероятность отказа 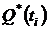 ;
;
3) интенсивность отказов 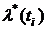 ;
;
4) плотность распределения отказов 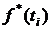 ;
;
5) построить графики указанных характеристик и сделать выводы об их изменениях с увеличением времени 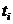 .
.
Таблица 1.1
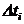 , ч, , ч, 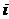 =1 =1 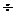 16 16 | 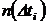 | 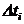 , ч , ч | 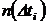 |
| 0 – 100 | 45 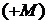 | 800 – 900 | 16 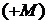 |
| 100 – 200 | 40 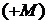 | 900 – 1000 | 16 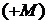 |
| 200 – 300 | 35 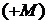 | 1000 – 1100 | 15 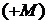 |
| 300 – 400 | 32 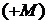 | 1100 – 1200 | 14 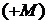 |
| 400 – 500 | 28 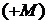 | 1200 – 1300 | 15 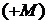 |
| 500 – 600 | 25 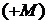 | 1300 – 1400 | 13 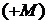 |
| 600 – 700 | 20 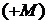 | 1400 – 1500 | 14 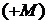 |
| 700 – 800 | 17 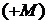 | 1500 – 1600 | 13 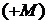 |
Результаты расчетов представить в виде таблицы 1.2.
Задачу необходимо решить (вычислить необходимые значения и построить графики) при помощи компьютерной программы Excel (см. приложение А).
Таблица 1.2
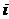 | 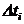 | 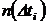 | 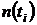 | 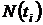 | 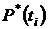 | 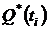 | 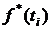 | 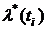 |
| 0 – 100 | ||||||||
| 100 – 200 | ||||||||
| … | … | … | ||||||
| 1500 – 1600 |
Задача № 4. Определить количественные показатели (характеристики) надежности микросхемы, работающей в составе системы обеспечения безопасности движения поездов: 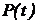 ,
, 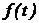 и
и 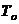 , при условии, что время работы микросхемы до отказа подчиняется экспоненциальному закону распределения. Показатели надежности
, при условии, что время работы микросхемы до отказа подчиняется экспоненциальному закону распределения. Показатели надежности 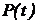 и
и 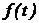 определить на интервале от 0 до 1000 часов с шагом в 100 часов. Построить графики функций
определить на интервале от 0 до 1000 часов с шагом в 100 часов. Построить графики функций 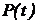 ,
, 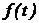 и сделать выводы об их изменении с течением времени
и сделать выводы об их изменении с течением времени 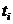 .
.
Номер варианта задачи для каждого студента определяется заданием значения интенсивности отказов по формуле 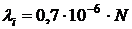 , где
, где 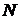 – предпоследняя цифра номера зачетной книжки студента (цифра «0» соответствует
– предпоследняя цифра номера зачетной книжки студента (цифра «0» соответствует 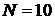 ).
).
Результаты расчетов представить в виде таблицы 1.3.
Задачу необходимо решить (вычислить необходимые значения и построить графики) при помощи компьютерной программы Excel.
Таблица 1.3
 | 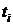 , час , час | 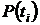 | 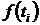 , 1/час , 1/час |
| … | … | ||
СОДЕРЖАНИЕ ОТЧЕТА
1. Формулы для расчета количественных показателей надежности.
2. Описание хода решения задачи:
- задачи №3 – для первых трех интервалов времени ( 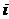 =1
=1 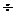 3) (по аналогии с ходом решения, приведенного для задачи № 1);
3) (по аналогии с ходом решения, приведенного для задачи № 1);
- задачи № 4 – для первых трех моментов времени ( 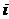 =0
=0 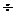 2) (по аналогии с ходом решения, приведенного для задачи № 2).
2) (по аналогии с ходом решения, приведенного для задачи № 2).
3. Распечатка таблицы 1.2 с результатами решения задачи № 3 и таблицы 1.3 с результатами решения задачи № 4.
4. Распечатка графиков функций для задачи № 3 и задачи № 4.
5. Выводы по полученным результатам.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основные понятия теории надежности: надежность, безотказность, ремонтопригодность, долговечность, сохраняемость, отказ, виды отказов.
2. Количественные показатели надежности (безотказности) невосстанавливаемых систем:
– вероятности безотказной работы 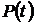 ,
, 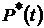 и отказа
и отказа 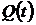
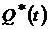 . Графики функций
. Графики функций 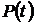 и
и 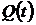 ;
;
– плотность вероятности отказов 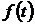 ,
, 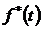 . Связь вероятностей
. Связь вероятностей 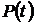 и
и 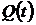 с
с 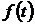 . Связь
. Связь 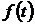 с
с 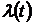 ;
;
– интенсивность отказов 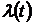 ,
, 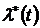 . График функции
. График функции 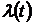 . Связь
. Связь 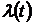 с
с 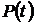 ,
, 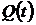 и
и 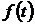 ;
;
– средняя наработка до отказа 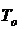 ,
, 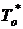 . Связь показателя
. Связь показателя 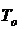 с вероятностью безотказной работы
с вероятностью безотказной работы 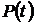 .
.
Записать и пояснить формулы для данных показателей безотказности и пояснить их физический смысл.
3. Вычисление количественных показателей (характеристик) надежности невосстанавливаемых систем.
ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 2
ТЕМА ЗАНЯТИЯ: ИССЛЕДОВАНИЕ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ С РАЗЛИЧНЫМИ СПОСОБАМИ РЕЗЕРВИРОВАНИЯ
1. ЦЕЛЬ ЗАНЯТИЯ
1.1. Получить и закрепить необходимые теоретические знания по способам структурного резервирования невосстанавливаемых систем и методикам расчета надежности таких систем.
1.2. Получить практические навыки в решении задач по расчету надежности систем с различными способами структурного резервирования с использование ЭВМ.
.
2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ
В лабораторной работе используются персональные компьютеры.
ДОМАШНЕЕ ЗАДАНИЕ
Уяснить цель занятия и изучить теоретические сведения, изложенные выше в разделе 2.
ЛАБОРАТОРНОЕ ЗАДАНИЕ
Задачи № 1 и № 2 студенты решают вручную, т.е. определяют значения количественных показателей надежности по формулам, приведенным в разделе 2.
Задачу № 3 студенты решают вручную для своего варианта (вариант определяется из номера зачетной книжки студента) с последующей проверкой полученных результатов в компьютерной программе.
Задача № 1.Задана структурная схема надежности резервированного устройства (рис 2.4). Показатели надежности устройства распределены по экспоненциальному закону распределения. Интенсивности отказов элементов имеют следующие значения:
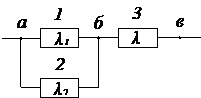 |
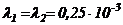 1/ч,
1/ч,
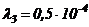 1/ч.
1/ч.
|
Определить вероятность безотказной работы устройства 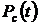 для
для 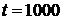 часов и среднюю наработку до отказа
часов и среднюю наработку до отказа 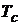 устройства.
устройства.
Решение
1. Определяем 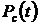
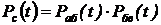 ,
,
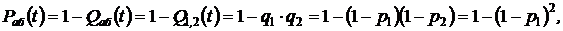
где 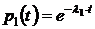 ,
, 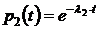 и
и 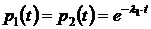 .
.
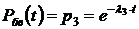 .
.
Тогда:
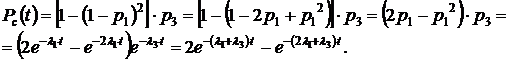
Подставляем числовые значения из условия задачи:
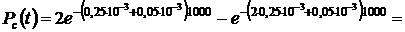
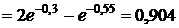 .
.
2. Определяем 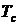 :
:
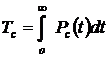 ,
,
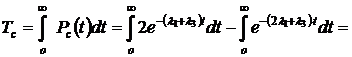
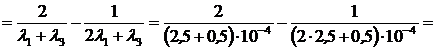
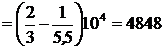 ч.
ч.
Задача № 2.Имеется две структурные схемы надежности (рис. 2.5 а, б):
- с постоянным общим резервированием (рис. 2.5 а);
- с постоянным раздельным резервированием (рис. 2.5 б)
 | |||||||||
 | |||||||||
| |||||||||
| |||||||||
| |||||||||
Все элементы 1 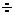 4 схем «а» и «б» является равнонадежными, т.е.
4 схем «а» и «б» является равнонадежными, т.е. 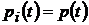 , где
, где 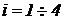 .
.
Определить:
1. Вероятности безотказной работы (ВБР) схем «а» и «б»: 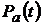 и
и 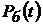 .
.
2. Какая из схем лучше по надежности, т.е. насколько ВБР лучшей схемы больше ВБР худшей схемы?
Решение
1. Определяем ВБР схемы «а»:
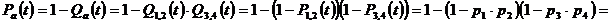
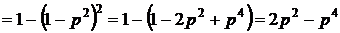 .
.
2. Определяем ВБР схемы «б»:
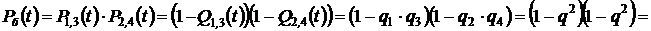
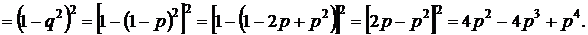
3. Определяем, какая из схем лучше:
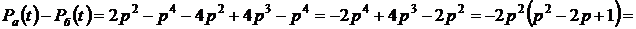
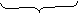
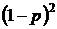
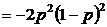 ,
,
|
т.к. 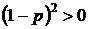 , то .
, то .
Вывод. Лучшей схемой по критерию ВБР является схема «б».
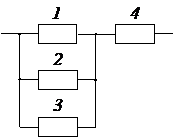
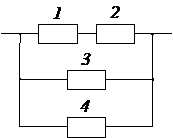
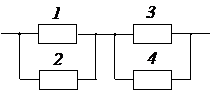
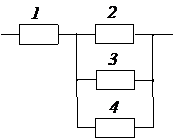
Задача № 3.Задана структурная схема надежности резервированного устройства (рис. 2.6). Показатели надежности устройства распределены по экспоненциальному закону распределения. Исходные данные для расчета приведены в таблице 2.1. Номер схемы и вариант определяется последней цифрой номера зачетной книжки студента (цифра «0» соответствует схеме и варианту 10).
 | |||||||||||||||||||||||||||||||||||||
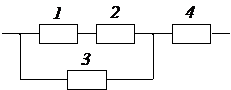 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||
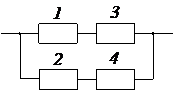 | |||||||||||||||||||||||||||||||||||||
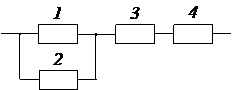 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
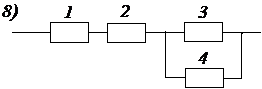 | |||||||||||||||||||||||||||||||||||||
| 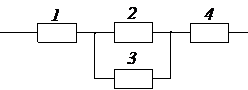 | ||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
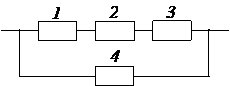 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
Таблица 2.1
| Вариант | 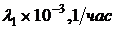 | 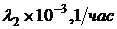 | 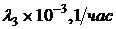 | 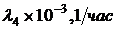 | 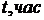 |
| 0,1 | 0,2 | 0,3 | 0,4 | ||
| 0,2 | 0,3 | 0,4 | 0,1 | ||
| 0,3 | 0,4 | 0,1 | 0,2 | ||
| 0,4 | 0,1 | 0,2 | 0,3 | ||
| 0,1 | 0,4 | 0,2 | 0,3 | ||
| 0,2 | 0,1 | 0,3 | 0,4 | ||
| 0,3 | 0,2 | 0,4 | 0,1 | ||
| 0,4 | 0,3 | 0,1 | 0,2 | ||
| 0,1 | 0,3 | 0,4 | 0,2 | ||
| 0,2 | 0,4 | 0,3 | 0,1 |
Определить:
1. Вероятность безотказной работы устройства 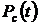 .
.
2. Среднюю наработку до отказа 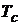 устройства.
устройства.
3. Какая из структурных схем рис. 2.6 является более надежной по критерию ВБР.
Для ответа на вопросы № 1 и № 2 задачу необходимо решить вручную, воспользовавшись формулами, приведенными в разделе 2. Полученные результаты необходимо сравнить с результатами расчетов предложенной компьютерной программы (описание порядка работы с компьютерной программой приведено ниже). В случае расхождения полученных результатов, постарайтесь самостоятельно определить ошибку в своих расчетах.
Ответа на вопрос № 3 задачи можно получить, решив задачу, одним из следующих способов:
1. Попарно сравнить ВБР предложенных ССН устройства, по полученным выражениям 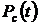 для каждой из схем (задача решается в общем виде (без конкретных числовых значений) по аналогии с задачей №2).
для каждой из схем (задача решается в общем виде (без конкретных числовых значений) по аналогии с задачей №2).
2. Сравнить числовые значения ВБР предложенных ССН устройства, по полученным выражениям 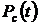 для каждой из схем, считая, что во всех схемах элементы с одинаковыми порядковыми номерами равнонадёжны. Например, для всех схем можно принять следующие значения:
для каждой из схем, считая, что во всех схемах элементы с одинаковыми порядковыми номерами равнонадёжны. Например, для всех схем можно принять следующие значения: 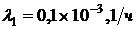 ,
, 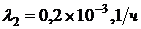 ,
, 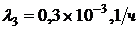 ,
, 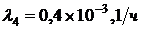 для
для 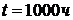 .
.
Полученный результат необходимо сравнить с результатом расчетов компьютерной программы.
 Ярлык компьютерной программы «Расчет надежности невосстанавливаемых резервированных систем» размещается на рабочем столе персонального компьютера.
Ярлык компьютерной программы «Расчет надежности невосстанавливаемых резервированных систем» размещается на рабочем столе персонального компьютера.
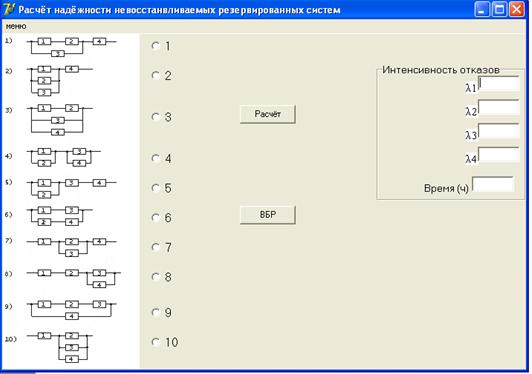
После запуска программы на мониторе будет выведено следующее окно (см. рис. 2.7)
|
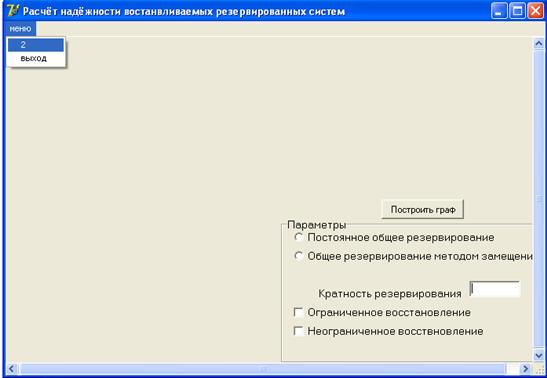
В случае, если на мониторе отображается другое окно программы, необходимо перейти к окну, показанному на рис. 2.7. Для этого на панели инструментов окна программы необходимо выбрать «Меню». В открывшемся окне из списка выбрать «2» (рис. 2.8). Программа перейдет к необходимому окну.
|
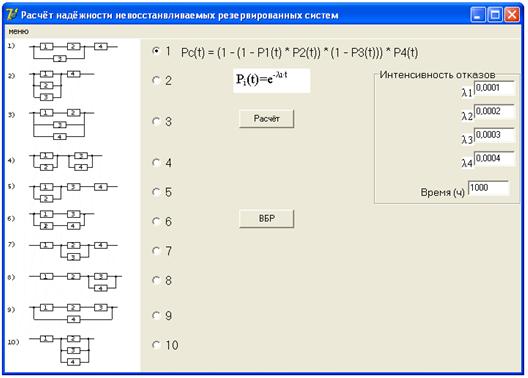
В окне программы «Расчет надежности невосстанавливаемых резервированных систем» (см. рис 2.7) необходимо выбрать (в соответствии со своим вариантом) структурную схему надежности устройства. Для этого необходимо отметить номер схемы (см. рис 2.9).
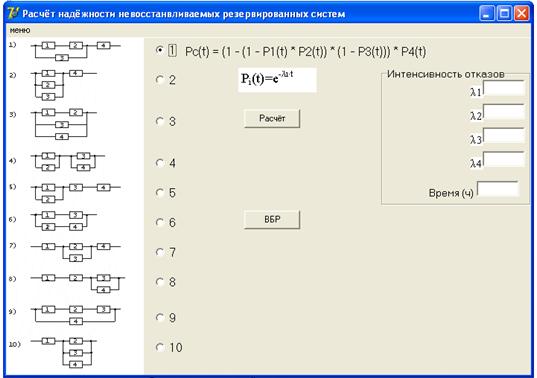
|
В окне программы отобразится выражение для вероятности безотказной работы 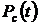 для выбранной схемы. Ниже выражения
для выбранной схемы. Ниже выражения 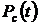 указывается, закон по которому распределены вероятности безотказной работы элементов схемы (
указывается, закон по которому распределены вероятности безотказной работы элементов схемы ( 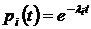 ) – экспоненциальный (не меняется).
) – экспоненциальный (не меняется).
Для определения численных значений вероятности безотказной работы 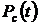 и средней наработки до отказа
и средней наработки до отказа 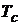 выбранной схемы устройства в правой части окна программы в поле «Интенсивность отказов/Время (ч)» (см. рис. 2.10) необходимо ввести соответствующие значения исходных данных для своего варианта (см. табл. 2.1). Внимание! Значение интенсивности отказа вводится в виде конечной десятичной дроби (без указания мантиссы и порядка числа): 0,0001 (вместо 0,1×10-3).
выбранной схемы устройства в правой части окна программы в поле «Интенсивность отказов/Время (ч)» (см. рис. 2.10) необходимо ввести соответствующие значения исходных данных для своего варианта (см. табл. 2.1). Внимание! Значение интенсивности отказа вводится в виде конечной десятичной дроби (без указания мантиссы и порядка числа): 0,0001 (вместо 0,1×10-3).
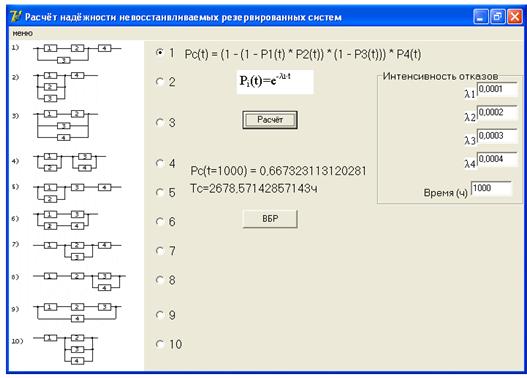
После нажатия кнопки «Расчет» в окне программы отобразятся числовые значения вероятности безотказной работы 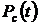 и средней наработки до отказа
и средней наработки до отказа 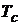 выбранной схемы устройства (см. рис. 2.11).
выбранной схемы устройства (см. рис. 2.11).
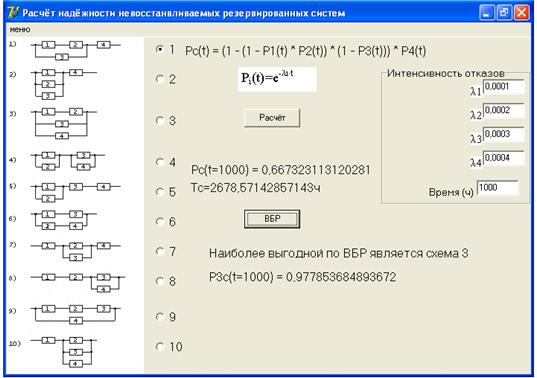
При нажатии кнопки «ВБР» программа определяет наиболее надежную (по критерию «вероятность безотказной работы») схему устройства среди всех имеющихся десяти вариантов для заданных исходных данных. Сообщение о наиболее надежной схеме, с указанием числового значения  для этой схемы, выводится в окне программы (см. 2.12).
для этой схемы, выводится в окне программы (см. 2.12).
|
|
|
При необходимости расчеты показателей надежности могут быть повторены для других исходных данных и другой схемы устройства по изложенной методике.
После окончания работы для выхода из программы необходимо на панели инструментов окна программы выбрать «Меню». В открывшемся окне из списка выбрать «Выход» (рис. 2.13). Программа будет закрыта.

|
СОДЕРЖАНИЕ ОТЧЕТА
1. Формулы для расчета надежности нерезервированных и резервированных невосстанавливаемых систем.
2. Решение задачи № 3 для заданных исходных данных (в соответствии с вариантом).
3. Распечатка (Print Screen) компьютерной программы с результатами расчета (в соответствии с вариантом).
4. Выводы по полученным результатам.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Понятие о структурной схеме надежности (ССН).
2. Способы соединений элементов в ССН. Определение вероятности безотказной работы и средней наработки до отказа схем при:
– последовательном соединении элементов;
– параллельном соединении элементов;
– последовательно–параллельном (смешанном) соединении элементов.
3. Понятие резервирования. Виды резервирования. Способы структурного резервирования.
4. Расчет надежности невосстанавливаемых систем с постоянным общим резервированием.
5. Расчет надежности невосстанавливаемых систем с раздельным (поэлементным) резервированием.
6. Расчет надежности невосстанавливаемых систем с общим резервированием способом замещения.
ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 3
ТЕМА ЗАНЯТИЯ: ИССЛЕДОВАНИЕ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
РЕЗЕРВИРОВАННЫХ СИСТЕМ
1. ЦЕЛЬ ЗАНЯТИЯ
1.1. Получить и закрепить необходимые теоретические знания по расчету надежности восстанавливаемых резервированных систем.
1.2. Получить прак
