Восстановление с разделением бригады
Граф состояний для этого случая (рис. 15.6) аналогичен графу состояний системы с общим однократным облегченным резервированием и с разделением бригады (рис. 15.3) и, как в предыдущем случае, отличается отсутствием перехода из состояния  в состояние
в состояние  .
.
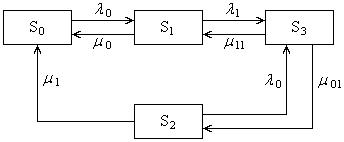
Рис. 15.6. Граф состояний системы с общим однократным ненагруженным резервированием с разделением бригады при восстановлении
Для установившегося режима работы системы с общим однократным ненагруженным резервированием и вариантом восстановления с разделением бригады система уравнений академика Колмогорова имеет вид:
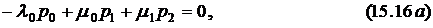
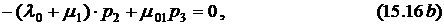
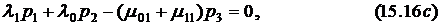

Решая систему уравнений (15.16), получим
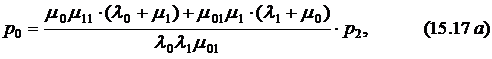
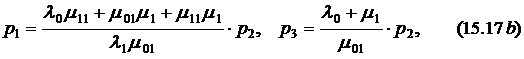
где 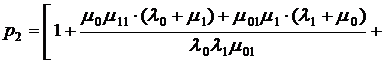
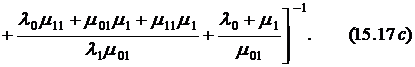
Вероятность безотказной работы системы с общим однократным ненагруженным резервированием и вариантом восстановления с разделением бригады можно рассчитать по формуле

Если резервное устройство аналогично основному, то выполняются условия  ,
, 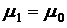 и
и 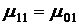 , а граф состояний при этом не изменится.
, а граф состояний при этом не изменится.
Лекция 16. «Комплексы массового обслуживания»
План лекции:
16.1. Основные определения
КМО с отказами
КМО с ожиданием
КМО с ошибками
Замкнутые КМО
16.1. Основные определения
В практике эксплуатации однотипных радиоэлектронных устройств (РЭУ) весьма часто возникают задачи обеспечения требуемой надёжности их совокупности путём организации ремонта отказавших. При этом под термином "требуемая надёжность" понимают относительное количество исправных устройств, которых в любой момент времени должно быть не менее заданного значения.
К таким задачам относят, например, поддержание в исправном состоянии бытовой радиоаппаратуры, радиоизмерительных приборов на предприятиях, в КБ, НИИ, на автомобильном, морском и железнодорожном транспорте, радионавигационной и связной аппаратуры в авиации, в вооружённых силах и т.д.
Резервирование обеспечивает получение требуемой надёжности для отдельного устройства в течение заданного интервала времени. А для обеспечения заданной надёжности совокупности устройств в течение длительного времени необходимо создание ремонтных комплексов типа телеателье, мастерских, заводов, бригад и т.д. Такие системы массового обслуживания называюткомплексами массового обслуживания (КМО).
КМО представляют собой, по существу, одноканальные или многоканальные СМО с различной дисциплиной обслуживания поступающих в неё заявок.
Принято считать совокупность из 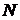 однотипных РЭУ достаточно большой, так что общая интенсивность отказов
однотипных РЭУ достаточно большой, так что общая интенсивность отказов 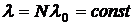 не зависит от числа отказавших устройств. Здесь
не зависит от числа отказавших устройств. Здесь 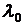 – интенсивность отказов отдельного устройства.
– интенсивность отказов отдельного устройства.
Обозначим через 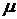 интенсивность восстановления устройства одним каналом КМО.
интенсивность восстановления устройства одним каналом КМО.
Разновидностями КМО являются:
1) СМО с отказами,
2) СМО с ожиданием,
3) СМО с ошибками,
4) замкнутые СМО и некоторые другие.
КМО с отказами
Рассмотрим КМО с отказами, к которым можно отнести, например, городскую телефонную сеть.
Пусть  – число каналов СМО. Обозначим в самом общем случае интенсивность перехода из состояния
– число каналов СМО. Обозначим в самом общем случае интенсивность перехода из состояния 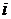 в состояние
в состояние 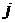 через
через 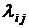 (рис. 16.1).
(рис. 16.1).

Рис. 16.1. СМО с отказами (схема "гибели-размножения")
Случайный процесс, протекающий в системе массового обслуживания, называют марковским или "процессом без последействия", если для каждого момента времени вероятность любого состояния системы в будущем зависит только от её состояния в настоящем и не зависит от того, когда и каким образом система пришла в это состояние, то есть как развивался процесс в прошлом.
Случайную последовательность событий называют марковской цепью, если для каждого шага вероятность перехода из любого состояния 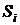 в любое другое
в любое другое 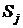 не зависит от того, когда и как система пришла в состояние
не зависит от того, когда и как система пришла в состояние 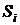 .
.
Марковскую непрерывную цепь называют "процессом гибели и размножения", если её граф состояний можно представить в виде вытянутой цепочки, в которой каждое из средних состояний связано прямой и обратной связью с каждым из соседних состояний, а крайние состояния – только с одним соседним состоянием. Этому определению соответствует рис. 16.1.
В установившемся режиме для состояния  алгебраическое уравнение академика Колмогорова можно записать в виде
алгебраическое уравнение академика Колмогорова можно записать в виде

а для состояния 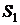 как
как
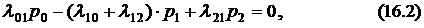
или после преобразования с учётом (16.1)

Составляя уравнение для некоторого состояния с учётом преобразования, аналогичного проделанному с формулами (16.1) и (16.2), получаем систему алгебраических уравнений



. . . . . . . . . . . . .

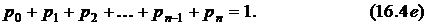
Последовательной заменой переменных, выражая вероятности состояний через 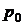 , систему уравнений (16.4) можно преобразовать к виду:
, систему уравнений (16.4) можно преобразовать к виду:

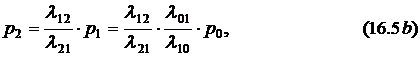
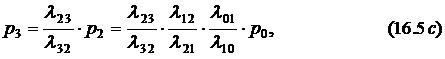
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
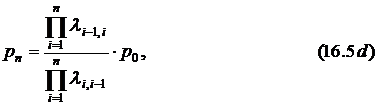
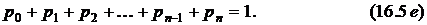
Подставляя выражения вероятностей в последнее уравнение системы, находим
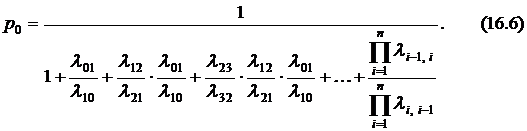
Теперь можно выразить через 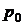 вероятности всех других состояний системы "гибели-размножения".
вероятности всех других состояний системы "гибели-размножения".
В частном случае, когда интенсивность отказов  постоянна, а СМО имеет
постоянна, а СМО имеет  каналов с интенсивностью обслуживания
каналов с интенсивностью обслуживания 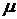 одной заявки одним каналом, КМО можно представить в виде графа (рис. 16.2). Здесь индекс у обозначения состояния
одной заявки одним каналом, КМО можно представить в виде графа (рис. 16.2). Здесь индекс у обозначения состояния 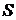 характеризует количество заявок в системе и, следовательно, количество занятых каналов.
характеризует количество заявок в системе и, следовательно, количество занятых каналов.

Рис. 16.2. Многоканальная СМО с отказами
Обозначив через 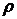 отношение
отношение 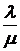 , получим с учётом формул (16.5) и (16.6)
, получим с учётом формул (16.5) и (16.6)
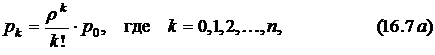
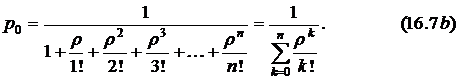
Эти выражения носят название формул Эрланга.
КМО характеризуют:
– вероятностью отказа 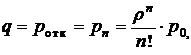
– относительной пропускной способностью 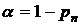 ,
,
– абсолютной пропускной способностью 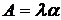 ,
,
– средним числом занятых каналов 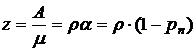 ,
,
– удельными затратами 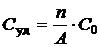 , то есть средними затратами на одну заявку при создании КМО, где
, то есть средними затратами на одну заявку при создании КМО, где 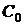 – стоимость одного канала.
– стоимость одного канала.
При 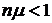 максимальная относительная пропускная способность
максимальная относительная пропускная способность 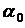 не может превышать величину
не может превышать величину 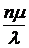 . При
. При 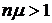 значение
значение 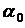 равно единице, то есть могут быть обслужены все заявки.
равно единице, то есть могут быть обслужены все заявки.
Под относительной пропускной способностью КМО можно понимать относительную величину исправных устройств среди всех имеющихся.
Пример.
Дано:  – интенсивность потока заявок,
– интенсивность потока заявок, 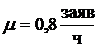 – интенсивность потока обслуживания заявок одним каналом КМО.
– интенсивность потока обслуживания заявок одним каналом КМО.
Найти основные характеристики одноканальной, двухканальной и трёхканальной СМО с отказами.
Найдём отношение интенсивностей потоков: 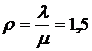 .
.
Решение: используя вышеприведённые уравнения, получим основные характеристики СМО (табл. 16.1).
Таблица 16.1
СМО с отказами
Характеристики СМО  , , 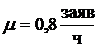 , , 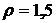 | Количество каналов | ||
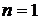 | 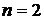 | 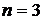 | |
Вероятности состояний: р 0 р 1 р 2 р 3 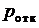 – вероятность отказа – вероятность отказа 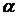 – относит. кол-во исправных устройств – относит. кол-во исправных устройств 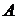 – абсолютная пропускная спос-сть, заяв/ч – абсолютная пропускная спос-сть, заяв/ч 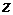 – среднее число занятых каналов – среднее число занятых каналов 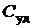 – удельные затраты на одну заявку – удельные затраты на одну заявку | 0,40 0,60 – – 0,60 0,40 0,48 0,60 2,08 | 0.2759 0,4138 0,3103 – 0,3103 0,6897 0,8276 1,0345 2,4167 | 0,2388 0,3582 0,2687 0,1343 0,1343 0,8657 1,0388 1,2985 2,8879 |
В данном примере интенсивность потока заявок взята в полтора раза больше интенсивности обслуживания одним каналом. Поэтому в одноканальной СМО относительное количество исправных устройств невелико и составляет всего 40%.
Из таблицы следует, что с ростом числа каналов процент исправных устройств также возрастает. Однако даже у трёхканальной СМО почти 24 процента времени все каналы свободны. Это можно объяснить случайным характером как поступления заявок, так и времени обслуживания каждой заявки.
КМО с ожиданием
Примерами комплексов массового обслуживания с ожиданием являются, например, телеателье и радиоремонтные мастерские, когда поступающие заявки на ремонт отказавшего устройства ставятся в очередь на обслуживание, если на момент поступления заявки мастера заняты ремонтом ранее поступивших заявок.
Различают СМО с ограниченной и неограниченной очередью.
Рассмотрим КМО из  -канальной СМО с ожиданием ("с очередью"), на которую поступает поток заявок с постоянной интенсивностью
-канальной СМО с ожиданием ("с очередью"), на которую поступает поток заявок с постоянной интенсивностью  . Интенсивность обслуживания заявки одним каналом обозначим через
. Интенсивность обслуживания заявки одним каналом обозначим через 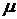 , а количество мест в очереди – через
, а количество мест в очереди – через  (рис. 16.3). Индексы около обозначений состояний
(рис. 16.3). Индексы около обозначений состояний 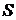 характеризуют количество заявок в системе.
характеризуют количество заявок в системе.
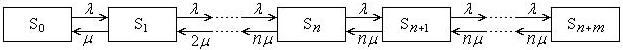
Рис. 16.3. Граф состояний многоканальной СМО с ожиданием
В состоянии  система свободна, заявок нет, "каналы" не заняты обслуживанием (ремонтом).
система свободна, заявок нет, "каналы" не заняты обслуживанием (ремонтом).
В состоянии 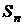 все каналы заняты, очередь отсутствует.
все каналы заняты, очередь отсутствует.
Начиная с состояния 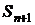 , в системе появляется очередь, причём второе слагаемое в индексе характеризует количество заявок, находящихся в очереди. Наличие очереди свидетельствует о том, что все каналы заняты обслуживанием заявок.
, в системе появляется очередь, причём второе слагаемое в индексе характеризует количество заявок, находящихся в очереди. Наличие очереди свидетельствует о том, что все каналы заняты обслуживанием заявок.
Пока очереди нет интенсивность перехода в предыдущее состояние возрастает с увеличением номера состояния от 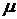 до максимальной величины
до максимальной величины 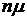 . После этого интенсивность обслуживания остаётся постоянной и максимально возможной.
. После этого интенсивность обслуживания остаётся постоянной и максимально возможной.
Для состояний от  до
до 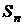 остаются справедливыми формулы (16.7). Продолжая вывод уравнений по схеме "гибели-размножения" (16.3) для состояний от
остаются справедливыми формулы (16.7). Продолжая вывод уравнений по схеме "гибели-размножения" (16.3) для состояний от 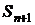 до
до 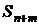 , получаем
, получаем

Выражая вероятности последующего состояния через предыдущее, преобразуем эту систему уравнений к виду
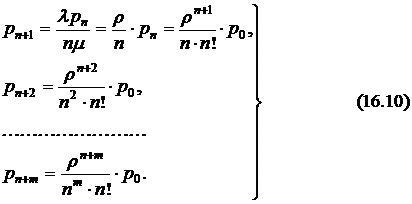
Используя нормировочное уравнение 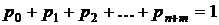 , получим
, получим
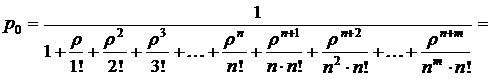
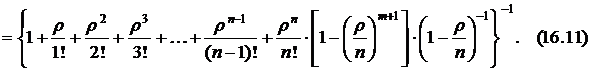
Таким образом, найдено выражение вероятности 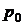 нахождения системы в состоянии
нахождения системы в состоянии  через известные величины
через известные величины 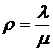 ,
,  и найдены выражения вероятностей всех остальных состояний через
и найдены выражения вероятностей всех остальных состояний через 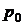 .
.
КМО с ожиданием, кроме таких показателей как
– вероятность отказа 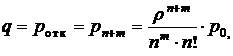
– относительная пропускная способность 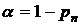 ,
,
– абсолютная пропускная способность 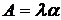 ,
,
– среднее число занятых каналов 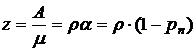 ,
,
– удельные затраты 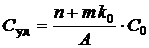 , то есть средние затраты на одну заявку при создании КМО, где
, то есть средние затраты на одну заявку при создании КМО, где 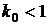 – относительные по сравнению с каналом затраты на создание одного места в очереди,
– относительные по сравнению с каналом затраты на создание одного места в очереди, 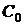 – стоимость затрат на создание одного канала,
– стоимость затрат на создание одного канала,
дополнительно характеризуют
– средним числом заявок в очереди
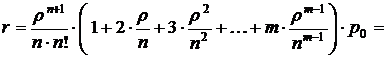
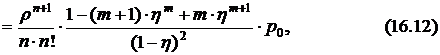
где 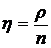 .
.
– средним числом заявок, находящихся в системе: 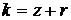 (16.13),
(16.13),
– средним временем ожидания
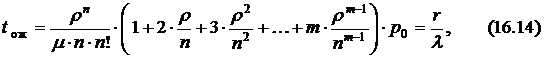
– средним временем обслуживания в канале 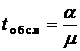 , (16.15)
, (16.15)
– средним временем пребывания заявки в системе
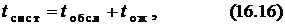
– увеличением относительной пропускной способности СМО за счёт введения очереди с ограниченным количеством мест в ней
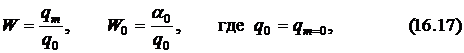
и некоторыми другими показателями.
Организация очереди оправдывает себя с экономической точки зрения, если затраты на создание одного места не превышают 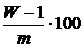 процентов от стоимости
процентов от стоимости 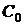 .
.
Пример.
Дано:  – интенсивность потока заявок,
– интенсивность потока заявок, 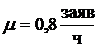 – интенсивность потока обслуживания заявок одним каналом КМО.
– интенсивность потока обслуживания заявок одним каналом КМО.
Найти основные характеристики одноканальной, двухканальной и трёхканальной СМО с отказами.
Найдём отношение интенсивностей потоков: 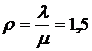 .
.
Решение: используя вышеприведённые уравнения, получим основные характеристики СМО (табл. 16.2 ÷ 16.4).
Из табл. 16.2 следует, что наибольшие вероятности имеют состояния СМО, когда все места в очереди заняты. Это вполне логично, так как относительная пропускная способность низкая: 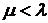 и
и 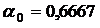 .
.
Таблица 16.2
