Логарифмически нормальный закон распределения

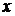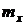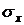Случайную величину называют распределённой по логарифмически нормальному закону с параметрами и , если её десятичный логарифм 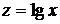распределен по нормальному закону. Плотность распределения в этом случае имеет вид (рис. 5.4) [1, 4]

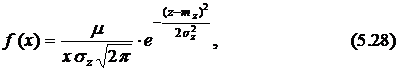
где .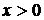

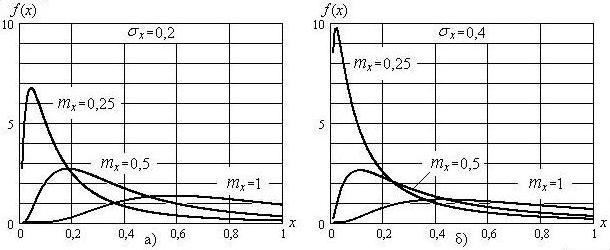
Рис. 5.4. Плотность распределения непрерывной случайной величины по логарифмически нормальному закону

Кроме того, здесь обозначено: ;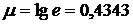

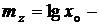математическое ожидание случайной величины ,

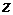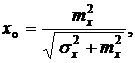
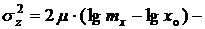дисперсия случайной величины ,

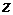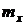и 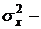математическое ожидание и дисперсия случайной величины 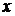соответственно.

Логарифмически нормальный закон распределения удобно использовать как распределение износовых отказов, когда 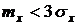[1]. Важным достоинством этого распределения является то, что 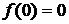. Так как обычно под величиной 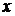понимается время 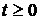, то вероятность отказа в интервале времени от 0 до 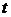можно рассчитать по формуле

Лекция 6. «Общие принципы повышения надёжности. Резервирование»

План лекции:

Возможные причины низкой надёжности РЭУ

Методы повышения надёжности РЭУ

Резервирование

Общее нагруженное резервирование без восстановления

Возможные причины низкой надёжности РЭУ

Основные причины низкой надёжности радиоэлектронных устройств связаны с недостатком наших знаний, опыта и времени, отводимого на разработку. С инженерной точки зрения низкая надёжность является, как правило, следствием конструкторских, технологических и эксплуатационных ошибок [4].

К конструкторским ошибкам относят:

– неоптимальный выбор принципиальной электрический схемы с точки зрения выполнения возложенных на неё функций,

– неоптимальный выбор комплектующих элементов, не в полной мере учитывающий их физико-химические свойства, электрические, тепловые, электромагнитные, механические и другие режимы работы элементов,

– неоптимальный выбор исходных материалов, не полностью учитывающий условия работы РЭУ в целом,

– неоптимальный выбор допусков на комплектующие элементы,

– недостаточная стабилизация режимов работы узлов и блоков,

– недостаточная эффективность выбранных средств и методов защиты РЭУ от дестабилизирующих факторов,

– технические ошибки в чертежах и документах и др.

К технологическим ошибкам относят:

– использование низкокачественных комплектующих элементов,

– применение низкокачественных материалов,

– несовершенство выбранных технологических процессов,

– несоблюдение технологических режимов,

– несовершенство технологического оборудования,

– недостаточный уровень автоматизации производственных процессов,

– нарушение санитарно-гигиенических норм производства и т.д.

Эксплуатационной ошибкой является использование РЭУ в несоответствующих техническим условиям режимах эксплуатации.