Представление отношений диаграммами
Пусть r Í А 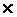 B. Это отношение между элементами множеств А и B. Если множества A и B счетные, то их можно представить на плоскости множествами точек из двух непересекающихся областей, обозначаемых как A и B. Если (a, b)
B. Это отношение между элементами множеств А и B. Если множества A и B счетные, то их можно представить на плоскости множествами точек из двух непересекающихся областей, обозначаемых как A и B. Если (a, b) 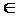 r, то точки, соответствующие a и b, соединяются ориентированной дугой. Такое представление аналогично диаграммам для отображений. При этом для диаграмм отношений допускается как многозначность связи элементов A с элементами B, так и отсутствие связей.
r, то точки, соответствующие a и b, соединяются ориентированной дугой. Такое представление аналогично диаграммам для отображений. При этом для диаграмм отношений допускается как многозначность связи элементов A с элементами B, так и отсутствие связей.
В случаях, когда в отношение входит много пар из А ´ B, или отношение обладает специальными свойствами изображение диаграммы отношения становится сложным для понимания. Поэтому могут применяться специальные правила уменьшения числа отображаемых связей. Например, в некоторых случаях не отображаются связи между элементами, для которых существует возможность связывания соответствующих им вершин с помощью последовательности уже изображенных дуг, проходящих через другие вершины.
Табличное задание отношений
Если множества A и B являются конечными и A = {a1,..., am}, B= {b1, ... , bn}, то всякое отношение r Í А 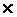 B можно представить таблицей, состоящей из m строк и n столбцов, имеющей следующий вид:
B можно представить таблицей, состоящей из m строк и n столбцов, имеющей следующий вид:
| b1 bj bn | |
| a1 ai am | . . . . . . . . si,j . . . . . . . . . |
В этой таблице значение всякого элемента si,j определяется соотношением:
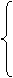 1, если (ai, bj)Îr
1, если (ai, bj)Îr
si,j =
0, если (ai, bj)Ïr.
Всякая заполненная нулями и единицами таблица, состоящая из m строк и n столбцов, представляет некоторое отношение на множествах A и B, составленное из всех таких пар (ai, bj), для которых si,j = 1.
Определенное соотношение таблиц и отношений на множествах является биективным. Табличное представление отношений удобно для программной реализации алгоритмов решения задач, связанных с отношениями.
ОПЕРАЦИИ НАД ОТНОШЕНИЯМИ
ОПРЕДЕЛЕНИЕ
Пусть 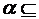 А
А 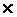 B и
B и 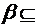 B
B 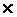 C. Тогда отношение
C. Тогда отношение 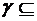 А
А 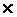 C называется произведением отношений
C называется произведением отношений  и
и  , если выполнено условие:
, если выполнено условие:
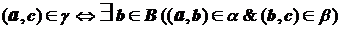 .
.
Произведение двух отношений  и
и  обозначается как
обозначается как  ◦
◦  или как
или как 
 . Произведение отношений обладает свойством ассоциативности.
. Произведение отношений обладает свойством ассоциативности.
ТЕОРЕМА 3.1
Если заданы отношения 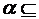 А
А 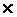 B,
B, 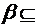 B
B 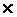 C,
C, 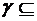 С
С 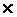 D, то справедливо равенство
D, то справедливо равенство  ◦(
◦(  ◦
◦ 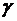 ) = (
) = (  ◦
◦  )◦
)◦ 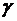 .
.
Доказательство
1. Покажем, что  (
( 
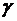 )
) 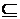 (
( 
 )
) 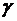 .
.
Действительно, пусть (a, d) 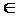
 (
( 
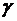 ), т.е. существует b такое, что a a b и b(
), т.е. существует b такое, что a a b и b( 
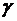 )d. Тогда существует такое с, что b
)d. Тогда существует такое с, что b  с и с
с и с 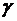 d. Поэтому a(
d. Поэтому a( 
 )с. Это означает, что a((
)с. Это означает, что a(( 
 )
) 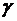 )d. Следовательно, справедливо включение
)d. Следовательно, справедливо включение  (
( 
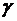 )
) 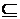 (
( 
 )
) 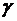 .
.
2. Покажем, что ( 
 )
) 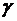 )
) 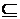
 (
( 
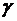 ).
).
Пусть (a, d) 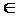 (
( 
 )
) 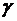 . Тогда существует такое с, что
. Тогда существует такое с, что
a ( 
 )с и с
)с и с 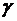 d. Поэтому найдется такой элемент b, для которого справедливы соотношения: a
d. Поэтому найдется такой элемент b, для которого справедливы соотношения: a  b и b
b и b  с. Поэтому b(
с. Поэтому b( 
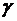 )d, т.е. a
)d, т.е. a  (
( 
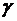 )d.
)d.
Следовательно, имеет место включение множеств:
( 
 )
) 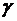
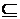
 (
( 
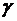 ) .
) .
Значит,  (
( 
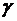 ) = (
) = ( 
 )
) 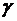 .
.
Доказательство окончено.
Заметим, что произведение отношений является аналогом произведения отображений. Для того, чтобы увидеть такую аналогию достаточно сопоставить произвольной функции f: A® B отношение {(x, f(x)) ½ xÎA}, которое называется графиком этой функции. Тогда, если отображение h является произведением отображений g и f, то график h -произведением графиков для g и f.
Рассмотрим пример. Пусть A - это множество людей, а C - множество городов.
Пусть на этих множествах определены отношения:
 Í A ´ A - отношение знакомства людей, а
Í A ´ A - отношение знакомства людей, а  Í A ´ B - отношение проживания в некотором городе. То есть, если справедливо соотношение aab, то это означает, что a знает b. Поэтому отношение
Í A ´ B - отношение проживания в некотором городе. То есть, если справедливо соотношение aab, то это означает, что a знает b. Поэтому отношение 
 - представляет такие связи между людьми игородами, для которого справедливость соотношения a(
- представляет такие связи между людьми игородами, для которого справедливость соотношения a( 
 )c означает, что a имеет знакомого в городе c. При этом точное знание конкретного человека, связывающего a и c не требуется, поскольку для выполнимости отношения abac важно лишь его существование.
)c означает, что a имеет знакомого в городе c. При этом точное знание конкретного человека, связывающего a и c не требуется, поскольку для выполнимости отношения abac важно лишь его существование.
ОПРЕДЕЛЕНИЕ
Пусть 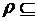 А
А 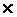 B. Тогда отношение {(y, x)|(x, y)Îr} называется отношением, обратным к отношению r.
B. Тогда отношение {(y, x)|(x, y)Îr} называется отношением, обратным к отношению r.
Для обозначения отношения, обратного к r, применяется запись r-1.
Понятие обращения отношений есть обобщение понятия обратного отображения. При этом обратное отношение всегда существует. Поскольку (r-1)-1= r, то отношения и их обращения находятся в биективной зависимости. Поэтому обращение всякого отношения порождает в общем случае новое отношение, которое совпадает с ним с точностью до простого преобразования.
Например, рассмотрим отношение управления людьми руководит Í A ´ A, где A - множество людей, определяемое соотношением: arb Û a руководит b.
Тогда отношение, обратное к отношению руководит, можно назвать словом руководим. Такое название соответствует содержательному смыслу обратной связи между b и a.
Понятие отношения может быть обобщено на произвольное конечное семейство множеств А1, .., Аk следующим образом.
Отношением на произвольном числе множеств А1, ... , Аk является всякое множество 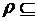 А1
А1 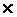 ...
... 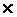 Аk. Однако отношения на парах множеств являются практически наиболее часто используемыми отношениями. Во многих случаях через такие отношения, с помощью специальных комбинаций отношений, могут выражаться отношения над более чем двумя множествами.
Аk. Однако отношения на парах множеств являются практически наиболее часто используемыми отношениями. Во многих случаях через такие отношения, с помощью специальных комбинаций отношений, могут выражаться отношения над более чем двумя множествами.
